সিঁড়ি। এন্ট্রি গ্রুপ। উপকরণ। দরজা. তালা। ডিজাইন

এখানে আপনি পিরামিড এবং সম্পর্কিত সূত্র এবং ধারণা সম্পর্কে প্রাথমিক তথ্য পেতে পারেন। ইউনিফাইড স্টেট পরীক্ষার প্রস্তুতির জন্য তাদের সকলকে গণিতের শিক্ষকের সাথে অধ্যয়ন করা হয়।

একটি সমতল, একটি বহুভুজ বিবেচনা করুন , এটিতে শুয়ে আছে এবং একটি বিন্দু S, এতে শুয়ে নেই। এস কে বহুভুজের সমস্ত শীর্ষবিন্দুর সাথে সংযুক্ত করি। ফলে পলিহেড্রনকে পিরামিড বলা হয়। অংশগুলিকে পার্শ্ব পাঁজর বলা হয়। বহুভুজকে ভিত্তি বলা হয় এবং বিন্দু S হল পিরামিডের শীর্ষ। n সংখ্যার উপর নির্ভর করে, পিরামিডকে ত্রিভুজাকার (n=3), চতুর্ভুজাকার (n=4), পঞ্চভুজ (n=5) ইত্যাদি বলা হয়। একটি ত্রিভুজাকার পিরামিডের একটি বিকল্প নাম টেট্রাহেড্রন. পিরামিডের উচ্চতা হল তার উপর থেকে ভিত্তির সমতলে অবতরণ করা লম্ব।

একটি পিরামিড নিয়মিত যদি বলা হয় একটি নিয়মিত বহুভুজ, এবং পিরামিডের উচ্চতার ভিত্তি (লম্বের ভিত্তি) হল এর কেন্দ্র।

শিক্ষকের মন্তব্য:
"নিয়মিত পিরামিড" এবং "নিয়মিত টেট্রাহেড্রন" এর ধারণাগুলিকে বিভ্রান্ত করবেন না। একটি নিয়মিত পিরামিডে, পাশের প্রান্তগুলি অগত্যা বেসের প্রান্তের সমান হয় না, তবে একটি নিয়মিত টেট্রাহেড্রনে, সমস্ত 6টি প্রান্ত সমান। এটা তার সংজ্ঞা। এটা প্রমাণ করা সহজ যে সমতা বোঝায় যে বহুভুজের কেন্দ্র P মিলে যায় একটি বেস উচ্চতা সহ, তাই একটি নিয়মিত টেট্রাহেড্রন একটি নিয়মিত পিরামিড।

একটি apothem কি?
পিরামিডের apothem হল এর পাশের মুখের উচ্চতা। যদি পিরামিড নিয়মিত হয়, তাহলে এর সমস্ত অপোথেম সমান। বিপরীত সত্য নয়।

তার পরিভাষা সম্পর্কে একজন গণিতের শিক্ষক: পিরামিডের সাথে 80% কাজ দুটি ধরণের ত্রিভুজের মাধ্যমে নির্মিত হয়:
1) apothem SK এবং উচ্চতা SP ধারণকারী
2) পার্শ্বীয় প্রান্ত SA এবং এর অভিক্ষেপ PA ধারণ করে

এই ত্রিভুজগুলির রেফারেন্সগুলি সরল করার জন্য, গণিতের শিক্ষকের পক্ষে তাদের প্রথমটিকে কল করা আরও সুবিধাজনক। apothemal, এবং দ্বিতীয় ব্যয়বহুল. দুর্ভাগ্যবশত, আপনি কোনো পাঠ্যপুস্তকে এই পরিভাষাটি পাবেন না এবং শিক্ষককে এটি একতরফাভাবে প্রবর্তন করতে হবে।

পিরামিডের আয়তনের সূত্র:
1) , পিরামিডের ভিত্তির ক্ষেত্রফল কোথায় এবং পিরামিডের উচ্চতা কোথায়
2) , খোদাই করা গোলকের ব্যাসার্ধ কোথায় এবং পিরামিডের মোট পৃষ্ঠের ক্ষেত্রফল।
3) , যেখানে MN হল যেকোনো দুটি ক্রসিং প্রান্তের মধ্যবর্তী দূরত্ব এবং চারটি অবশিষ্ট প্রান্তের মধ্যবিন্দু দ্বারা গঠিত সমান্তরালগ্রামের ক্ষেত্রফল।

পিরামিডের উচ্চতার ভিত্তির বৈশিষ্ট্য:

বিন্দু P (চিত্র দেখুন) পিরামিডের গোড়ায় খোদাই করা বৃত্তের কেন্দ্রের সাথে মিলে যায় যদি নিম্নলিখিত শর্তগুলির মধ্যে একটি পূরণ করা হয়:
1) সমস্ত apothems সমান
2) সমস্ত পাশের মুখগুলি সমানভাবে বেসের দিকে ঝুঁকে আছে
3) সমস্ত অ্যাপোথেম পিরামিডের উচ্চতায় সমানভাবে ঝুঁকে আছে
4) পিরামিডের উচ্চতা সব দিকের মুখের দিকে সমানভাবে ঝুঁকে আছে

গণিত শিক্ষকের মন্তব্য: দয়া করে মনে রাখবেন যে সমস্ত পয়েন্টে একটি জিনিস মিল রয়েছে সাধারণ সম্পত্তি: একভাবে বা অন্যভাবে, পার্শ্বীয় মুখগুলি সর্বত্র জড়িত থাকে (অ্যাপোথেমগুলি তাদের উপাদান)। অতএব, গৃহশিক্ষক একটি কম সুনির্দিষ্ট, কিন্তু শেখার জন্য আরও সুবিধাজনক, সূত্র দিতে পারেন: বিন্দু P খোদাই করা বৃত্তের কেন্দ্রের সাথে মিলে যায়, পিরামিডের ভিত্তি, যদি এর পার্শ্বীয় মুখগুলি সম্পর্কে কোনও সমান তথ্য থাকে। এটি প্রমাণ করার জন্য, এটি দেখানো যথেষ্ট যে সমস্ত apothem ত্রিভুজ সমান।

বিন্দু P পিরামিডের গোড়ার কাছাকাছি একটি বৃত্তের কেন্দ্রের সাথে মিলে যায় যদি তিনটি শর্তের মধ্যে একটি সত্য হয়:
1) সমস্ত পাশের প্রান্ত সমান
2) সমস্ত পাশের পাঁজর সমানভাবে বেসের দিকে ঝুঁকে আছে
3) সমস্ত পাশের পাঁজর সমানভাবে উচ্চতার দিকে ঝুঁকে আছে

এই ভিডিও টিউটোরিয়াল ব্যবহারকারীদের পিরামিড থিম সম্পর্কে ধারণা পেতে সাহায্য করবে। সঠিক পিরামিড। এই পাঠে আমরা পিরামিডের ধারণার সাথে পরিচিত হব এবং এর একটি সংজ্ঞা দেব। আসুন একটি নিয়মিত পিরামিড কী এবং এর কী বৈশিষ্ট্য রয়েছে তা বিবেচনা করা যাক। তারপরে আমরা একটি নিয়মিত পিরামিডের পার্শ্বীয় পৃষ্ঠ সম্পর্কে উপপাদ্য প্রমাণ করি।

এই পাঠে আমরা পিরামিডের ধারণার সাথে পরিচিত হব এবং এর একটি সংজ্ঞা দেব।

একটি বহুভুজ বিবেচনা করুন ক 1 ক 2...একটি, যা α সমতল এবং বিন্দুতে অবস্থিত পৃ, যা α সমতলে থাকে না (চিত্র 1)। এর বিন্দু সংযোগ করা যাক পৃচূড়া সহ A 1, A 2, A 3, … একটি. আমরা পেতে nত্রিভুজ: A 1 A 2 R, A 2 A 3 Rএবং তাই

সংজ্ঞা. পলিহেড্রন RA 1 A 2 ...A n, গঠিত n-বর্গক্ষেত্র ক 1 ক 2...একটিএবং nত্রিভুজ RA 1 A 2, RA 2 A 3 …RA n A n-1 বলা হয় n- কয়লা পিরামিড। ভাত। 1.

ভাত। 1

একটি চতুর্ভুজাকার পিরামিড বিবেচনা করুন PABCD(চিত্র 2)।

আর- পিরামিডের শীর্ষে।

এ বি সি ডি- পিরামিডের ভিত্তি।

রা- পাশের পাঁজর।

এবি- ভিত্তি পাঁজর।

বিন্দু থেকে আরএর লম্ব ড্রপ করা যাক আরএনবেস সমতলে এ বি সি ডি. অঙ্কিত লম্ব হল পিরামিডের উচ্চতা।

ভাত। 2

পিরামিডের পূর্ণ পৃষ্ঠটি পার্শ্বীয় পৃষ্ঠ, অর্থাৎ সমস্ত পার্শ্বীয় মুখের ক্ষেত্রফল এবং ভিত্তির ক্ষেত্রফল নিয়ে গঠিত:

S পূর্ণ = S পার্শ্ব + S প্রধান

একটি পিরামিডকে সঠিক বলা হয় যদি:

• এর ভিত্তি একটি নিয়মিত বহুভুজ;
• পিরামিডের উপরের অংশটিকে ভিত্তির কেন্দ্রের সাথে সংযুক্ত করে তার উচ্চতা।

একটি নিয়মিত চতুর্ভুজাকার পিরামিডের উদাহরণ ব্যবহার করে ব্যাখ্যা

একটি নিয়মিত চতুর্ভুজাকার পিরামিড বিবেচনা করুন PABCD(চিত্র 3)।

আর- পিরামিডের শীর্ষে। পিরামিডের ভিত্তি এ বি সি ডি - নিয়মিত চতুর্ভুজ, অর্থাৎ একটি বর্গক্ষেত্র। ডট সম্পর্কিত, কর্ণগুলির ছেদ বিন্দু, বর্গক্ষেত্রের কেন্দ্র। মানে, ROপিরামিডের উচ্চতা।

ভাত। 3

ব্যাখ্যা: সঠিকভাবে nএকটি ত্রিভুজে, খোদাই করা বৃত্তের কেন্দ্র এবং বৃত্তের কেন্দ্র একত্রিত হয়। এই কেন্দ্রটিকে বহুভুজের কেন্দ্র বলা হয়। কখনও কখনও তারা বলে যে শীর্ষবিন্দুটি কেন্দ্রে অভিক্ষিপ্ত হয়।

তার শীর্ষবিন্দু থেকে আঁকা একটি নিয়মিত পিরামিডের পার্শ্বীয় মুখের উচ্চতা বলা হয় apothemএবং মনোনীত করা হয় জ ক.

1. একটি নিয়মিত পিরামিডের সমস্ত পার্শ্বীয় প্রান্ত সমান;

2. পাশের মুখগুলি সমান সমদ্বিবাহু ত্রিভুজ।

আমরা একটি নিয়মিত চতুর্ভুজাকার পিরামিডের উদাহরণ ব্যবহার করে এই বৈশিষ্ট্যগুলির একটি প্রমাণ দেব।

দেওয়া: PABCD- নিয়মিত চতুর্ভুজাকার পিরামিড,

এ বি সি ডি- বর্গক্ষেত্র,

RO- পিরামিডের উচ্চতা।

প্রমাণ করুন:

1. RA = PB = RS = PD

2.∆ABP = ∆BCP =∆CDP =∆DAP চিত্র দেখুন। 4.

ভাত। 4

প্রমাণ.

RO- পিরামিডের উচ্চতা। অর্থাৎ সোজা ROসমতলে লম্ব এবিসি, এবং তাই সরাসরি JSC, VO, SOএবং DOএটা শুয়ে আছে. তাই ত্রিভুজ ROA, ROV, ROS, ROD- আয়তক্ষেত্রাকার.

একটি বর্গক্ষেত্র বিবেচনা করুন এ বি সি ডি. একটি বর্গক্ষেত্রের বৈশিষ্ট্য থেকে এটি অনুসরণ করে AO = VO = CO = DO.

তারপর সমকোণী ত্রিভুজ ROA, ROV, ROS, RODপা RO- সাধারণ এবং পা JSC, VO, SOএবং DOসমান, যার মানে এই ত্রিভুজ দুটি পাশে সমান। ত্রিভুজগুলির সমতা থেকে বিভাগগুলির সমতা অনুসরণ করে, RA = PB = RS = PD.পয়েন্ট 1 প্রমাণিত হয়েছে।

সেগমেন্ট এবিএবং সূর্যসমান কারণ তারা একই বর্গক্ষেত্রের বাহু, RA = PB = RS. তাই ত্রিভুজ এভিআরএবং ভিএসআর -সমদ্বিবাহু এবং তিন দিকে সমান।

একইভাবে আমরা সেই ত্রিভুজগুলি খুঁজে পাই ABP, VCP, CDP, DAPসমদ্বিবাহু এবং সমান, অনুচ্ছেদ 2 এ প্রমাণ করা প্রয়োজন।

একটি নিয়মিত পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল বেস এবং অ্যাপোথেমের পরিধির অর্ধেক গুণফলের সমান:

এটি প্রমাণ করতে, আসুন একটি নিয়মিত ত্রিভুজাকার পিরামিড বেছে নেওয়া যাক।

দেওয়া: RAVS- নিয়মিত ত্রিভুজাকার পিরামিড।

AB = BC = AC.

RO- উচ্চতা।

প্রমাণ করুন: . চিত্র দেখুন। 5.

ভাত। 5

প্রমাণ।

RAVS- নিয়মিত ত্রিভুজাকার পিরামিড। এটাই এবি= AC = BC. দিন সম্পর্কিত- ত্রিভুজের কেন্দ্র এবিসি, তারপর ROপিরামিডের উচ্চতা। পিরামিডের গোড়ায় একটি সমবাহু ত্রিভুজ রয়েছে এবিসি. লক্ষ্য করুন .

ত্রিভুজ RAV, RVS, RSA- সমান সমদ্বিবাহু ত্রিভুজ (সম্পত্তি দ্বারা)। একটি ত্রিভুজাকার পিরামিডের তিনটি মুখ রয়েছে: RAV, RVS, RSA. এর অর্থ হল পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল হল:

S side = 3S RAW

উপপাদ্য প্রমাণিত হয়েছে।

একটি নিয়মিত চতুর্ভুজাকার পিরামিডের গোড়ায় খোদিত একটি বৃত্তের ব্যাসার্ধ 3 মিটার, পিরামিডের উচ্চতা 4 মিটার। পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল নির্ণয় করুন।

দেওয়া: নিয়মিত চতুর্ভুজাকার পিরামিড এ বি সি ডি,

এ বি সি ডি- বর্গক্ষেত্র,

r= 3 মি,

RO- পিরামিডের উচ্চতা,

RO= 4 মি.

অনুসন্ধান: এস পাশ। চিত্র দেখুন। 6.

ভাত। 6

সমাধান.

প্রমাণিত উপপাদ্য অনুযায়ী, .

প্রথমে বেসের দিকটি খুঁজে বের করা যাক এবি. আমরা জানি যে একটি নিয়মিত চতুর্ভুজাকার পিরামিডের গোড়ায় খোদিত একটি বৃত্তের ব্যাসার্ধ 3 মিটার।

তারপর, মি.

বর্গক্ষেত্রের পরিধি নির্ণয় কর এ বি সি ডি 6 মিটারের পাশে:

একটি ত্রিভুজ বিবেচনা করুন বিসিডি. দিন এম- পাশের মাঝখানে ডিসি. কারণ সম্পর্কিত- মাঝখানে বিডি, যে (মি)

ত্রিভুজ ডিপিসি- সমদ্বিবাহু। এম- মাঝখানে ডিসি. এটাই, আরএম- মধ্যমা, এবং তাই ত্রিভুজের উচ্চতা ডিপিসি. তারপর আরএম- পিরামিড এর apothem.

RO- পিরামিডের উচ্চতা। তারপর, সোজা ROসমতলে লম্ব এবিসি, এবং তাই সরাসরি ওম, এটা শুয়ে. আসুন apothem খুঁজে বের করা যাক আরএমথেকে সঠিক ত্রিভুজ রম.

এখন আমরা খুঁজে পেতে পারেন পাশর্্বীয় পৃষ্ঠপিরামিড:

উত্তর: 60 m2।

একটি নিয়মিত ত্রিভুজাকার পিরামিডের গোড়ার চারপাশে ঘেরা বৃত্তের ব্যাসার্ধ m এর সমান। পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল হল 18 m 2। এপোথেমের দৈর্ঘ্য খুঁজুন।

দেওয়া: এবিসিপি- নিয়মিত ত্রিভুজাকার পিরামিড,

AB = BC = SA,

আর= মি,

S পাশ = 18 m2।

অনুসন্ধান: চিত্র দেখুন। 7.

ভাত। 7

সমাধান.

সমকোণী ত্রিভুজে এবিসিপরিধিকৃত বৃত্তের ব্যাসার্ধ দেওয়া আছে। আসুন একটি দিক খুঁজে বের করা যাক এবিসাইনের নিয়ম ব্যবহার করে এই ত্রিভুজ।

একটি নিয়মিত ত্রিভুজ (m) এর দিক জেনে আমরা এর পরিধি খুঁজে পাই।

উপপাদ্য দ্বারা একটি নিয়মিত পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল, যেখানে জ ক- পিরামিড এর apothem. তারপর:

উত্তর: 4 মি.

সুতরাং, আমরা একটি পিরামিড কি, একটি নিয়মিত পিরামিড কি তা দেখেছি এবং আমরা একটি নিয়মিত পিরামিডের পার্শ্বীয় পৃষ্ঠ সম্পর্কে উপপাদ্য প্রমাণ করেছি। পরবর্তী পাঠে আমরা ছেঁটে যাওয়া পিরামিডের সাথে পরিচিত হব।

গ্রন্থপঞ্জি

1. জ্যামিতি. গ্রেড 10-11: সাধারণ শিক্ষা প্রতিষ্ঠানের শিক্ষার্থীদের জন্য পাঠ্যপুস্তক (মৌলিক এবং প্রোফাইল স্তর) / I. M. Smirnova, V. A. Smirnov। - 5ম সংস্করণ। এবং অতিরিক্ত - এম.: মেমোসিন, 2008। - 288 পি।: অসুস্থ।
2. জ্যামিতি. 10-11 গ্রেড: সাধারণ শিক্ষার জন্য পাঠ্যপুস্তক শিক্ষা প্রতিষ্ঠান/ শারিগিন আই.এফ. - এম.: বাস্টার্ড, 1999। - 208 পি.: অসুস্থ।
3. জ্যামিতি. গ্রেড 10: সাধারণ শিক্ষা প্রতিষ্ঠানের জন্য পাঠ্যপুস্তক যা গণিতের গভীর ও বিশেষায়িত অধ্যয়ন/ই। ভি. পোটোস্কুয়েভ, এল. আই. জভালিচ। - ৬ষ্ঠ সংস্করণ, স্টেরিওটাইপ। - এম.: বাস্টার্ড, 008. - 233 পি.: অসুস্থ।

1. ইন্টারনেট পোর্টাল "ইয়াক্লাস" ()
2. ইন্টারনেট পোর্টাল "শিক্ষাগত ধারণার উত্সব" সেপ্টেম্বরের প্রথম" ()
3. ইন্টারনেট পোর্টাল "Slideshare.net" ()

বাড়ির কাজ

1. একটি নিয়মিত বহুভুজ কি একটি অনিয়মিত পিরামিডের ভিত্তি হতে পারে?
2. প্রমাণ করুন যে একটি নিয়মিত পিরামিডের বিচ্ছিন্ন প্রান্তগুলি লম্ব।
3. একটি নিয়মিত চতুর্ভুজাকার পিরামিডের গোড়ার পাশের ডাইহেড্রাল কোণের মান নির্ণয় করুন যদি পিরামিডের এপোথেম তার ভিত্তির পাশের সমান হয়।
4. RAVS- নিয়মিত ত্রিভুজাকার পিরামিড। পিরামিডের গোড়ায় ডিহেড্রাল কোণের রৈখিক কোণ তৈরি করুন।

• apothem- একটি নিয়মিত পিরামিডের পাশের মুখের উচ্চতা, যা এটির শীর্ষবিন্দু থেকে আঁকা হয় (অতিরিক্ত, অ্যাপোথেমটি লম্বের দৈর্ঘ্য, যা নিয়মিত বহুভুজের মাঝখানে থেকে এর একটি দিকে নামানো হয়);
• পাশের মুখ (ASB, BSC, CSD, DSA) - শীর্ষবিন্দুতে মিলিত ত্রিভুজ;
• পার্শ্বীয় পাঁজর ( এএস , বি.এস. , সি.এস. , ডি এস. ) - পাশের মুখের সাধারণ দিকগুলি;
• পিরামিডের শীর্ষে (t. S) - একটি বিন্দু যা পাশের পাঁজরকে সংযুক্ত করে এবং যা বেসের সমতলে থাকে না;
• উচ্চতা ( তাই ) - পিরামিডের শীর্ষ দিয়ে তার বেসের সমতলে আঁকা একটি লম্ব অংশ (এই ধরনের একটি অংশের শেষগুলি পিরামিডের শীর্ষ এবং লম্বের ভিত্তি হবে);
• পিরামিডের তির্যক অংশ- পিরামিডের একটি অংশ যা বেসের উপরের এবং তির্যক দিয়ে যায়;
• ভিত্তি (এ বি সি ডি) - একটি বহুভুজ যা পিরামিডের শীর্ষবিন্দুর অন্তর্গত নয়।

পিরামিডের বৈশিষ্ট্য।

1. যখন সমস্ত পাশের প্রান্ত একই আকারের হয়, তখন:

• পিরামিডের ভিত্তির কাছাকাছি একটি বৃত্ত বর্ণনা করা সহজ, এবং পিরামিডের শীর্ষটি এই বৃত্তের কেন্দ্রে প্রক্ষিপ্ত হবে;
• পাশের পাঁজরগুলি বেসের সমতলের সাথে সমান কোণ তৈরি করে;
• তদুপরি, বিপরীতটিও সত্য, অর্থাৎ যখন পার্শ্বীয় পাঁজরগুলি ভিত্তির সমতলের সাথে তৈরি হয় সমান কোণ, অথবা যখন পিরামিডের ভিত্তির কাছে একটি বৃত্ত বর্ণনা করা যেতে পারে এবং পিরামিডের শীর্ষটি এই বৃত্তের কেন্দ্রে প্রক্ষিপ্ত হবে, যার অর্থ হল পিরামিডের সমস্ত পাশের প্রান্তগুলি একই আকারের।

2. যখন পাশের মুখগুলির একই মানের বেসের সমতলে প্রবণতার একটি কোণ থাকে, তখন:

• পিরামিডের ভিত্তির কাছাকাছি একটি বৃত্ত বর্ণনা করা সহজ, এবং পিরামিডের শীর্ষটি এই বৃত্তের কেন্দ্রে প্রক্ষিপ্ত হবে;
• পাশ মুখের উচ্চতা হয় সমান দৈর্ঘ্য;
• পাশের পৃষ্ঠের ক্ষেত্রফল বেসের পরিধির গুণফল এবং পাশের মুখের উচ্চতার সমান।

3. পিরামিডের চারপাশে একটি গোলক বর্ণনা করা যেতে পারে যদি পিরামিডের গোড়ায় একটি বহুভুজ থাকে যার চারপাশে একটি বৃত্ত বর্ণনা করা যায় (একটি প্রয়োজনীয় এবং যথেষ্ট শর্ত)। গোলকের কেন্দ্রটি প্লেনগুলির ছেদ বিন্দু হবে যা তাদের লম্ব পিরামিডের প্রান্তগুলির মধ্য দিয়ে যায়। এই উপপাদ্য থেকে আমরা উপসংহারে পৌঁছেছি যে একটি গোলককে যেকোনো ত্রিভুজাকার এবং যেকোনো নিয়মিত পিরামিডের চারপাশে বর্ণনা করা যেতে পারে।

4. পিরামিডের অভ্যন্তরীণ ডাইহেড্রাল কোণের দ্বিখণ্ডক সমতলগুলি যদি 1ম বিন্দুতে ছেদ করে (একটি প্রয়োজনীয় এবং যথেষ্ট শর্ত) তাহলে একটি গোলক একটি পিরামিডে খোদাই করা যেতে পারে। এই বিন্দুটি গোলকের কেন্দ্রে পরিণত হবে।

সবচেয়ে সহজ পিরামিড।

কোণের সংখ্যার উপর ভিত্তি করে, পিরামিডের ভিত্তিটি ত্রিভুজাকার, চতুর্ভুজাকার ইত্যাদিতে বিভক্ত।

পিরামিড থাকবে ত্রিভুজাকার, চতুর্ভুজাকার, এবং তাই, যখন পিরামিডের ভিত্তি একটি ত্রিভুজ, একটি চতুর্ভুজ, এবং তাই। একটি ত্রিভুজাকার পিরামিড একটি টেট্রাহেড্রন - একটি টেট্রাহেড্রন। চতুর্ভুজ - পঞ্চভুজ এবং তাই।

সংজ্ঞা

পিরামিডএকটি বহুভুজ \(A_1A_2...A_n\) এবং \(n\) একটি সাধারণ শীর্ষবিন্দু \(P\) (বহুভুজের সমতলে শুয়ে নেই) এবং এর বিপরীত দিকগুলির সাথে মিলিত ত্রিভুজ দ্বারা গঠিত একটি পলিহেড্রন বহুভুজের বাহু।
পদবী: \(PA_1A_2...A_n\)।
উদাহরণ: পঞ্চভুজ পিরামিড \(PA_1A_2A_3A_4A_5\)।

ত্রিভুজ \(PA_1A_2, \PA_2A_3\), ইত্যাদি। ডাকল পাশের মুখপিরামিড, সেগমেন্ট \(PA_1, PA_2\), ইত্যাদি - পার্শ্বীয় পাঁজর, বহুভুজ \(A_1A_2A_3A_4A_5\) – ভিত্তি, পয়েন্ট \(P\) - শীর্ষ.

উচ্চতাপিরামিড হল একটি লম্ব যা পিরামিডের শীর্ষ থেকে বেসের সমতলে নেমে আসে।

একটি পিরামিড যার ভিত্তি একটি ত্রিভুজ আছে টেট্রাহেড্রন.

পিরামিড বলা হয় সঠিক, যদি এর ভিত্তি একটি নিয়মিত বহুভুজ হয় এবং নিম্নলিখিত শর্তগুলির মধ্যে একটি পূরণ করা হয়:

\((a)\) পিরামিডের পার্শ্বীয় প্রান্তগুলি সমান;

\((b)\) পিরামিডের উচ্চতা বেসের কাছাকাছি ঘেরা বৃত্তের কেন্দ্রের মধ্য দিয়ে যায়;

\((c)\) পাশের পাঁজরগুলি একই কোণে বেসের সমতলের দিকে ঝুঁকে আছে।

\((d)\) পাশের মুখগুলি একই কোণে বেসের সমতলে ঝুঁকে আছে।

নিয়মিত টেট্রাহেড্রনএকটি ত্রিভুজাকার পিরামিড, যার সমস্ত মুখই সমান সমবাহু ত্রিভুজ।

উপপাদ্য

শর্তগুলি \((a), (b), (c), (d)\) সমতুল্য।

প্রমাণ

আসুন পিরামিডের উচ্চতা খুঁজে বের করি \(PH\)। ধরুন \(\আলফা\) পিরামিডের ভিত্তির সমতল।

1) আসুন প্রমাণ করি যে \((a)\) থেকে এটি \((b)\) অনুসরণ করে। চলুন \(PA_1=PA_2=PA_3=...=PA_n\)।

কারণ \(PH\perp \alpha\), তারপর \(PH\) এই সমতলে থাকা যেকোনো রেখার লম্ব, যার মানে ত্রিভুজগুলি সমকোণ। এর মানে হল এই ত্রিভুজগুলি সাধারণ লেগ \(PH\) এবং কর্ণিক \(PA_1=PA_2=PA_3=...=PA_n\) সমান। এর মানে \(A_1H=A_2H=...=A_nH\)। এর মানে হল যে বিন্দুগুলি \(A_1, A_2, ..., A_n\) বিন্দু \(H\) থেকে একই দূরত্বে রয়েছে, তাই, তারা ব্যাসার্ধের সাথে একই বৃত্তে অবস্থান করে \(A_1H\)। এই বৃত্তটি, সংজ্ঞা অনুসারে, বহুভুজ \(A_1A_2...A_n\) সম্পর্কে সীমাবদ্ধ।

2) আসুন প্রমাণ করি যে \((b)\) বোঝায় \((c)\)।

\(PA_1H, PA_2H, PA_3H,..., PA_nH\)আয়তক্ষেত্রাকার এবং দুই পায়ে সমান। এর মানে হল যে তাদের কোণগুলিও সমান, তাই, \(\কোণ PA_1H=\কোণ PA_2H=...=\কোণ PA_nH\).

3) আসুন প্রমাণ করি যে \((c)\) বোঝায় \((a)\)।

প্রথম বিন্দুর অনুরূপ, ত্রিভুজ \(PA_1H, PA_2H, PA_3H,..., PA_nH\)আয়তক্ষেত্রাকার এবং পা বরাবর এবং ধারালো কোণ. এর মানে হল যে তাদের কর্ণগুলিও সমান, অর্থাৎ, \(PA_1=PA_2=PA_3=...=PA_n\)।

4) আসুন প্রমাণ করি যে \((b)\) বোঝায় \((d)\)।

কারণ একটি নিয়মিত বহুভুজে বৃত্তাকার এবং খোদাই করা বৃত্তের কেন্দ্রগুলি মিলে যায় (সাধারণত বলতে গেলে, এই বিন্দুটিকে একটি নিয়মিত বহুভুজের কেন্দ্র বলা হয়), তারপর \(H\) হল খোদাই করা বৃত্তের কেন্দ্র। আসুন \(H\) বিন্দু থেকে ভিত্তির পাশে লম্ব আঁকুন: \(HK_1, HK_2\), ইত্যাদি। এগুলি খোদাই করা বৃত্তের ব্যাসার্ধ (সংজ্ঞা অনুসারে)। তারপর, TTP অনুসারে (\(PH\) হল সমতলের একটি লম্ব, \(HK_1, HK_2\), ইত্যাদি হল বাহুতে লম্ব প্রক্ষেপণ) বাঁক \(PK_1, PK_2\), ইত্যাদি। বাহুর লম্ব \(A_1A_2, A_2A_3\), ইত্যাদি। যথাক্রমে সুতরাং, সংজ্ঞা দ্বারা \(\কোণ PK_1H, \কোণ PK_2H\)পাশের মুখ এবং ভিত্তির মধ্যে কোণগুলির সমান। কারণ ত্রিভুজ \(PK_1H, PK_2H, ...\) সমান (দুই বাহুর আয়তাকার হিসাবে), তারপর কোণগুলি \(\কোণ PK_1H, \কোণ PK_2H, ...\)সমান.

5) আসুন প্রমাণ করি যে \((d)\) বোঝায় \((b)\)।

চতুর্থ বিন্দুর মতো, ত্রিভুজগুলি \(PK_1H, PK_2H, ...\) সমান (লেগ এবং তীব্র কোণ বরাবর আয়তক্ষেত্রাকার হিসাবে), যার অর্থ হল অংশগুলি \(HK_1=HK_2=...=HK_n\) সমান. এর মানে, সংজ্ঞা অনুসারে, \(H\) হল বেসে খোদাই করা একটি বৃত্তের কেন্দ্র। কিন্তু যেহেতু নিয়মিত বহুভুজের জন্য, খোদাই করা এবং বৃত্তাকার বৃত্তের কেন্দ্রগুলি একত্রিত হয়, তারপর \(H\) হল পরিধিকৃত বৃত্তের কেন্দ্র। Chtd.

পরিণতি

একটি নিয়মিত পিরামিডের পার্শ্বীয় মুখগুলি সমান সমদ্বিবাহু ত্রিভুজ।

সংজ্ঞা

তার শীর্ষবিন্দু থেকে আঁকা একটি নিয়মিত পিরামিডের পার্শ্বীয় মুখের উচ্চতা বলা হয় apothem.
একটি নিয়মিত পিরামিডের সমস্ত পার্শ্বীয় মুখের অ্যাপোথেমগুলি একে অপরের সমান এবং মধ্যমা এবং দ্বিখণ্ডকও।

গুরুত্বপূর্ণ নোট

1. একটি নিয়মিত ত্রিভুজাকার পিরামিডের উচ্চতা বেসের উচ্চতা (বা দ্বিখণ্ডক, বা মধ্যক) এর ছেদ বিন্দুতে পড়ে (বেসটি একটি নিয়মিত ত্রিভুজ)।

2. একটি নিয়মিত চতুর্ভুজাকার পিরামিডের উচ্চতা ভিত্তির কর্ণগুলির ছেদ বিন্দুতে পড়ে (বেসটি একটি বর্গক্ষেত্র)।

3. একটি নিয়মিত ষড়ভুজ পিরামিডের উচ্চতা বেসের কর্ণগুলির ছেদ বিন্দুতে পড়ে (বেসটি একটি নিয়মিত ষড়ভুজ)।

4. পিরামিডের উচ্চতা বেসে থাকা যেকোনো সরল রেখার সাথে লম্ব।

সংজ্ঞা

পিরামিড বলা হয় আয়তক্ষেত্রাকার, যদি এর পাশের প্রান্তগুলির একটি বেসের সমতলে লম্ব হয়।

গুরুত্বপূর্ণ নোট

1. উ আয়তক্ষেত্রাকার পিরামিডপিরামিডের উচ্চতা বেসের দিকে লম্ব প্রান্ত। অর্থাৎ, \(SR\) হল উচ্চতা।

2. কারণ \(SR\) বেস থেকে যেকোনো রেখার লম্ব, তারপর \(\ত্রিভুজ এসআরএম, \ত্রিভুজ এসআরপি\)- সমকোণী ত্রিভুজ।

3. ত্রিভুজ \(\ত্রিভুজ এসআরএন, \ত্রিভুজ এসআরকে\)- এছাড়াও আয়তক্ষেত্রাকার।
অর্থাৎ, এই প্রান্ত দ্বারা গঠিত যেকোন ত্রিভুজ এবং এই প্রান্তের শীর্ষবিন্দু থেকে যে তির্যক উৎপন্ন হবে তা হবে আয়তক্ষেত্রাকার।

\[(\Large(\text(পিরামিডের আয়তন এবং পৃষ্ঠের ক্ষেত্রফল)))\]

উপপাদ্য

পিরামিডের আয়তন বেসের ক্ষেত্রফলের এক তৃতীয়াংশ এবং পিরামিডের উচ্চতার সমান: \

পরিণতি

ধরুন \(a\) বেসের পাশে, \(h\) পিরামিডের উচ্চতা।

1. একটি নিয়মিত ত্রিভুজাকার পিরামিডের আয়তন হল \(V_(\text(right triangle.pir.))=\dfrac(\sqrt3)(12)a^2h\),

2. একটি নিয়মিত চতুর্ভুজাকার পিরামিডের আয়তন \(V_(\text(right.four.pir.))=\dfrac13a^2h\).

3. একটি নিয়মিত ষড়ভুজ পিরামিডের আয়তন \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).

4. একটি নিয়মিত টেট্রাহেড্রনের আয়তন হল \(V_(\text(ডান টেটার।))=\dfrac(\sqrt3)(12)a^3\).

উপপাদ্য

একটি নিয়মিত পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল বেস এবং অ্যাপোথেমের পরিধির অর্ধেক গুণফলের সমান।

\[(\Large(\text(Frustum)))\]

সংজ্ঞা

একটি নির্বিচারে পিরামিড বিবেচনা করুন \(PA_1A_2A_3...A_n\)। আসুন পিরামিডের পাশের প্রান্তে থাকা একটি নির্দিষ্ট বিন্দুর মাধ্যমে পিরামিডের ভিত্তির সমান্তরাল একটি সমতল আঁকি। এই সমতলটি পিরামিডটিকে দুটি পলিহেড্রায় বিভক্ত করবে, যার একটি পিরামিড (\(PB_1B_2...B_n\)), এবং অন্যটিকে বলা হয় কাটা পিরামিড(\(A_1A_2...A_nB_1B_2...B_n\))।

কাটা পিরামিডের দুটি বেস আছে - বহুভুজ \(A_1A_2...A_n\) এবং \(B_1B_2...B_n\) যা একে অপরের মতো।

একটি ছেঁটে যাওয়া পিরামিডের উচ্চতা হল একটি লম্ব যা উপরের ভিত্তির কিছু বিন্দু থেকে নীচের ভিত্তির সমতলে আঁকা।

গুরুত্বপূর্ণ নোট

1. কাটা পিরামিডের সমস্ত পার্শ্বীয় মুখগুলি ট্র্যাপিজয়েড।

2. একটি নিয়মিত কাটা পিরামিডের ঘাঁটিগুলির কেন্দ্রগুলির সাথে সংযোগকারী অংশটি (অর্থাৎ, একটি নিয়মিত পিরামিডের ক্রস-সেকশন দ্বারা প্রাপ্ত একটি পিরামিড) উচ্চতা।

পিরামিড ধারণা

সংজ্ঞা 1

জ্যামিতিক চিত্র, একটি বহুভুজ দ্বারা গঠিত এবং একটি বিন্দু যা এই বহুভুজের সমতলে থাকে না, বহুভুজের সমস্ত শীর্ষবিন্দুর সাথে সংযুক্ত থাকে তাকে পিরামিড বলা হয় (চিত্র 1)।

যে বহুভুজ থেকে পিরামিড তৈরি করা হয় তাকে পিরামিডের ভিত্তি বলা হয়; ফলস্বরূপ ত্রিভুজগুলি, যখন একটি বিন্দুর সাথে সংযুক্ত হয়, তখন পিরামিডের পার্শ্বমুখ হয়, ত্রিভুজের বাহুগুলি পিরামিডের বাহু এবং বিন্দুটি সাধারণ সমস্ত ত্রিভুজের কাছে পিরামিডের শীর্ষ।

পিরামিডের প্রকারভেদ

পিরামিডের গোড়ায় কোণের সংখ্যার উপর নির্ভর করে একে ত্রিভুজাকার, চতুর্ভুজাকার ইত্যাদি বলা যেতে পারে (চিত্র 2)।

চিত্র ২.

অন্য ধরনের পিরামিড হল নিয়মিত পিরামিড।

আসুন আমরা একটি নিয়মিত পিরামিডের সম্পত্তির পরিচয় করি এবং প্রমাণ করি।

উপপাদ্য ঘ

একটি নিয়মিত পিরামিডের সমস্ত পার্শ্বীয় মুখগুলি সমদ্বিবাহু ত্রিভুজ যা একে অপরের সমান।

প্রমাণ।

$h=SO$ উচ্চতার $S$ শীর্ষবিন্দু সহ একটি নিয়মিত $n-$গোনাল পিরামিড বিবেচনা করুন। বেসের চারপাশে একটি বৃত্ত আঁকুন (চিত্র 4)।

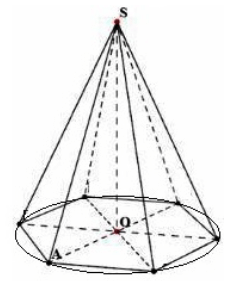
চিত্র 4।

ত্রিভুজ $SOA$ বিবেচনা করুন। পাইথাগোরিয়ান উপপাদ্য অনুসারে, আমরা পাই

স্পষ্টতই, যে কোনও পার্শ্ব প্রান্তকে এইভাবে সংজ্ঞায়িত করা হবে। ফলস্বরূপ, সমস্ত পাশের প্রান্তগুলি একে অপরের সমান, অর্থাৎ, সমস্ত পাশের মুখগুলি সমদ্বিবাহু ত্রিভুজ। আসুন আমরা প্রমাণ করি যে তারা একে অপরের সমান। যেহেতু ভিত্তিটি একটি নিয়মিত বহুভুজ, তাই সমস্ত পাশের মুখগুলির ভিত্তিগুলি একে অপরের সমান। ফলস্বরূপ, ত্রিভুজগুলির সমতার III মানদণ্ড অনুসারে সমস্ত পার্শ্বীয় মুখগুলি সমান।

উপপাদ্য প্রমাণিত হয়েছে।

আসুন এখন নিয়মিত পিরামিডের ধারণার সাথে সম্পর্কিত নিম্নলিখিত সংজ্ঞাটি চালু করি।

সংজ্ঞা 3

একটি নিয়মিত পিরামিডের apothem হল এর পাশের মুখের উচ্চতা।

স্পষ্টতই, থিওরেম ওয়ান দ্বারা, সমস্ত অ্যাপোথেম একে অপরের সমান।

উপপাদ্য 2

একটি নিয়মিত পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল বেস এবং অ্যাপোথেমের আধা-ঘেরের গুণফল হিসাবে নির্ধারিত হয়।

প্রমাণ।

আসুন আমরা $n-$গোনাল পিরামিডের ভিত্তির দিকটিকে $a$ দ্বারা এবং apothemকে $d$ দ্বারা নির্দেশ করি। অতএব, পাশের মুখের ক্ষেত্রফল সমান

যেহেতু, উপপাদ্য 1 অনুযায়ী, সব পক্ষই সমান, তাহলে

উপপাদ্য প্রমাণিত হয়েছে।

আরেকটি ধরনের পিরামিড হল একটি ছোট পিরামিড।

সংজ্ঞা 4

যদি তার ভিত্তির সমান্তরাল একটি সমতল একটি সাধারণ পিরামিডের মাধ্যমে আঁকা হয়, তাহলে এই সমতল এবং ভিত্তিটির সমতলের মধ্যে যে চিত্রটি তৈরি হয় তাকে একটি ছোট পিরামিড (চিত্র 5) বলা হয়।

চিত্র 5. কাটা পিরামিড

কাটা পিরামিডের পার্শ্বীয় মুখগুলি হল ট্র্যাপিজয়েড।

উপপাদ্য 3

একটি নিয়মিত কাটা পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফল বেস এবং অ্যাপোথেমের আধা-ঘেরের যোগফল হিসাবে নির্ধারিত হয়।

প্রমাণ।

আসুন আমরা $n-$গোনাল পিরামিডের ঘাঁটির দিকগুলিকে যথাক্রমে $a\ এবং\b$ দ্বারা এবং apothemকে $d$ দ্বারা নির্দেশ করি। অতএব, পাশের মুখের ক্ষেত্রফল সমান

যেহেতু সব পক্ষই সমান তাই

উপপাদ্য প্রমাণিত হয়েছে।

নমুনা টাস্ক

উদাহরণ 1

একটি কাটা ত্রিভুজাকার পিরামিডের পার্শ্বীয় পৃষ্ঠের ক্ষেত্রফলটি সন্ধান করুন যদি এটি একটি নিয়মিত পিরামিড থেকে বেস সাইড 4 এবং এপোথেম 5 থেকে প্রাপ্ত হয় তবে পাশের মুখগুলির মধ্যরেখা দিয়ে যাওয়া একটি সমতলকে কেটে দিয়ে।

সমাধান।

সম্পর্কে উপপাদ্য দ্বারা মধ্যরেখাআমরা দেখতে পাই যে ছেঁটে যাওয়া পিরামিডের উপরের ভিত্তিটি $4\cdot \frac(1)(2)=2$ এর সমান, এবং apothemটি $5\cdot \frac(1)(2)=2.5$ এর সমান।

তারপর, উপপাদ্য 3 দ্বারা, আমরা পাই