খুব গুরুত্বপূর্ণ তথ্যফাংশনের আচরণ সম্পর্কে বৃদ্ধি এবং হ্রাসের ব্যবধান প্রদান করে। তাদের খুঁজে বের করা ফাংশন পরীক্ষা এবং গ্রাফ প্লট করার প্রক্রিয়ার অংশ। এছাড়াও, যে চরম বিন্দুতে ক্রমবর্ধমান থেকে হ্রাস বা হ্রাস থেকে বৃদ্ধিতে পরিবর্তন হয় তা দেওয়া হয় বিশেষ মনোযোগএকটি নির্দিষ্ট ব্যবধানে একটি ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মান খুঁজে বের করার সময়।
এই নিবন্ধে আমরা দিতে হবে প্রয়োজনীয় সংজ্ঞা, আমরা একটি ব্যবধান এবং একটি চরমের অস্তিত্বের জন্য পর্যাপ্ত শর্তে ফাংশন বৃদ্ধি এবং হ্রাসের একটি পর্যাপ্ত চিহ্ন তৈরি করি এবং উদাহরণ এবং সমস্যা সমাধানের জন্য এই সম্পূর্ণ তত্ত্বটি প্রয়োগ করি।
পৃষ্ঠা নেভিগেশন.
ক্রমবর্ধমান ফাংশনের সংজ্ঞা।
y=f(x) ফাংশনটি X-এর ব্যবধানে বৃদ্ধি পায় যদি কোনটির জন্য হয় এবং 
অসমতা ধরে রাখে। অন্য কথায়, যুক্তির বৃহত্তর মান এর সাথে মিলে যায় উচ্চ মানফাংশন
একটি হ্রাস ফাংশন সংজ্ঞা.
y=f(x) ফাংশনটি X-এর ব্যবধানে হ্রাস পায় যদি কোনটির জন্য এবং অসমতা ধরে রাখে 
. অন্য কথায়, আর্গুমেন্টের একটি বড় মান ফাংশনের একটি ছোট মানের সাথে মিলে যায়।
দ্রষ্টব্য: যদি ফাংশনটি ক্রমবর্ধমান বা হ্রাস ব্যবধানের (a;b) শেষে সংজ্ঞায়িত এবং অবিচ্ছিন্ন থাকে, অর্থাৎ x=a এবং x=b তে, তাহলে এই বিন্দুগুলি ক্রমবর্ধমান বা হ্রাস ব্যবধানে অন্তর্ভুক্ত করা হয়। এটি ব্যবধান X-এ একটি ক্রমবর্ধমান এবং হ্রাসকারী ফাংশনের সংজ্ঞার বিরোধিতা করে না।
উদাহরণস্বরূপ, প্রধান বৈশিষ্ট্য থেকে প্রাথমিক ফাংশনআমরা জানি যে y=sinx সংজ্ঞায়িত এবং যুক্তির সমস্ত বাস্তব মানের জন্য অবিচ্ছিন্ন। অতএব, ব্যবধানে সাইন ফাংশন বৃদ্ধি থেকে, আমরা দৃঢ়ভাবে বলতে পারি যে এটি ব্যবধানে বৃদ্ধি পায়।
বিন্দু বলা হয় সর্বোচ্চ পয়েন্টফাংশন y=f(x) যদি অসমতা তার আশেপাশের সমস্ত x এর জন্য সত্য হয়। সর্বাধিক বিন্দুতে ফাংশনের মান বলা হয় ফাংশনের সর্বোচ্চএবং বোঝান।
বিন্দু বলা হয় সর্বনিম্ন পয়েন্টফাংশন y=f(x) যদি অসমতা তার আশেপাশের সমস্ত x এর জন্য সত্য হয়। ন্যূনতম বিন্দুতে ফাংশনের মান বলা হয় ন্যূনতম ফাংশনএবং বোঝান।
একটি বিন্দুর প্রতিবেশীকে ব্যবধান হিসাবে বোঝা যায় 
, যেখানে যথেষ্ট ছোট ধনাত্মক সংখ্যা।
সর্বনিম্ন এবং সর্বোচ্চ পয়েন্ট বলা হয় চরম পয়েন্ট, এবং এক্সট্রিম পয়েন্টগুলির সাথে সম্পর্কিত ফাংশন মানগুলিকে বলা হয় ফাংশনের চরম.
একটি ফাংশনের এক্সট্রিমাকে বৃহত্তম এবং এর সাথে গুলিয়ে ফেলবেন না সর্বনিম্ন মানফাংশন
প্রথম ছবিতে সর্বোচ্চ মানসেগমেন্টের ফাংশন সর্বাধিক বিন্দুতে অর্জিত হয় এবং এটি ফাংশনের সর্বোচ্চ সমান, এবং দ্বিতীয় চিত্রে - ফাংশনের সর্বোচ্চ মান x=b বিন্দুতে অর্জিত হয়, যা সর্বোচ্চ বিন্দু নয়।
একটি ফাংশনের বৃদ্ধি এবং হ্রাসের জন্য পর্যাপ্ত অবস্থার (লক্ষণ) উপর ভিত্তি করে, ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান পাওয়া যায়।
একটি ব্যবধানে ফাংশন বৃদ্ধি এবং হ্রাসের লক্ষণগুলির সূত্রগুলি এখানে রয়েছে:
সুতরাং, একটি ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান নির্ধারণ করতে, এটি প্রয়োজনীয়:
অ্যালগরিদম ব্যাখ্যা করার জন্য ফাংশন বৃদ্ধি এবং হ্রাসের ব্যবধান খুঁজে বের করার একটি উদাহরণ বিবেচনা করা যাক।
উদাহরণ।
ফাংশন বৃদ্ধি ও হ্রাসের ব্যবধান নির্ণয় কর।
সমাধান।
প্রথম ধাপ হল ফাংশনের সংজ্ঞার ডোমেন খুঁজে বের করা। আমাদের উদাহরণে, হর-এ অভিব্যক্তিটি শূন্যে যাওয়া উচিত নয়, তাই,।
চলুন ফাংশনের ডেরিভেটিভ খুঁজে বের করা যাক: 
একটি পর্যাপ্ত মানদণ্ডের উপর ভিত্তি করে একটি ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান নির্ধারণ করতে, আমরা সংজ্ঞার ডোমেনে অসমতার সমাধান করি। ইন্টারভ্যাল পদ্ধতির একটি সাধারণীকরণ ব্যবহার করা যাক। লবটির একমাত্র আসল মূল হল x = 2, এবং হরটি x=0 এ শূন্যে যায়। এই পয়েন্টগুলি সংজ্ঞার ডোমেনকে বিরতিতে ভাগ করে যেখানে ফাংশনের ডেরিভেটিভ তার চিহ্ন ধরে রাখে। সংখ্যা রেখায় এই বিন্দুগুলো চিহ্নিত করা যাক। আমরা প্রচলিতভাবে প্লাস এবং বিয়োগ দ্বারা বোঝাই যে বিরতিতে ডেরিভেটিভ ধনাত্মক বা ঋণাত্মক। নীচের তীরগুলি পরিকল্পিতভাবে সংশ্লিষ্ট ব্যবধানে ফাংশনের বৃদ্ধি বা হ্রাস দেখায়। 
এইভাবে, 
এবং 
.
বিন্দুতে x=2 ফাংশন সংজ্ঞায়িত এবং অবিচ্ছিন্ন, তাই এটি ক্রমবর্ধমান এবং হ্রাস উভয় ব্যবধানে যোগ করা উচিত। x=0 বিন্দুতে ফাংশনটি সংজ্ঞায়িত করা হয়নি, তাই আমরা এই বিন্দুটিকে প্রয়োজনীয় ব্যবধানে অন্তর্ভুক্ত করি না।
আমরা এটির সাথে প্রাপ্ত ফলাফলের তুলনা করার জন্য ফাংশনের একটি গ্রাফ উপস্থাপন করি।
উত্তর:
সাথে ফাংশন বৃদ্ধি পায় 
, ব্যবধানে হ্রাস পায় (0;2]।
একটি ফাংশনের ম্যাক্সিমা এবং মিনিমা খুঁজে বের করতে, আপনি এক্সট্রিমামের তিনটি চিহ্নের যেকোনো একটি ব্যবহার করতে পারেন, অবশ্যই, যদি ফাংশনটি তাদের শর্তগুলিকে সন্তুষ্ট করে। সবচেয়ে সাধারণ এবং সুবিধাজনক তাদের মধ্যে প্রথম।
y=f(x) ফাংশনটিকে বিন্দুর -আশেপাশে পার্থক্যযোগ্য এবং বিন্দুতেই অবিচ্ছিন্ন হতে দিন।
অন্য কথায়:
একটি ফাংশনের এক্সট্রিমামের প্রথম চিহ্নের উপর ভিত্তি করে এক্সট্রিম পয়েন্ট খুঁজে বের করার জন্য অ্যালগরিদম।
অনেকগুলি শব্দ আছে, আসুন একটি ফাংশনের এক্সট্রিমামের জন্য প্রথম পর্যাপ্ত শর্ত ব্যবহার করে একটি ফাংশনের এক্সট্রিমাম পয়েন্ট এবং এক্সট্রিমা খোঁজার কয়েকটি উদাহরণ আরও ভালভাবে দেখি।
উদাহরণ।
ফাংশনের চরমপত্র খুঁজুন।
সমাধান।
একটি ফাংশনের ডোমেইন হল x=2 ছাড়া বাস্তব সংখ্যার সম্পূর্ণ সেট।
ডেরিভেটিভ খোঁজা: 
লবের শূন্য বিন্দু x=-1 এবং x=5, হর x=2 এ শূন্যে যায়। সংখ্যা অক্ষের উপর এই বিন্দু চিহ্নিত করুন 
আমরা প্রতিটি ব্যবধানে ডেরিভেটিভের চিহ্ন নির্ধারণ করি; এটি করার জন্য, আমরা প্রতিটি ব্যবধানের যেকোনো পয়েন্টে ডেরিভেটিভের মান গণনা করি, উদাহরণস্বরূপ, x=-2, x=0, x=3 এবং বিন্দুতে x=6।
অতএব, ব্যবধানে ডেরিভেটিভটি ধনাত্মক (চিত্রে আমরা এই ব্যবধানের উপরে একটি প্লাস চিহ্ন রাখি)। একইভাবে 
অতএব, আমরা দ্বিতীয় ব্যবধানের উপরে একটি বিয়োগ, তৃতীয়টির উপরে একটি বিয়োগ এবং চতুর্থটির উপরে একটি প্লাস রাখি।
ফাংশন ক্রমাগত এবং এর ডেরিভেটিভ পরিবর্তন সাইন যেখানে পয়েন্ট নির্বাচন করা অবশেষ। এই চরম পয়েন্ট.
বিন্দুতে x=-1 ফাংশনটি অবিচ্ছিন্ন এবং ডেরিভেটিভ পরিবর্তন চিহ্নটি প্লাস থেকে বিয়োগ পর্যন্ত, তাই, এক্সট্রিমের প্রথম চিহ্ন অনুসারে, x=-1 হল সর্বাধিক বিন্দু, ফাংশনের সর্বাধিক এটির সাথে মিলে যায় 
.
বিন্দুতে x=5 ফাংশনটি অবিচ্ছিন্ন এবং ডেরিভেটিভ পরিবর্তনগুলি বিয়োগ থেকে প্লাস পর্যন্ত চিহ্ন, তাই, x=-1 হল সর্বনিম্ন বিন্দু, ফাংশনের সর্বনিম্ন এটির সাথে মিলে যায় 
.
গ্রাফিক ইলাস্ট্রেশন।
উত্তর:
অনুগ্রহ করে দ্রষ্টব্য: একটি চরমের জন্য প্রথম পর্যাপ্ত মানদণ্ডের জন্য বিন্দুতেই ফাংশনের পার্থক্যের প্রয়োজন হয় না।
উদাহরণ।
ফাংশনের এক্সট্রিমাম পয়েন্ট এবং এক্সট্রিমা খুঁজুন 
.
সমাধান।
একটি ফাংশনের ডোমেইন হল বাস্তব সংখ্যার সম্পূর্ণ সেট। ফাংশন নিজেই লেখা যেতে পারে: 
চলুন ফাংশনের ডেরিভেটিভ খুঁজে বের করা যাক: 
বিন্দুতে x=0 ডেরিভেটিভের অস্তিত্ব নেই, যেহেতু একতরফা সীমার মানগুলি মিলিত হয় না যখন যুক্তিটি শূন্যের দিকে থাকে: 
একই সময়ে, মূল ফাংশনটি x=0 বিন্দুতে অবিচ্ছিন্ন থাকে (ধারাবাহিকতার জন্য ফাংশন অধ্যয়নের বিভাগটি দেখুন): 
আসুন আর্গুমেন্টের মান খুঁজে দেখি যেখানে ডেরিভেটিভ শূন্যে যায়: 
আসুন সংখ্যা রেখায় সমস্ত প্রাপ্ত বিন্দু চিহ্নিত করি এবং প্রতিটি ব্যবধানে ডেরিভেটিভের চিহ্ন নির্ধারণ করি। এটি করার জন্য, আমরা প্রতিটি ব্যবধানের নির্বিচারে বিন্দুতে ডেরিভেটিভের মান গণনা করি, উদাহরণস্বরূপ, এ x=-6, x=-4, x=-1, x=1, x=4, x=6.
এটাই, 
এইভাবে, একটি extremum প্রথম চিহ্ন অনুযায়ী, ন্যূনতম পয়েন্ট হয় 
, সর্বোচ্চ পয়েন্ট হয় 
.
আমরা ফাংশনের সংশ্লিষ্ট মিনিমা গণনা করি 
আমরা ফাংশনের সংশ্লিষ্ট ম্যাক্সিমা গণনা করি 
গ্রাফিক ইলাস্ট্রেশন।
উত্তর:
.
যেমন আপনি দেখতে পাচ্ছেন, একটি ফাংশনের চরমতম এই চিহ্নটির জন্য বিন্দুতে কমপক্ষে দ্বিতীয় ক্রম পর্যন্ত একটি ডেরিভেটিভের অস্তিত্ব প্রয়োজন।
ফাংশন বৃদ্ধি এবং হ্রাস ফাংশন y = চ(এক্স)কে ব্যবধানে বৃদ্ধি বলা হয় [ ক, খ], পয়েন্ট কোনো জোড়া জন্য যদি এক্সএবং এক্স", a ≤ x অসমতা ধারণ করে চ(এক্স) ≤
চ (এক্স"), এবং কঠোরভাবে বৃদ্ধি - যদি অসমতা চ (এক্স) চ(এক্স") হ্রাস এবং কঠোরভাবে হ্রাস ফাংশন একইভাবে সংজ্ঞায়িত করা হয়। উদাহরণস্বরূপ, ফাংশন এ = এক্স 2 (চাল
, ক) সেগমেন্টে কঠোরভাবে বৃদ্ধি পায়, এবং (চাল
, b) এই সেগমেন্টে কঠোরভাবে হ্রাস পায়। ক্রমবর্ধমান ফাংশন মনোনীত করা হয় চ (এক্স), এবং কমছে চ (এক্স)↓ একটি পার্থক্যযোগ্য ফাংশন জন্য চ (এক্স) সেগমেন্টে বাড়ছিল [ ক, খ], এটি প্রয়োজনীয় এবং যথেষ্ট যে এর ডেরিভেটিভ চ"(এক্স) নন-নেতিবাচক ছিল [ ক, খ]. একটি অংশে একটি ফাংশনের বৃদ্ধি এবং হ্রাসের পাশাপাশি, আমরা একটি বিন্দুতে একটি ফাংশনের বৃদ্ধি এবং হ্রাস বিবেচনা করি। ফাংশন এ = চ (এক্স) বিন্দুতে বৃদ্ধি বলা হয় এক্স 0 যদি বিন্দু সমন্বিত একটি ব্যবধান (α, β) থাকে এক্স 0, যে কোন বিন্দু জন্য এক্সথেকে (α, β), x> এক্স 0, অসমতা ধরে রাখে চ (এক্স 0) ≤
চ (এক্স), এবং যেকোনো পয়েন্টের জন্য এক্সথেকে (α, β), x 0, অসমতা ধরে রাখে চ (এক্স) ≤ চ (এক্স 0)। বিন্দুতে একটি ফাংশনের কঠোর বৃদ্ধি একইভাবে সংজ্ঞায়িত করা হয় এক্স 0 যদি চ"(এক্স 0) >
0, তারপর ফাংশন চ(এক্স) বিন্দুতে কঠোরভাবে বৃদ্ধি পায় এক্স 0 যদি চ (এক্স) ব্যবধানের প্রতিটি বিন্দুতে বৃদ্ধি পায় ( ক, খ), তারপর এই ব্যবধানে এটি বৃদ্ধি পায়। এস.বি. স্টেককিন।
বড় সোভিয়েত বিশ্বকোষ. - এম.: সোভিয়েত এনসাইক্লোপিডিয়া. 1969-1978 .
ধারণা গাণিতিক বিশ্লেষণ. ফাংশন f(x) বলা হয় জনসংখ্যার বিভিন্ন বয়সের সংখ্যার অনুপাত যা জনসংখ্যার বয়স কাঠামোর সেগমেন্টে বৃদ্ধি পায়। জন্ম ও মৃত্যুর হার, মানুষের আয়ু নির্ভর করে... বড় বিশ্বকোষীয় অভিধান
গাণিতিক বিশ্লেষণের ধারণা। x1 এবং x2, a≤x1 বিন্দুর যেকোন জোড়ার জন্য যদি একটি ফাংশন f(x) সেগমেন্টে বৃদ্ধি পাচ্ছে বলে বলা হয়... বিশ্বকোষীয় অভিধান
গণিতের ধারণা। বিশ্লেষণ ফাংশন f(x) বলা হয়। সেগমেন্টে [a, b] ক্রমবর্ধমান, যদি x1 এবং x2 পয়েন্টের কোনো জোড়ার জন্য, এবং<или=х1 <х<или=b, выполняется неравенство f(x1)
গণিতের একটি শাখা যা ফাংশনের ডেরিভেটিভ এবং ডিফারেনশিয়াল এবং ফাংশন অধ্যয়নের জন্য তাদের প্রয়োগগুলি অধ্যয়ন করে। ডি এর ডিজাইন এবং। একটি স্বাধীন গাণিতিক শাখায় আই. নিউটন এবং জি. লিবনিজের নামের সাথে যুক্ত রয়েছে (17 এর দ্বিতীয়ার্ধ ... গ্রেট সোভিয়েত এনসাইক্লোপিডিয়া
গণিতের একটি শাখা যেখানে ডেরিভেটিভ এবং ডিফারেনশিয়ালের ধারণা এবং কীভাবে তারা ফাংশন অধ্যয়নের জন্য প্রয়োগ করা হয় তা অধ্যয়ন করা হয়। ডি এর উন্নয়ন এবং অবিচ্ছেদ্য ক্যালকুলাসের বিকাশের সাথে ঘনিষ্ঠভাবে সম্পর্কিত। তাদের বিষয়বস্তুও অবিচ্ছেদ্য। তারা একসাথে ভিত্তি তৈরি করে...... গাণিতিক বিশ্বকোষ
এই শব্দটির অন্যান্য অর্থ রয়েছে, ফাংশন দেখুন। "প্রদর্শন" অনুরোধটি এখানে পুনঃনির্দেশিত হয়েছে; অন্যান্য অর্থও দেখুন... উইকিপিডিয়া
অ্যারিস্টটল এবং পেরিপেটেটিক্স- অ্যারিস্টটলের প্রশ্ন অ্যারিস্টটলের জীবনী অ্যারিস্টটলের জন্ম ৩৮৪/৩৮৩ সালে। বিসি e স্ট্যাগিরাতে, মেসিডোনিয়া সীমান্তে। তার পিতা, নাম নিকোমাকাস, ফিলিপের পিতা ম্যাসেডোনিয়ার রাজা অ্যামিন্টাসের সেবায় একজন চিকিৎসক ছিলেন। তার পরিবারের সাথে, তরুণ অ্যারিস্টটল... ... পশ্চিমা দর্শন তার উত্স থেকে বর্তমান দিন পর্যন্ত
- (QCD), কোয়ার্ক এবং গ্লুনের শক্তিশালী মিথস্ক্রিয়ার কোয়ান্টাম ক্ষেত্র তত্ত্ব, কোয়ান্টামের চিত্রে নির্মিত। ইলেক্ট্রোডায়নামিক্স (QED) "রঙ" গেজ প্রতিসাম্যের উপর ভিত্তি করে। QED এর বিপরীতে, QCD-তে ফার্মিয়নগুলির পরিপূরক বৈশিষ্ট্য রয়েছে। স্বাধীনতার কোয়ান্টাম ডিগ্রী সংখ্যা,… শারীরিক বিশ্বকোষ
আই হার্ট হার্ট (ল্যাটিন কোর, গ্রীক কার্ডিয়া) একটি ফাঁপা ফাইব্রোমাসকুলার অঙ্গ যা একটি পাম্প হিসাবে কাজ করে, সংবহনতন্ত্রে রক্ত চলাচল নিশ্চিত করে। অ্যানাটমি হৃৎপিণ্ড পেরিকার্ডিয়ামের পূর্ববর্তী মিডিয়াস্টিনামে (মিডিয়াস্টিনাম) অবস্থিত... ... মেডিকেল এনসাইক্লোপিডিয়া
একটি উদ্ভিদের জীবন, অন্যান্য জীবন্ত প্রাণীর মতো, আন্তঃসম্পর্কিত প্রক্রিয়াগুলির একটি জটিল সেট; তাদের মধ্যে সবচেয়ে উল্লেখযোগ্য, যেমনটি পরিচিত, পরিবেশের সাথে পদার্থের বিনিময়। পরিবেশ হল উৎস যেখান থেকে...... জৈবিক বিশ্বকোষ
"ফাংশন বৃদ্ধি এবং হ্রাস"
পাঠের উদ্দেশ্য:
1. একঘেয়েমি সময়কাল খুঁজে পেতে শিখুন.
2. চিন্তা করার ক্ষমতার বিকাশ যা পরিস্থিতির বিশ্লেষণ নিশ্চিত করে এবং পর্যাপ্ত কর্ম পদ্ধতির বিকাশ (বিশ্লেষণ, সংশ্লেষণ, তুলনা)।
3. বিষয়ের প্রতি আগ্রহ তৈরি করা।
ক্লাস চলাকালীনআজ আমরা ডেরিভেটিভের প্রয়োগ অধ্যয়ন চালিয়ে যাচ্ছি এবং ফাংশন অধ্যয়নের জন্য এর প্রয়োগের প্রশ্নটি বিবেচনা করছি। সামনে কাজ
এখন "Brainstorming" ফাংশনের বৈশিষ্ট্যগুলির কিছু সংজ্ঞা দেওয়া যাক।
1. ফাংশন কাকে বলে?
2. X চলকের নাম কি?
3. Y চলকের নাম কি?
4. একটি ফাংশনের ডোমেইন কি?
5. একটি ফাংশনের মান সেট কি?
6. কোন ফাংশনকে জোড় বলা হয়?
7. কোন ফাংশনকে বিজোড় বলা হয়?
8. একটি জোড় ফাংশনের গ্রাফ সম্পর্কে আপনি কি বলতে পারেন?
9. একটি বিজোড় ফাংশনের গ্রাফ সম্পর্কে আপনি কি বলতে পারেন?
10. কি ফাংশন বৃদ্ধি বলা হয়?
11. কোন ফাংশনকে হ্রাস বলা হয়?
12. কোন ফাংশনকে পর্যায়ক্রমিক বলা হয়?
গণিত হল গাণিতিক মডেলের অধ্যয়ন। সবচেয়ে গুরুত্বপূর্ণ গাণিতিক মডেলগুলির মধ্যে একটি হল একটি ফাংশন। ফাংশন বর্ণনা করার বিভিন্ন উপায় আছে। কোনটি সবচেয়ে সুস্পষ্ট?
- গ্রাফিক।
- কিভাবে একটি গ্রাফ তৈরি করতে হয়?
- বিস্তারিতভাবে.
এই পদ্ধতিটি উপযুক্ত যদি আপনি আগে থেকেই জানেন যে গ্রাফটি প্রায় কেমন দেখাচ্ছে। উদাহরণস্বরূপ, একটি গ্রাফ কি দ্বিঘাত ফাংশন, রৈখিক ফাংশন, বিপরীত সমানুপাতিকতা, ফাংশন y = sinx? (সংশ্লিষ্ট সূত্রগুলি প্রদর্শিত হয়, শিক্ষার্থীরা রেখাচিত্রগুলির নাম দেয়।)
কিন্তু আপনি যদি একটি ফাংশন বা আরও জটিল একটি গ্রাফ প্লট করতে হবে? আপনি একাধিক পয়েন্ট খুঁজে পেতে পারেন, কিন্তু কিভাবে ফাংশন এই পয়েন্টগুলির মধ্যে আচরণ করে?
বোর্ডে দুটি বিন্দু রাখুন এবং শিক্ষার্থীদের "তাদের মধ্যে" গ্রাফটি দেখতে কেমন হতে পারে তা দেখাতে বলুন:
এর ডেরিভেটিভ আপনাকে একটি ফাংশন কিভাবে আচরণ করে তা বের করতে সাহায্য করে।
আপনার নোটবুক খুলুন, নম্বর লিখুন, মহান কাজ.
পাঠের উদ্দেশ্য: কীভাবে একটি ফাংশনের গ্রাফ তার ডেরিভেটিভের গ্রাফের সাথে সম্পর্কিত তা শিখুন এবং দুটি ধরণের সমস্যা সমাধান করতে শিখুন:
1. ডেরিভেটিভ গ্রাফ ব্যবহার করে, ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধানগুলি, সেইসাথে ফাংশনের চরম বিন্দুগুলি খুঁজুন;
2. ব্যবধানে ডেরিভেটিভ লক্ষণগুলির স্কিম ব্যবহার করে, ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধানগুলি, সেইসাথে ফাংশনের চরম বিন্দুগুলি সন্ধান করুন।
অনুরূপ কাজগুলি আমাদের পাঠ্যপুস্তকে নেই, তবে ইউনিফাইড স্টেট পরীক্ষার (অংশ A এবং B) পরীক্ষায় পাওয়া যায়।
আজ পাঠে আমরা প্রক্রিয়াটি অধ্যয়নের দ্বিতীয় পর্যায়ের কাজের একটি ছোট উপাদান দেখব, ফাংশনের একটি বৈশিষ্ট্যের অধ্যয়ন - একঘেয়েতার ব্যবধান নির্ধারণ করা।
এই সমস্যা সমাধানের জন্য, আমাদের আগে আলোচিত কিছু বিষয় স্মরণ করতে হবে।
সুতরাং, আসুন আজকের পাঠের বিষয়টি লিখি: ফাংশন বৃদ্ধি এবং হ্রাসের লক্ষণ।
কার্যকারিতা বৃদ্ধি এবং হ্রাসের লক্ষণ:
যদি প্রদত্ত ফাংশনের ডেরিভেটিভটি ব্যবধানে (a; b) x এর সমস্ত মানের জন্য ধনাত্মক হয়, যেমন f"(x) > 0, তাহলে এই ব্যবধানে ফাংশন বৃদ্ধি পায়।
যদি একটি প্রদত্ত ফাংশনের ডেরিভেটিভটি ব্যবধানে (a; b) x এর সমস্ত মানের জন্য ঋণাত্মক হয়, যেমন f"(x)< 0, то функция в этом интервале убывает
একঘেয়েতার ব্যবধান খোঁজার ক্রম:
ফাংশনের সংজ্ঞার ডোমেন খুঁজুন।
1. ফাংশনের প্রথম ডেরিভেটিভ খুঁজুন।
2. বোর্ডে নিজের জন্য সিদ্ধান্ত নিন
সমালোচনামূলক পয়েন্টগুলি খুঁজুন, ব্যবধানে প্রথম ডেরিভেটিভের চিহ্নটি অনুসন্ধান করুন যেখানে পাওয়া সমালোচনামূলক পয়েন্টগুলি ফাংশনের সংজ্ঞার ডোমেনকে ভাগ করে। ফাংশনের একঘেয়েতার ব্যবধান খুঁজুন:
ক) সংজ্ঞার ক্ষেত্র,
খ) প্রথম ডেরিভেটিভ খুঁজুন:
গ) গুরুত্বপূর্ণ পয়েন্ট খুঁজুন: ; , এবং
3. আসুন ফলাফলের ব্যবধানে ডেরিভেটিভের চিহ্নটি পরীক্ষা করি এবং একটি টেবিলের আকারে সমাধানটি উপস্থাপন করি।
চরম পয়েন্টের দিকে নির্দেশ করুন
ক্রমবর্ধমান এবং হ্রাসের জন্য ফাংশন অধ্যয়নের কয়েকটি উদাহরণ দেখি।
সর্বাধিক অস্তিত্বের জন্য একটি পর্যাপ্ত শর্ত হল "+" থেকে "-" তে ক্রিটিক্যাল পয়েন্টের মধ্য দিয়ে যাওয়ার সময় ডেরিভেটিভের চিহ্ন পরিবর্তন করা এবং সর্বনিম্ন "-" থেকে "+" তে। যদি, ক্রিটিক্যাল পয়েন্টের মধ্য দিয়ে যাওয়ার সময়, ডেরিভেটিভের চিহ্ন পরিবর্তিত না হয়, তাহলে এই বিন্দুতে কোন চরমপন্থা নেই
1. D(f) খুঁজুন।
2. f"(x) খুঁজুন।
3. স্থির বিন্দু খুঁজুন, যেমন বিন্দু যেখানে f"(x) = 0 বা f"(x) বিদ্যমান নেই।
(লবের শূন্যে ডেরিভেটিভটি 0, হরটির শূন্যে ডেরিভেটিভের অস্তিত্ব নেই)
4. স্থানাঙ্ক লাইনে D(f) এবং এই বিন্দুগুলি রাখুন।
5. প্রতিটি ব্যবধানে ডেরিভেটিভের চিহ্নগুলি নির্ধারণ করুন
6. চিহ্ন প্রয়োগ করুন।
7. উত্তর লিখুন।
নতুন উপাদান একীকরণ.
শিক্ষার্থীরা জোড়ায় জোড়ায় কাজ করে এবং তাদের নোটবুকে সমাধানটি লিখে রাখে।
ক) y = x³ - 6 x² + 9 x - 9;
b) y = 3 x² - 5x + 4।
বোর্ডে দুইজন কাজ করছেন।
ক) y = 2 x³ – 3 x² – 36 x + 40
b) y = x4-2 x³
3. পাঠের সারাংশ
বাড়ির কাজ: পরীক্ষা (পার্থক্য)
একটি ফাংশনের প্রকৃতি নির্ধারণ করতে এবং তার আচরণ সম্পর্কে কথা বলতে, বৃদ্ধি এবং হ্রাসের ব্যবধান খুঁজে বের করা প্রয়োজন। এই প্রক্রিয়াটিকে ফাংশন গবেষণা এবং গ্রাফিং বলা হয়। একটি ফাংশনের বৃহত্তম এবং ক্ষুদ্রতম মানগুলি খুঁজে বের করার সময় এক্সট্রিম পয়েন্টটি ব্যবহার করা হয়, যেহেতু সেগুলিতে ফাংশনটি ব্যবধান থেকে বৃদ্ধি বা হ্রাস পায়।
এই নিবন্ধটি সংজ্ঞাগুলি প্রকাশ করে, ব্যবধানে বৃদ্ধি এবং হ্রাসের পর্যাপ্ত চিহ্ন এবং একটি চরমের অস্তিত্বের জন্য একটি শর্ত তৈরি করে। এটি উদাহরণ এবং সমস্যা সমাধানের ক্ষেত্রে প্রযোজ্য। ডিফারেনশিয়াটিং ফাংশন সম্পর্কিত বিভাগটি পুনরাবৃত্তি করা উচিত, কারণ সমাধানটির জন্য ডেরিভেটিভ খুঁজে বের করতে ব্যবহার করতে হবে।
Yandex.RTB R-A-339285-1 সংজ্ঞা 1
যে কোনো x 1 ∈ X এবং x 2 ∈ X, x 2 > x 1 এর জন্য, অসমতা f (x 2) > f (x 1) সন্তুষ্ট হলে y = f (x) ব্যবধান x-এ বৃদ্ধি পাবে। অন্য কথায়, আর্গুমেন্টের একটি বৃহত্তর মান ফাংশনের একটি বৃহত্তর মানের সাথে মিলে যায়।
সংজ্ঞা 2
যে কোনো x 1 ∈ X, x 2 ∈ X, x 2 > x 1, সমতা f (x 2) > f (x 1) এর জন্য y = f (x) ফাংশনটি x এর ব্যবধানে হ্রাস পাচ্ছে বলে মনে করা হয় সত্য বলে বিবেচিত হয়। অন্য কথায়, একটি বড় ফাংশন মান একটি ছোট আর্গুমেন্ট মানের সাথে মিলে যায়। নীচের চিত্রটি বিবেচনা করুন।
মন্তব্য: যখন বৃদ্ধি এবং হ্রাসের ব্যবধানের শেষে ফাংশনটি নির্দিষ্ট এবং অবিচ্ছিন্ন থাকে, অর্থাৎ (a; b), যেখানে x = a, x = b, পয়েন্টগুলি বৃদ্ধি এবং হ্রাসের ব্যবধানে অন্তর্ভুক্ত হয়। এটি সংজ্ঞার বিরোধিতা করে না; এর মানে হল এটি x ব্যবধানে ঘটে।
y = sin x টাইপের প্রাথমিক ফাংশনের প্রধান বৈশিষ্ট্য হল আর্গুমেন্টের বাস্তব মানের জন্য নিশ্চিততা এবং ধারাবাহিকতা। এখান থেকে আমরা পাই যে সাইনটি ব্যবধানে বৃদ্ধি পায় - π 2; π 2, তারপর সেগমেন্টে বৃদ্ধির ফর্ম আছে - π 2; π 2।
সংজ্ঞা 3বিন্দু x 0 বলা হয় সর্বোচ্চ পয়েন্ট y = f (x) ফাংশনের জন্য, যখন x এর সমস্ত মানের জন্য অসমতা f (x 0) ≥ f (x) বৈধ। সর্বাধিক ফাংশনএকটি বিন্দুতে ফাংশনের মান, এবং y m a x দ্বারা চিহ্নিত করা হয়।
x 0 বিন্দুটিকে y = f (x) ফাংশনের সর্বনিম্ন বিন্দু বলা হয়, যখন x এর সমস্ত মানের জন্য অসমতা f (x 0) ≤ f (x) বৈধ। ন্যূনতম ফাংশনএকটি বিন্দুতে ফাংশনের মান, এবং y m i n ফর্মের একটি উপাধি রয়েছে।
বিন্দু x 0 এর প্রতিবেশী বিবেচনা করা হয় চরম বিন্দু,এবং ফাংশনের মান যা এক্সট্রিমাম পয়েন্টের সাথে মিলে যায়। নীচের চিত্রটি বিবেচনা করুন।
ফাংশনের সবচেয়ে বড় এবং ক্ষুদ্রতম মান সহ একটি ফাংশনের এক্সট্রিমা। নীচের চিত্রটি বিবেচনা করুন।
প্রথম চিত্রটি বলে যে সেগমেন্ট থেকে ফাংশনের বৃহত্তম মান খুঁজে বের করা প্রয়োজন [a; খ] এটি সর্বাধিক বিন্দু ব্যবহার করে পাওয়া যায় এবং এটি ফাংশনের সর্বোচ্চ মানের সমান, এবং দ্বিতীয় চিত্রটি x = b এ সর্বাধিক বিন্দু খুঁজে পাওয়ার মতো।
একটি ফাংশনের সর্বোচ্চ এবং মিনিমাম খুঁজে বের করার জন্য, ফাংশনটি এই শর্তগুলিকে সন্তুষ্ট করে এমন ক্ষেত্রে চরম চিহ্ন প্রয়োগ করা প্রয়োজন। প্রথম চিহ্নটিকে সবচেয়ে বেশি ব্যবহৃত বলে মনে করা হয়।
একটি ফাংশন y = f (x) দেওয়া যাক, যা x 0 বিন্দুর একটি ε আশেপাশে পার্থক্যযোগ্য, এবং প্রদত্ত বিন্দু x 0-এ ধারাবাহিকতা রয়েছে। এখান থেকে আমরা সেটা পাই
অন্য কথায়, আমরা সাইন সেট করার জন্য তাদের শর্তগুলি পাই:
একটি ফাংশনের সর্বোচ্চ এবং সর্বনিম্ন পয়েন্ট সঠিকভাবে নির্ধারণ করতে, আপনাকে সেগুলি খুঁজে বের করার জন্য অ্যালগরিদম অনুসরণ করতে হবে:
একটি ফাংশনের এক্সট্রিমা খোঁজার কয়েকটি উদাহরণ সমাধান করে অ্যালগরিদম বিবেচনা করা যাক।
উদাহরণ 1
সর্বাধিক এবং সর্বনিম্ন পয়েন্ট খুঁজুন প্রদত্ত ফাংশন y = 2 (x + 1) 2 x - 2।
সমাধান
এই ফাংশনের সংজ্ঞার ডোমেইন হল x = 2 ছাড়া সমস্ত বাস্তব সংখ্যা। প্রথমে, আসুন ফাংশনের ডেরিভেটিভ খুঁজে বের করি এবং পান:
y " = 2 x + 1 2 x - 2 " = 2 x + 1 2 " (x - 2) - (x + 1) 2 (x - 2) " (x - 2) 2 = = 2 2 (x + 1) (x + 1) " (x - 2) - (x + 1) 2 1 (x - 2) 2 = 2 2 (x + 1) (x - 2) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2
এখান থেকে আমরা দেখতে পাচ্ছি যে ফাংশনের শূন্যগুলি হল x = - 1, x = 5, x = 2, অর্থাৎ প্রতিটি বন্ধনীকে শূন্যের সমান করতে হবে। আসুন এটিকে সংখ্যা অক্ষে চিহ্নিত করি এবং পান:
এখন আমরা প্রতিটি ব্যবধান থেকে ডেরিভেটিভের লক্ষণগুলি নির্ধারণ করি। ব্যবধানে অন্তর্ভুক্ত একটি বিন্দু নির্বাচন করা এবং অভিব্যক্তিতে এটি প্রতিস্থাপন করা প্রয়োজন। উদাহরণস্বরূপ, পয়েন্ট x = - 2, x = 0, x = 3, x = 6।
আমরা যে পেতে
y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0, যার মানে হল ব্যবধান - ∞ ; - 1 এর একটি ধনাত্মক ডেরিভেটিভ আছে। একইভাবে, আমরা দেখতে পাই যে
y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2< 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0
যেহেতু দ্বিতীয় ব্যবধান পরিণত শূন্যের চেয়ে কম, যার মানে সেগমেন্টের ডেরিভেটিভ নেতিবাচক হবে। একটি বিয়োগ সঙ্গে তৃতীয়, একটি প্লাস সঙ্গে চতুর্থ. ধারাবাহিকতা নির্ধারণ করতে, আপনাকে ডেরিভেটিভের চিহ্নের দিকে মনোযোগ দিতে হবে; যদি এটি পরিবর্তিত হয় তবে এটি একটি চরম বিন্দু।
আমরা দেখতে পাই যে x = - 1 বিন্দুতে ফাংশনটি অবিচ্ছিন্ন থাকবে, যার অর্থ হল ডেরিভেটিভ + থেকে - চিহ্ন পরিবর্তন করবে। প্রথম চিহ্ন অনুসারে, আমাদের কাছে আছে যে x = - 1 হল সর্বাধিক বিন্দু, যার মানে আমরা পাই
y m a x = y (- 1) = 2 (x + 1) 2 x - 2 x = - 1 = 2 (- 1 + 1) 2 - 1 - 2 = 0
বিন্দু x = 5 নির্দেশ করে যে ফাংশনটি অবিচ্ছিন্ন, এবং ডেরিভেটিভ চিহ্নটি – থেকে + এ পরিবর্তন করবে। এর মানে হল x = -1 হল সর্বনিম্ন বিন্দু, এবং এর নির্ণয়ের ফর্ম আছে
y m i n = y (5) = 2 (x + 1) 2 x - 2 x = 5 = 2 (5 + 1) 2 5 - 2 = 24
গ্রাফিক ইমেজ
উত্তর: y m a x = y (- 1) = 0, y m i n = y (5) = 24।
এটি এই বিষয়টিতে মনোযোগ দেওয়ার মতো যে একটি চরমের জন্য প্রথম পর্যাপ্ত মানদণ্ডের ব্যবহারের জন্য x 0 বিন্দুতে ফাংশনের পার্থক্যের প্রয়োজন হয় না, এটি গণনাকে সহজ করে।
উদাহরণ 2
y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 ফাংশনের সর্বাধিক এবং সর্বনিম্ন বিন্দুগুলি খুঁজুন।
সমাধান।
একটি ফাংশনের ডোমেইন হল সমস্ত বাস্তব সংখ্যা। এটি ফর্মের সমীকরণের একটি সিস্টেম হিসাবে লেখা যেতে পারে:
1 6 x 3 - 2 x 2 - 22 3 x - 8 , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0
তারপরে আপনাকে ডেরিভেটিভ খুঁজে বের করতে হবে:
y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x< 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x >0 y " = - 1 2 x 2 - 4 x - 22 3 , x< 0 1 2 x 2 - 4 x + 22 3 , x > 0
বিন্দু x = 0 এর কোনো ডেরিভেটিভ নেই, কারণ একতরফা সীমার মান ভিন্ন। আমরা এটি পাই:
lim y "x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 (0 - 0) 2 - 4 (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 (0 + 0) 2 - 4 (0 + 0) + 22 3 = + 22 3
এটি অনুসরণ করে যে ফাংশনটি x = 0 বিন্দুতে অবিচ্ছিন্ন থাকে, তারপর আমরা গণনা করি
lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 (0 - 0) - 8 = - 8 লিম y x → 0 + 0 = লিম x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 0 2 + 22 3 0 - 8 = - 8
যখন ডেরিভেটিভ শূন্য হয়ে যায় তখন আর্গুমেন্টের মান খুঁজে বের করার জন্য গণনা করা প্রয়োজন:
1 2 x 2 - 4 x - 22 3 , x< 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0
1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 1 2 22 3 = 4 3 x 3 = 4 + 4 3 2 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 1 2 = 4 - 2 3 3 > 0
প্রতিটি ব্যবধানের চিহ্ন নির্ধারণ করতে সমস্ত প্রাপ্ত বিন্দু একটি সরল রেখায় চিহ্নিত করা আবশ্যক। অতএব, প্রতিটি ব্যবধানের জন্য নির্বিচারে বিন্দুতে ডেরিভেটিভ গণনা করা প্রয়োজন। উদাহরণস্বরূপ, আমরা x = - 6, x = - 4, x = - 1, x = 1, x = 4, x = 6 মান সহ পয়েন্ট নিতে পারি। আমরা যে পেতে
y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3< 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 >0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6< 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 >0 y "(4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 4 2 - 4 4 + 22 3 = - 2 3< 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0
সরলরেখায় ছবিটি দেখতে কেমন
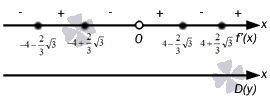
এর মানে হল যে আমরা এই সিদ্ধান্তে উপনীত হয়েছি যে একটি চরমের প্রথম চিহ্নটি অবলম্বন করা প্রয়োজন। আসুন আমরা গণনা করি এবং এটি খুঁজে পাই
x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , তারপর এখান থেকে সর্বোচ্চ পয়েন্টের মান x = - 4 + 2 3 3 , x = 4 - 2 3 3
আসুন ন্যূনতম গণনা করা যাক:
y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3
চলুন ফাংশনের সর্বোচ্চ হিসাব করা যাক। আমরা যে পেতে
y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3
গ্রাফিক ইমেজ
উত্তর:
y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 y 27 x 3 = y 4 - 2 3 3 = 8 27 3
যদি একটি ফাংশন f " (x 0) = 0 দেওয়া হয়, তাহলে f "" (x 0) > 0 হলে, আমরা পাই যে x 0 একটি সর্বনিম্ন বিন্দু যদি f "" (x 0)< 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .
উদাহরণ 3
y = 8 x x + 1 ফাংশনের সর্বোচ্চ এবং মিনিমাম নির্ণয় কর।
সমাধান
প্রথমত, আমরা সংজ্ঞার ডোমেন খুঁজে পাই। আমরা যে পেতে
D(y): x ≥ 0 x ≠ - 1 ⇔ x ≥ 0
ফাংশনটি আলাদা করা প্রয়োজন, যার পরে আমরা পাই
y " = 8 x x + 1 " = 8 x " (x + 1) - x (x + 1) " (x + 1) 2 = = 8 1 2 x (x + 1) - x 1 (x + 1) 2 = 4 x + 1 - 2 x (x + 1) 2 x = 4 - x + 1 (x + 1) 2 x
x = 1 এ, ডেরিভেটিভটি শূন্য হয়ে যায়, যার অর্থ হল বিন্দুটি একটি সম্ভাব্য প্রান্ত। স্পষ্ট করার জন্য, দ্বিতীয় ডেরিভেটিভ খুঁজে বের করতে হবে এবং x = 1 এ মান গণনা করতে হবে। আমরা পেতে:
y "" = 4 - x + 1 (x + 1) 2 x " = 4 (- x + 1) " (x + 1) 2 x - (- x + 1) x + 1 2 x " (x + 1) 4 x = = 4 (- 1) (x + 1) 2 x - (- x + 1) x + 1 2 " x + (x + 1) 2 x " (x + 1) 4 x = = 4 - (x + 1) 2 x - (- x + 1) 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 x = = - (x + 1) 2 x - (- x + 1) x + 1 2 x + x + 1 2 x (x + 1) 4 x = = 2 3 x 2 - 6 x - 1 x + 1 3 x 3 ⇒ y "" (1 ) = 2 3 1 2 - 6 1 - 1 (1 + 1) 3 (1) 3 = 2 · - 4 8 = - 1< 0
এর মানে হল যে একটি এক্সট্রিম্যামের জন্য 2টি যথেষ্ট শর্ত ব্যবহার করে, আমরা পাই যে x = 1 হল সর্বাধিক বিন্দু। অন্যথায়, এন্ট্রিটি y m a x = y (1) = 8 1 1 + 1 = 4 এর মত দেখায়।
গ্রাফিক ইমেজ
উত্তর: y m a x = y (1) = 4 ..
সংজ্ঞা 5y = f (x) ফাংশনটির একটি প্রদত্ত বিন্দু x 0 এর ε আশেপাশে nম ক্রম পর্যন্ত এর ডেরিভেটিভ রয়েছে এবং x 0 বিন্দুতে n + 1ম ক্রম পর্যন্ত এর ডেরিভেটিভ রয়েছে। তারপর f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0।
এটি অনুসরণ করে যে যখন n একটি জোড় সংখ্যা হয়, তখন x 0 একটি প্রবর্তন বিন্দু হিসাবে বিবেচিত হয়, যখন n একটি বিজোড় সংখ্যা হয়, তখন x 0 একটি চরম বিন্দু এবং f (n + 1) (x 0) > 0, তারপর x 0 হল একটি সর্বনিম্ন বিন্দু, f (n + 1) (x 0)< 0 , тогда x 0 является точкой максимума.
উদাহরণ 4
y y = 1 16 (x + 1) 3 (x - 3) 4 ফাংশনের সর্বাধিক এবং সর্বনিম্ন বিন্দুগুলি খুঁজুন।
সমাধান
মূল ফাংশন একটি মূলদ সমগ্র ফাংশন, যার অর্থ হল সংজ্ঞার ডোমেন হল সমস্ত বাস্তব সংখ্যা। এটি ফাংশন পার্থক্য করা প্রয়োজন. আমরা যে পেতে
y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)
এই ডেরিভেটিভ x 1 = - 1, x 2 = 5 7, x 3 = 3 এ শূন্যে যাবে। যে, পয়েন্ট সম্ভাব্য extremum পয়েন্ট হতে পারে. এটি extremum জন্য তৃতীয় যথেষ্ট শর্ত প্রয়োগ করা প্রয়োজন। দ্বিতীয় ডেরিভেটিভ খুঁজে বের করা আপনাকে একটি ফাংশনের সর্বাধিক এবং সর্বনিম্ন উপস্থিতি সঠিকভাবে নির্ধারণ করতে দেয়। দ্বিতীয় ডেরিভেটিভ এর সম্ভাব্য প্রান্তের বিন্দুতে গণনা করা হয়। আমরা যে পেতে
y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401< 0 y "" (3) = 0
এর মানে হল x 2 = 5 7 হল সর্বোচ্চ বিন্দু। 3য় পর্যাপ্ত মানদণ্ড প্রয়োগ করে, আমরা n = 1 এবং f (n + 1) 5 7 এর জন্য পাই< 0 .
x 1 = - 1, x 3 = 3 বিন্দুর প্রকৃতি নির্ধারণ করা প্রয়োজন। এটি করার জন্য, আপনাকে তৃতীয় ডেরিভেটিভটি খুঁজে বের করতে হবে এবং এই পয়েন্টগুলিতে মানগুলি গণনা করতে হবে। আমরা যে পেতে
y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0
এর মানে হল x 1 = - 1 হল ফাংশনের ইনফ্লেকশন পয়েন্ট, যেহেতু n = 2 এবং f (n + 1) (- 1) ≠ 0 এর জন্য। বিন্দু x 3 = 3 তদন্ত করা প্রয়োজন। এটি করার জন্য, আমরা 4 র্থ ডেরিভেটিভ খুঁজে পাই এবং এই সময়ে গণনা সম্পাদন করি:
y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) ( 3) = 96 > 0
উপরে যা সিদ্ধান্ত নেওয়া হয়েছিল তা থেকে আমরা উপসংহারে পৌঁছেছি যে x 3 = 3 হল ফাংশনের সর্বনিম্ন বিন্দু।
গ্রাফিক ইমেজ
উত্তর: x 2 = 5 7 হল সর্বাধিক বিন্দু, x 3 = 3 হল প্রদত্ত ফাংশনের সর্বনিম্ন বিন্দু।
আপনি যদি পাঠ্যটিতে একটি ত্রুটি লক্ষ্য করেন, দয়া করে এটি হাইলাইট করুন এবং Ctrl+Enter টিপুন
গ্রাফ থেকে দ্বিঘাত ফাংশন xy 0 11 বৃদ্ধি এবং হ্রাসের ব্যবধান খুঁজে বের করা xy 0 11 ফাংশনটি ব্যবধানে হ্রাস পাচ্ছে যদি x এর একটি বড় মান y-এর একটি ছোট মানের সাথে মিলে যায়, অর্থাৎ, বাম থেকে ডানে যাওয়ার সময়, গ্রাফটি নিচে চলে যায় ( দেখার জন্য ক্লিক করুন) ব্যবধানে ফাংশনটি বৃদ্ধি পাচ্ছে যদি একটি বড় x মান একটি বৃহত্তর y মানের সাথে মিলে যায়, যেমন, বাম থেকে ডানে যাওয়ার সময়, গ্রাফটি উপরে যায় (দেখতে ক্লিক করুন)
8 y x0 11 গ্রাফ থেকে খুঁজুন এবং দ্বিঘাত ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান লিখুন দয়া করে মনে রাখবেন যে দ্বিঘাত ফাংশনের গ্রাফ দুটি শাখা নিয়ে গঠিত। শাখাগুলি একটি প্যারাবোলার শীর্ষবিন্দু দ্বারা একে অপরের সাথে সংযুক্ত থাকে। বৃদ্ধি এবং হ্রাসের ব্যবধান রেকর্ড করার সময়, সর্বাধিক প্রধান ভূমিকাপ্যারাবোলার শীর্ষবিন্দুর অ্যাবসিসা (x) বাজবে উদাহরণ 1। প্যারাবোলার প্রতিটি শাখা বরাবর গতিবিধি আলাদাভাবে বিবেচনা করুন: বাম শাখা বরাবর, বাম থেকে ডানে যাওয়ার সময়, গ্রাফটি নিচে চলে যায়, যার অর্থ ফাংশন হ্রাস পায়; ডান শাখা বরাবর - গ্রাফ উপরে যায়, যার মানে ফাংশন বাড়ছে। উত্তর: হ্রাস ব্যবধান (- ∞; -1 ]; ক্রমবর্ধমান ব্যবধান [ -1; +∞)
8 y x0 11 গ্রাফ থেকে সন্ধান করুন এবং দ্বিঘাত ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান লিখুন উদাহরণ 2. প্যারাবোলার প্রতিটি শাখা বরাবর গতিবিধি আলাদাভাবে বিবেচনা করুন: বাম শাখা বরাবর, বাম থেকে ডানে যাওয়ার সময়, গ্রাফটি যায় আপ, যার অর্থ ফাংশন বৃদ্ধি পায়; ডান শাখা বরাবর - গ্রাফ নিচে চলে যায়, যার মানে ফাংশনটি হ্রাস পাচ্ছে। উত্তর: বৃদ্ধির ব্যবধান (- ∞; 3]; হ্রাসের ব্যবধান [3; +∞)।
জন্য কাজ স্বাধীন সিদ্ধান্ত(নোটবুকে সম্পূর্ণ) টাস্ক 1 টাস্ক 2 টাস্ক 3 টাস্ক 4 পরিশিষ্ট
ক্রমবর্ধমান ব্যবধান (- ∞; -1 ]; ব্যবধান হ্রাস [ -1; +∞)। উত্তর চেক করুন। গ্রাফ থেকে খুঁজুন এবং দ্বিঘাত ফাংশন বৃদ্ধি এবং হ্রাসের ব্যবধান লিখুন 88 y x0 1 11 অ্যানিমেশনটি দেখুন উত্তরটি নিজেই লিখুন
"কমানোর ব্যবধান (- ∞; 3 ]; ক্রমবর্ধমান ব্যবধান [ 3; +∞)। গ্রাফ থেকে সন্ধান করুন এবং দ্বিঘাত ফাংশন বৃদ্ধি এবং হ্রাসের ব্যবধান লিখুন y x 11 0 8 2 অ্যানিমেশনটি দেখুন উত্তর লিখুন উত্তরটি নিজেই পরীক্ষা করুন
গ্রাফ থেকে খুঁজুন এবং দ্বিঘাত ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান লিখুন 8 y 0 1 1 x3 অ্যানিমেশনটি দেখুন উত্তরটি নিজেই লিখুন হ্রাসের ব্যবধান (- ∞; 0 ]; বৃদ্ধির ব্যবধান [ 0; +∞ ) উত্তর চেক করুন
“গ্রাফ থেকে খুঁজুন এবং দ্বিঘাত ফাংশনের বৃদ্ধি এবং হ্রাসের ব্যবধান লিখুন 8 1 y 01 x4 অ্যানিমেশন দেখুন উত্তরটি নিজেই লিখুন বৃদ্ধির ব্যবধান (- ∞; - 0. 5]; হ্রাসের ব্যবধান [ - 0. 5; + ∞)। উত্তর চেক করুন
পরিশিষ্ট ক্রমবর্ধমান এবং হ্রাসের ব্যবধানের সীমানা বিন্দু হল প্যারাবোলার শীর্ষবিন্দুর অবসিসা। বৃদ্ধি এবং হ্রাসের ব্যবধানের সীমানা বিন্দু সর্বদা একটি বর্গাকার বন্ধনী দিয়ে উত্তরে লেখা হয়, যেহেতু দ্বিঘাত ফাংশনটি অবিচ্ছিন্ন।
