Zde najdete základní informace o pyramidách a souvisejících vzorcích a pojmech. Všechny jsou studovány u učitele matematiky v rámci přípravy na jednotnou státní zkoušku.
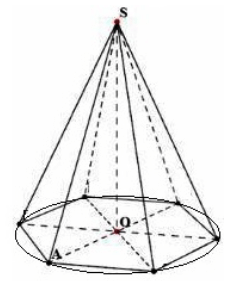
Uvažujme rovinu, mnohoúhelník 
, ležící v něm a bod S, neležící v něm. Spojme S se všemi vrcholy mnohoúhelníku. Výsledný mnohostěn se nazývá pyramida. Segmenty se nazývají boční žebra. 
Mnohoúhelník se nazývá základna a bod S je vrchol pyramidy. Podle čísla n se jehlan nazývá trojúhelníkový (n=3), čtyřboký (n=4), pětiúhelníkový (n=5) a tak dále. Alternativní název pro trojúhelníkovou pyramidu je čtyřstěn. Výška pyramidy je kolmice klesající od jejího vrcholu k rovině základny. 
Pyramida se nazývá pravidelné if pravidelný mnohoúhelník a základna výšky pyramidy (základna kolmice) je jejím středem.
Komentář lektora:
Nezaměňujte pojmy „pravidelná pyramida“ a „pravidelný čtyřstěn“. V pravidelné pyramidě se boční hrany nemusí nutně rovnat hranám základny, ale v pravidelném čtyřstěnu je všech 6 hran stejných. Toto je jeho definice. Je snadné dokázat, že rovnost znamená, že střed P polygonu se shoduje s výškou základny, takže pravidelný čtyřstěn je pravidelný jehlan.
Co je to apotéma?
Apotémou pyramidy je výška její boční strany. Pokud je pyramida pravidelná, pak jsou všechny její apotémy stejné. Opak není pravdou. 
Učitel matematiky o své terminologii: 80 % práce s pyramidami se skládá ze dvou typů trojúhelníků:
1) Obsahuje apotém SK a výšku SP
2) Obsahující boční hranu SA a její průmět PA 
Pro zjednodušení odkazů na tyto trojúhelníky je pro učitele matematiky vhodnější zavolat první z nich apotemální a za druhé žeberní. Tuto terminologii bohužel v žádné z učebnic nenajdete a učitel ji musí zavést jednostranně.
Objemový vzorec pyramidy:
1) 
, kde je plocha základny pyramidy a výška pyramidy
2) , kde je poloměr vepsané koule a je plocha celkového povrchu pyramidy.
3) 
, kde MN je vzdálenost mezi libovolnými dvěma křížícími se hranami a je plocha rovnoběžníku tvořeného středy čtyř zbývajících hran.
Bod P (viz obrázek) se shoduje se středem vepsané kružnice na základně jehlanu, pokud je splněna jedna z následujících podmínek:
1) Všechny apotémy jsou si rovny
2) Všechny boční plochy jsou rovnoměrně nakloněny k základně
3) Všechny apotémy jsou stejně nakloněny k výšce pyramidy
4) Výška jehlanu je rovnoměrně nakloněna ke všem bočním stěnám
Komentář učitele matematiky: Upozorňujeme, že všechny body mají jedno společné obecný majetek: tak či onak, boční plochy jsou zapojeny všude (jejich prvky jsou apotémy). Učitel proto může nabídnout méně přesnou, ale pro učení pohodlnější formulaci: bod P se shoduje se středem vepsané kružnice, základnou pyramidy, pokud existují nějaké stejné informace o jejích bočních stranách. Abychom to dokázali, stačí ukázat, že všechny apotémové trojúhelníky jsou si rovny.
Bod P se shoduje se středem kružnice opsané poblíž základny pyramidy, pokud je splněna jedna ze tří podmínek:
1) Všechny boční hrany jsou stejné
2) Všechna boční žebra jsou rovnoměrně nakloněna k základně
3) Všechna boční žebra jsou stejně nakloněna do výšky
Toto video tutoriál pomůže uživatelům získat představu o tématu pyramidy. Správná pyramida. V této lekci se seznámíme s pojmem pyramida a dáme mu definici. Uvažujme, co je pravidelná pyramida a jaké má vlastnosti. Potom dokážeme větu o boční ploše pravidelného jehlanu.
V této lekci se seznámíme s pojmem pyramida a dáme mu definici.
Zvažte mnohoúhelník A 1 A 2...A n, která leží v rovině α, a bod P, která neleží v rovině α (obr. 1). Pojďme spojit tečky P s vrcholy A 1, A 2, A 3, … A n. Dostaneme n trojúhelníky: A 1 A 2 R, A 2 A 3 R a tak dále.
Definice. Mnohostěn RA 1 A 2 ...A n, tvořeny n-náměstí A 1 A 2...A n A n trojúhelníky RA 1 A 2, RA 2 A 3 …RA n A n-1 se nazývá n-uhelná pyramida. Rýže. 1.
Rýže. 1
Uvažujme o čtyřboké pyramidě PABCD(obr. 2).
R- vrchol pyramidy.
abeceda- základna pyramidy.
RA- boční žebro.
AB- základní žebro.
Od věci R pustíme kolmici RN do základní roviny abeceda. Nakreslená kolmice je výška pyramidy.
Rýže. 2
Celá plocha pyramidy se skládá z boční plochy, tedy plochy všech bočních ploch, a plochy základny:
S plný = S strana + S hlavní
Pyramida se nazývá správná, pokud:
Vysvětlení na příkladu pravidelného čtyřbokého jehlanu
Uvažujme pravidelnou čtyřbokou pyramidu PABCD(obr. 3).
R- vrchol pyramidy. Základna pyramidy abeceda - pravidelný čtyřúhelník, tedy čtverec. Tečka O, průsečík úhlopříček, je středem čtverce. Prostředek, RO je výška pyramidy.
Rýže. 3
Vysvětlení: ve správném n V trojúhelníku se střed vepsané kružnice a střed opsané kružnice shodují. Tento střed se nazývá střed polygonu. Někdy říkají, že vrchol se promítá do středu.
Výška boční stěny pravidelného jehlanu vytaženého z jeho vrcholu se nazývá apotéma a je určeno h a.
1. všechny boční hrany pravidelného jehlanu jsou stejné;
2. Boční plochy jsou stejné rovnoramenné trojúhelníky.
Důkaz těchto vlastností uvedeme na příkladu pravidelného čtyřbokého jehlanu.
Dáno: PABCD- pravidelný čtyřboký jehlan,
abeceda- náměstí,
RO- výška pyramidy.
Dokázat:
1. RA = PB = RS = PD
2.∆ABP = ∆BCP =∆CDP =∆DAP Viz Obr. 4.
Rýže. 4
Důkaz.
RO- výška pyramidy. Tedy rovnou RO kolmo k rovině ABC, a tedy přímé JSC, VO, SO A DĚLAT leží v něm. Takže trojúhelníky ROA, ROV, ROS, ROD- obdélníkový.
Zvažte čtverec abeceda. Z vlastností čtverce vyplývá, že AO = VO = CO = DĚLAT.
Pak pravoúhlé trojúhelníky ROA, ROV, ROS, ROD noha RO- generál a nohy JSC, VO, SO A DĚLAT jsou stejné, což znamená, že tyto trojúhelníky jsou stejné na dvou stranách. Z rovnosti trojúhelníků vyplývá rovnost úseček, RA = PB = RS = PD. Bod 1 se osvědčil.
Segmenty AB A slunce jsou stejné, protože jsou stranami stejného čtverce, RA = PB = RS. Takže trojúhelníky AVR A VSR - rovnoramenné a rovné na třech stranách.
Podobným způsobem zjistíme, že trojúhelníky ABP, VCP, CDP, DAP jsou rovnoramenné a rovné, jak je požadováno prokázat v odstavci 2.
Plocha boční plochy pravidelné pyramidy se rovná polovině součinu obvodu základny a apotému:
Abychom to dokázali, zvolíme pravidelnou trojúhelníkovou pyramidu.
Dáno: RAVS- pravidelný trojúhelníkový jehlan.
AB = BC = AC.
RO- výška.
Dokázat: 
. Viz Obr. 5.
Rýže. 5
Důkaz.
RAVS- pravidelný trojúhelníkový jehlan. To znamená AB= AC = BC. Nechat O- střed trojúhelníku ABC, Pak RO je výška pyramidy. Na základně pyramidy leží rovnostranný trojúhelník ABC. všimněte si, že 
.
Trojúhelníky RAV, RVS, RSA- stejné rovnoramenné trojúhelníky (podle vlastnosti). Trojúhelníková pyramida má tři boční strany: RAV, RVS, RSA. To znamená, že plocha bočního povrchu pyramidy je:
Strana S = 3S RAW
Věta byla prokázána.
Poloměr kruhu vepsaného do základny pravidelné čtyřboké pyramidy je 3 m, výška pyramidy je 4 m. Najděte plochu boční plochy pyramidy.
Dáno: pravidelný čtyřboký jehlan abeceda,
abeceda- náměstí,
r= 3 m,
RO- výška pyramidy,
RO= 4 m.
Nalézt: S strana. Viz Obr. 6.
Rýže. 6
Řešení.
Podle dokázané věty, .
Nejprve najdeme stranu základny AB. Víme, že poloměr kružnice vepsané do paty pravidelného čtyřbokého jehlanu je 3 m.
Potom, m.
Najděte obvod čtverce abeceda se stranou 6 m:
Zvažte trojúhelník BCD. Nechat M- střed strany DC. Protože O- střední BD, Že 
(m).
Trojúhelník DPC- rovnoramenný. M- střední DC. to znamená, RM- medián, a tedy i výška v trojúhelníku DPC. Pak RM- apotéma pyramidy.
RO- výška pyramidy. Pak rovnou RO kolmo k rovině ABC, a tedy přímé OM, ležící v něm. Pojďme najít apotému RM z pravoúhlý trojuhelník ROM.
Nyní můžeme najít boční povrch pyramidy:
Odpovědět: 60 m2.
Poloměr kruhu opsaného kolem základny pravidelné trojúhelníkové pyramidy se rovná m Plocha boční plochy je 18 m2. Najděte délku apotému.
Dáno: ABCP- pravidelná trojúhelníková pyramida,
AB = BC = SA,
R= m,
J strana = 18 m2.
Nalézt: . Viz Obr. 7.
Rýže. 7
Řešení.
V pravoúhlém trojúhelníku ABC Udává se poloměr kružnice opsané. Pojďme najít stranu AB tento trojúhelník pomocí sinusového zákona.
Když známe stranu pravidelného trojúhelníku (m), zjistíme jeho obvod.
Podle věty o boční ploše pravidelné pyramidy, kde h a- apotéma pyramidy. Pak:
Odpovědět: 4 m.
Podívali jsme se tedy, co je pyramida, co je pravidelná pyramida, a dokázali jsme větu o boční ploše pravidelné pyramidy. V další lekci se seznámíme s komolou pyramidou.
Bibliografie
Domácí práce
1. Když mají všechny boční okraje stejnou velikost, pak:
2. Když mají boční plochy úhel sklonu k rovině základny stejné hodnoty, pak:
3. Kouli lze popsat kolem jehlanu, pokud je na základně jehlanu mnohoúhelník, kolem kterého lze popsat kruh (nutná a postačující podmínka). Střed koule bude průsečíkem rovin, které procházejí středy hran jehlanu kolmo k nim. Z této věty vyvozujeme, že kouli lze popsat jak kolem libovolného trojúhelníku, tak kolem libovolné pravidelné pyramidy.
4. Kouli lze vepsat do jehlanu, pokud se roviny os vnitřních dihedrálních úhlů jehlanu protnou v 1. bodě (nutná a postačující podmínka). Tento bod se stane středem koule.
Nejjednodušší pyramida.
Na základě počtu úhlů je základna pyramidy rozdělena na trojúhelníkovou, čtyřhrannou a tak dále.
Bude tam pyramida trojúhelníkový, čtyřúhelníkový, a tak dále, když základna pyramidy je trojúhelník, čtyřúhelník a tak dále. Trojúhelníkový jehlan je čtyřstěn – čtyřstěn. Čtyřúhelníkové - pětiúhelníkové a tak dále.
Definice
Pyramida je mnohostěn složený z mnohoúhelníku \(A_1A_2...A_n\) a \(n\) trojúhelníků se společným vrcholem \(P\) (neležícím v rovině mnohoúhelníku) a protilehlými stranami, které se shodují s strany mnohoúhelníku.
Označení: \(PA_1A_2...A_n\) .
Příklad: pětiboká pyramida \(PA_1A_2A_3A_4A_5\) .
Trojúhelníky \(PA_1A_2, \PA_2A_3\) atd. jsou nazývány boční plochy pyramidy, segmenty \(PA_1, PA_2\) atd. – postranní žebra, mnohoúhelník \(A_1A_2A_3A_4A_5\) – základ, bod \(P\) – horní.
Výška pyramidy jsou kolmice sestupující z vrcholu pyramidy k rovině základny.
Pyramida s trojúhelníkem u základny se nazývá čtyřstěn.
Pyramida se nazývá opravit, pokud je jeho základna pravidelný mnohoúhelník a je splněna jedna z následujících podmínek:
\((a)\) boční okraje pyramidy jsou stejné;
\((b)\) výška jehlanu prochází středem kružnice opsané poblíž základny;
\((c)\) boční žebra jsou skloněna k rovině základny pod stejným úhlem.
\((d)\) boční plochy jsou nakloněny k rovině základny pod stejným úhlem.
Pravidelný čtyřstěn je trojúhelníkový jehlan, jehož všechny strany jsou stejné rovnostranné trojúhelníky.
Teorém
Podmínky \((a), (b), (c), (d)\) jsou ekvivalentní.
Důkaz
Zjistíme výšku pyramidy \(PH\) . Nechť \(\alpha\) je rovina základny pyramidy.
1) Dokažme, že z \((a)\) plyne \((b)\) . Nechť \(PA_1=PA_2=PA_3=...=PA_n\) .
Protože \(PH\perp \alpha\), potom je \(PH\) kolmé k jakékoli přímce ležící v této rovině, což znamená, že trojúhelníky jsou pravoúhlé. To znamená, že tyto trojúhelníky jsou stejné ve společné větvi \(PH\) a přeponě \(PA_1=PA_2=PA_3=...=PA_n\) . To znamená \(A_1H=A_2H=...=A_nH\) . To znamená, že body \(A_1, A_2, ..., A_n\) jsou ve stejné vzdálenosti od bodu \(H\), tedy leží na stejné kružnici o poloměru \(A_1H\) . Tato kružnice je podle definice opsána kolem mnohoúhelníku \(A_1A_2...A_n\) .
2) Dokažme, že \((b)\) implikuje \((c)\) .
\(PA_1H, PA_2H, PA_3H,..., PA_nH\) obdélníkové a stejné na dvou nohách. To znamená, že jejich úhly jsou také stejné, takže \(\úhel PA_1H=\úhel PA_2H=...=\úhel PA_nH\).
3) Dokažme, že \((c)\) implikuje \((a)\) .
Podobně jako v prvním bodě, trojúhelníky \(PA_1H, PA_2H, PA_3H,..., PA_nH\) obdélníkový a podél nohy a ostrý roh. To znamená, že jejich přepony jsou také stejné, tedy \(PA_1=PA_2=PA_3=...=PA_n\) .
4) Dokažme, že \((b)\) implikuje \((d)\) .
Protože v pravidelném mnohoúhelníku se středy opsané a vepsané kružnice shodují (obecně řečeno se tento bod nazývá střed pravidelného mnohoúhelníku), potom je \(H\) středem vepsané kružnice. Nakreslíme kolmice z bodu \(H\) ke stranám podstavy: \(HK_1, HK_2\) atd. Jedná se o poloměry vepsané kružnice (podle definice). Pak podle TTP (\(PH\) je kolmice k rovině, \(HK_1, HK_2\) atd. jsou průměty kolmé ke stranám) nakloněné \(PK_1, PK_2\) atd. kolmo ke stranám \(A_1A_2, A_2A_3\) atd. respektive. Takže podle definice \(\úhel PK_1H, \úhel PK_2H\) rovné úhlům mezi bočními plochami a základnou. Protože trojúhelníky \(PK_1H, PK_2H, ...\) jsou stejné (jako obdélníky na dvou stranách), pak úhly \(\úhel PK_1H, \úhel PK_2H, ...\) jsou rovny.
5) Dokažme, že \((d)\) implikuje \((b)\) .
Podobně jako ve čtvrtém bodě jsou trojúhelníky \(PK_1H, PK_2H, ...\) stejné (jako obdélníkové podél nohy a ostrý úhel), což znamená, že segmenty \(HK_1=HK_2=...=HK_n\) jsou rovnat se. To podle definice znamená, že \(H\) je střed kružnice vepsané do základny. Ale protože U pravidelných mnohoúhelníků se středy kružnice vepsané a kružnice opsané shodují, potom je \(H\) středem kružnice opsané. Chtd.
Následek
Boční stěny pravidelné pyramidy jsou stejné rovnoramenné trojúhelníky.
Definice
Výška boční stěny pravidelného jehlanu vytaženého z jeho vrcholu se nazývá apotéma.
Apotémy všech bočních stěn pravidelné pyramidy jsou si navzájem rovny a jsou také střednicemi a osami.
Důležité poznámky
1. Výška pravidelného trojúhelníkového jehlanu spadá do průsečíku výšek (nebo polos, nebo mediánů) základny (základna je pravidelný trojúhelník).
2. Výška pravidelného čtyřbokého jehlanu spadá do průsečíku úhlopříček podstavy (podstavou je čtverec).
3. Výška pravidelného šestibokého jehlanu spadá do průsečíku úhlopříček podstavy (podstavou je pravidelný šestiúhelník).
4. Výška jehlanu je kolmá k jakékoli přímce ležící u základny.
Definice
Pyramida se nazývá obdélníkový, je-li jedna z jeho bočních hran kolmá k rovině podstavy.
Důležité poznámky
1. U obdélníková pyramida hrana kolmá k základně je výška jehlanu. To znamená, že \(SR\) je výška.
2. Protože \(SR\) je tedy kolmé k jakékoli přímce od základny \(\trojúhelník SRM, \trojúhelník SRP\)– pravoúhlé trojúhelníky.
3. Trojúhelníky \(\triangle SRN, \triangle SRK\)- také obdélníkový.
To znamená, že jakýkoli trojúhelník tvořený touto hranou a úhlopříčkou vycházející z vrcholu této hrany ležící na základně bude obdélníkový.
\[(\Velký(\text(Objem a povrch pyramidy)))\]
Teorém
Objem pyramidy se rovná jedné třetině součinu plochy základny a výšky pyramidy: \
Důsledky
Nechť \(a\) je strana základny, \(h\) je výška pyramidy.
1. Objem pravidelného trojúhelníkového jehlanu je \(V_(\text(pravoúhlý trojúhelník.pir.))=\dfrac(\sqrt3)(12)a^2h\),
2. Objem pravidelného čtyřbokého jehlanu je \(V_(\text(right.four.pir.))=\dfrac13a^2h\).
3. Objem pravidelného šestibokého jehlanu je \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).
4. Objem pravidelného čtyřstěnu je \(V_(\text(pravé tetr.))=\dfrac(\sqrt3)(12)a^3\).
Teorém
Plocha boční plochy pravidelné pyramidy se rovná polovičnímu součinu obvodu základny a apotému.
\[(\Large(\text(Frustum)))\]
Definice
Uvažujme libovolnou pyramidu \(PA_1A_2A_3...A_n\) . Narýsujme rovinu rovnoběžnou se základnou jehlanu přes určitý bod ležící na boční hraně jehlanu. Tato rovina rozdělí pyramidu na dva mnohostěny, z nichž jeden je pyramida (\(PB_1B_2...B_n\)) a druhý se nazývá komolá pyramida(\(A_1A_2...A_nB_1B_2...B_n\) ).
Komolý jehlan má dvě základny - mnohoúhelníky \(A_1A_2...A_n\) a \(B_1B_2...B_n\), které jsou si navzájem podobné.
Výška komolého jehlanu je kolmice vedená z některého bodu horní základny k rovině spodní základny.
Důležité poznámky
1. Všechny boční plochy komolého jehlanu jsou lichoběžníky.
2. Úsečkou spojující středy podstav pravidelného komolého jehlanu (tedy jehlanu získaného příčným řezem pravidelného jehlanu) je výška.
Koncept pyramidy
Definice 1
Geometrický obrazec, tvořený mnohoúhelníkem a bodem neležícím v rovině obsahující tento mnohoúhelník, spojený se všemi vrcholy mnohoúhelníku, se nazývá jehlan (obr. 1).
Mnohoúhelník, ze kterého je pyramida vyrobena, se nazývá základna pyramidy, výsledné trojúhelníky, když jsou spojeny s bodem, jsou bočními plochami jehlanu, stranami trojúhelníků jsou strany jehlanu a společný bod; ke všem trojúhelníkům je vrchol pyramidy.
Podle počtu úhlů na základně pyramidy ji lze nazvat trojúhelníkovou, čtyřúhelníkovou a tak dále (obr. 2).
Obrázek 2
Dalším typem pyramidy je pravidelná pyramida.
Uveďme a dokažme vlastnost pravidelné pyramidy.
Věta 1
Všechny boční stěny pravidelné pyramidy jsou rovnoramenné trojúhelníky, které jsou si navzájem rovné.
Důkaz.
Uvažujme pravidelnou $n-$gonální pyramidu s vrcholem $S$ o výšce $h=SO$. Nakreslete kruh kolem základny (obr. 4).
Obrázek 4.
Uvažujme trojúhelník $SOA$. Podle Pythagorovy věty dostáváme
Je zřejmé, že každá boční hrana bude definována tímto způsobem. V důsledku toho jsou všechny boční hrany navzájem stejné, to znamená, že všechny boční plochy jsou rovnoramenné trojúhelníky. Dokažme, že jsou si navzájem rovni. Protože základna je pravidelný mnohoúhelník, jsou základny všech bočních ploch navzájem stejné. V důsledku toho jsou všechny boční plochy stejné podle III kritéria rovnosti trojúhelníků.
Věta byla prokázána.
Uveďme si nyní následující definici související s pojmem pravidelné pyramidy.
Definice 3
Apotémou pravidelné pyramidy je výška její boční strany.
Je zřejmé, že podle první věty jsou si všechny apotémy navzájem rovny.
Věta 2
Boční plocha pravidelné pyramidy je určena jako součin semi-obvodu základny a apotému.
Důkaz.
Označme stranu podstavy $n-$gonální pyramidy $a$ a apotému $d$. Proto je plocha boční plochy rovna
Protože podle věty 1 jsou všechny strany stejné
Věta byla prokázána.
Dalším typem pyramidy je komolá pyramida.
Definice 4
Je-li obyčejným jehlanem vedena rovina rovnoběžná s jeho podstavou, pak se obrazec vytvořený mezi touto rovinou a rovinou podstavy nazývá komolý jehlan (obr. 5).
Obrázek 5. Komolá pyramida
Boční strany komolého jehlanu jsou lichoběžníky.
Věta 3
Boční plocha pravidelného komolého jehlanu je určena jako součin součtu poloobvodů základen a apotému.
Důkaz.
Označme strany podstav $n-$gonální pyramidy $a\ a\ b$ a apotému $d$. Proto je plocha boční plochy rovna
Protože všechny strany jsou si rovny
Věta byla prokázána.
Příklad 1
Najděte plochu bočního povrchu komolého trojúhelníkového jehlanu, pokud je získán z pravidelného jehlanu se základní stranou 4 a apotémem 5 odříznutím roviny procházející středovou osou bočních ploch.
Řešení.
Podle věty o střední čára zjistíme, že horní základna komolého jehlanu je rovna $4\cdot \frac(1)(2)=2$ a apotéma je rovna $5\cdot \frac(1)(2)=2,5$.
Pak podle věty 3 dostaneme
