Parallel transfer.

TRANSFER ALONG THE Y-AXIS

f(x) => f(x) - b
Let it be required to plot the function y \u003d f (x) - b. It is easy to see that the ordinates of this graph for all values ​​of x on |b| units less than the corresponding ordinates of the graph of functions y = f(x) for b>0 and |b| more units - at b 0 or up at b To plot the function y + b = f(x), plot the function y = f(x) and move the x-axis to |b| units up for b>0 or by |b| units down at b

TRANSFER ALONG THE X-AXIS

f(x) => f(x + a)
Let it be required to plot the function y = f(x + a). Consider a function y = f(x), which at some point x = x1 takes the value y1 = f(x1). Obviously, the function y = f(x + a) will take the same value at the point x2, the coordinate of which is determined from the equality x2 + a = x1, i.e. x2 = x1 - a, and the equality under consideration is valid for the totality of all values ​​from the domain of the function. Therefore, the graph of the function y = f(x + a) can be obtained by parallel displacement of the graph of the function y = f(x) along the x-axis to the left by |a| ones for a > 0 or to the right by |a| units for a To plot the function y = f(x + a), plot the function y = f(x) and move the y-axis to |a| units to the right for a>0 or |a| units to the left for a

Examples:

1.y=f(x+a)

2.y=f(x)+b

Reflection.

GRAPHING OF A FUNCTION OF THE VIEW Y = F(-X)

f(x) => f(-x)
Obviously, the functions y = f(-x) and y = f(x) take equal values ​​at points whose abscissas are equal in absolute value but opposite in sign. In other words, the ordinates of the graph of the function y = f(-x) in the region of positive (negative) values ​​of x will be equal to the ordinates of the graph of the function y = f(x) with negative (positive) x values ​​corresponding in absolute value. Thus, we get the following rule.
To plot the function y = f(-x), you should plot the function y = f(x) and reflect it along the y-axis. The resulting graph is the graph of the function y = f(-x)

GRAPHING OF A FUNCTION OF THE VIEW Y = - F(X)

f(x) => - f(x)
The ordinates of the graph of the function y = - f(x) for all values ​​of the argument are equal in absolute value, but opposite in sign to the ordinates of the graph of the function y = f(x) for the same values ​​of the argument. Thus, we get the following rule.
To plot the function y = - f(x), you should plot the function y = f(x) and reflect it about the x-axis.

Examples:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Deformation.

DEFORMATION OF THE GRAPH ALONG THE Y-AXIS

f(x) => kf(x)
Consider a function of the form y = k f(x), where k > 0. It is easy to see that for equal values ​​of the argument, the ordinates of the graph of this function will be k times greater than the ordinates of the graph of the function y = f(x) for k > 1 or 1/k times less than the ordinates of the graph of the function y = f(x) for k ) or decrease its ordinates by 1/k times for k
k > 1- stretching from the Ox axis
0 - compression to the OX axis

GRAPH DEFORMATION ALONG THE X-AXIS

f(x) => f(kx)
Let it be required to plot the function y = f(kx), where k>0. Consider a function y = f(x), which takes the value y1 = f(x1) at an arbitrary point x = x1. It is obvious that the function y = f(kx) takes the same value at the point x = x2, the coordinate of which is determined by the equality x1 = kx2, and this equality is valid for the totality of all values ​​of x from the domain of the function. Consequently, the graph of the function y = f(kx) is compressed (for k 1) along the abscissa axis relative to the graph of the function y = f(x). Thus, we get the rule.
To plot the function y = f(kx), plot the function y = f(x) and reduce its abscissas by k times for k>1 (compress the graph along the abscissa axis) or increase its abscissas by 1/k times for k
k > 1- compression to the Oy axis
0 - stretching from the OY axis

The work was carried out by Alexander Chichkanov, Dmitry Leonov under the supervision of Tkach T.V., Vyazovov S.M., Ostroverkhova I.V.
©2014

§ 11. Graphs of sine and cosine
Repeat: § 5. Clock, or modern look for trigonometry.
Let's plot the function y = sin x. At the same time, we again
the hours from § 5 are suitable.
If x = 0, then, obviously, y = 0. When x
melts from 0 to π/2, the number sin x increases from 0 to
1 (imagine how the ordinate of the con-
arrows on our signature watches). Plot
graph for x from 0 to π/2 is shown in fig. 11.1.
For small x, our graph is close to a straight line
y = x: remember that for small x
approximate formula sin x ≈ x. You can say
that the line y = x is tangent to the curve with the equation
y = sin x at point (0; 0). Note also that our section of the graph
located below this line: after all, for sharp corners x, measured
in radians, sin x< x.
The closer x is to π/2, the flatter our curve goes. This
occurs because the projection of the end of the arrow onto the y-axis,
oscillating along the segment [−1; 1], moves fastest in the middle
segment and slows down at its edges: we have already discussed this in § 5.

from π to 3π / 2, sin x decreases from 0 to -1, and when x increases from 3π / 2 to 2π, it increases from -1 to 0. So, the graph section for 0 6 x 6 2π is ready (Fig. 11.2 b ). Note, by the way, that the curve in Figure 11.2 a is symmetrical with respect to the vertical straight line with the equation x = π/2. Indeed, the reduction formula sin(π/2 - x) = sin x shows that the points with abscissas x and π - x have the same ordinates on the graph and, therefore, are symmetrical with respect to the straight line x = π/2 (Fig. 11.3 A).

Problem 11.1. Write the equation of a straight line tangent to the graph of the function y = sin x at a point with coordinates (π; 0).

The curve in Fig. 11.2 b is centrally symmetrical with respect to the point with coordinates (π; 0); this follows from another reduction formula: sin(2π - x) = - sin x (Fig. 11.3 b).

After we have a section of the graph of the function y \u003d sin x for 0 6 x 6 2π, the entire graph is already easy to build. Indeed, when the end of the arrow has traveled the path 2π, the arrow has returned to its original position; as you move forward, everything will repeat itself. This means that the graph will consist of the same pieces as in Figure 11.2 b. The final graph of the function y = sin x looks like in Fig. 11.4. At the same time, sections of the graph at x , , [−2π; 0]. . . are obtained from the graph in Figure 11.2 b by shifting along the x-axis by 2π, 4π, −2π,. . . respectively. This is just a restatement of the fact that the function y = sin x has a period of 2π.

Rice. 11.4. y = sinx.

Rice. 11.5. y = cos x.

Now let's plot the function y = cos x. It would be possible to build it in the same way as we built the sine graph. We will, however, choose a different path that will allow us to use the information we already have.

Namely, we use the reduction formula sin(x + π/2) = cos x. This formula can be understood as follows: the function y = cos x takes the same values ​​as the function y = sin x, but π/2 earlier. For example, the function y = sin x takes the value 1 at x = π/2, and the function y = cos x = sin(x + π/2) takes the same value already at x = 0. On the graph, this means the following: for each graph points y \u003d sin x is a graph point y \u003d cos x, whose ordinate is the same, and the abscissa is π / 2 less (Fig. 11.5). Therefore, the graph y = cos x will be obtained if the graph y = sin x is shifted along the x-axis by π/2 to the left. In Figure 11.5, the graph of the function y = cos x is shown as a solid curve.

So, we found out that the cosine graph is obtained by transforming

zation (shift) from the sine graph. The cases when the graph of one function can be obtained by transformation from the graph of another function are interesting in themselves, so let's say a few words about them.

How, for example, will the graph of the function y = 2 sin x look like? It is clear that the ordinates of the points of this graph are obtained from the ordinates of the corresponding points of the graph y \u003d sin x multiplied by 2, so that our graph will be displayed as a solid curve in Fig. 11.6. We can say that the graph y = 2 sin x is obtained from the graph y = sin x by stretching twice along the y-axis.

Rice. 11.6. y = 2 sin x.

Rice. 11.7. y = sin 2x.

Now let's plot the function y = sin 2x. It's easy to understand

Rice. 11.8. y = sin(2x + π/3).

that the function y = sin 2x takes the same values ​​as the function y = sin x, but with twice the values ​​of x. For example, the function y = sin x takes the value 1 at x = π/2, and the function y = sin 2x already at x = π/4; in other words, to get a graph y = sin 2x, it is necessary to halve the abscissas of all points of the graph y = sin x, and leave the ordinates unchanged. What happens is shown in Fig. 11.7. We can say that the graph y \u003d sin 2x (solid line in Fig. 11.7) is obtained from the graph y \u003d sin x by 2 times shrinking to the y-axis.

Let's try to plot the function y = sin(2x + π/3) as well. It is clear that it must be obtained by some kind of transformation from the graph y = sin 2x. At first glance, it may seem that this transformation is a shift to the left by π / 3 along the abscissa axis, by analogy with what is shown in Fig. 11.5. However, if this were the case, then it would turn out, for example, that the function y = sin(2x + π/3) takes on the value 1 at x = π/4 − π/3 = π/12, which is not true (check !). The correct reasoning is: sin(2x + π/3) = sin 2(x + π/6), so the function y = sin(2x+π/3) takes the same values ​​as the function y = sin 2x, but π/6 earlier. So the shift to the left is not by π / 3, but by π / 6 (Fig. 11.8).

Curves that are graphs of functions y \u003d a sin bx, where a 6 \u003d 0, b 6 \u003d 0, are called sinusoids. Note that the “cosine” curve does not need to be introduced: as we have seen, the cosine graph is the same curve as the sine graph, only it is located differently

naya with respect to the coordinate axes.

Problem 11.2. What are the coordinates of the points marked in fig. 11.8 question marks?

Problem 11.3. Take a candle, a thin sheet of paper and a sharp knife. Wind a sheet of paper around the candle in several layers and carefully cut this candle along with the paper obliquely with a knife. Now unfold the paper. You will see that it turned out to be cut along a wavy line. Prove that this wavy line is a sinusoid.

Problem 11.4. Plot the function graphs:

d) y = 3 cos 2x;

a) y = − sinx; b)

c) y = cos(x/2);

g) y = sin(πx). e)

Comment. If you are plotting trigonometric functions on checkered paper, it is convenient to choose slightly different scales along the axes, so that on the x-axis the number π corresponds to an integer number of cells. For example, such a scale is often chosen: along the ordinate axis, a segment of length 1 occupies two cells, along the abscissa axis, a segment of length π occupies 6 cells.

Problem 11.5. Plot the function graphs:

a) y \u003d arcsin x; b) y = arccos x.

Let's see how the solutions of the equations sin x = a and cos x = a already known to us look on the graphs. These solutions are the abscissas of the points of intersection of the horizontal line y = a with the function graph y = sin x (respectively, y = cos x). On fig. 11.9 ,11.10 one can clearly see two series of solutions obtained at −1< a < 1.

The graphs of the sine and cosine show at what intervals these functions increase and at what intervals they decrease. It is clear, for example, that the function y = sin x increases on the intervals [−π/2; π/2],

Function Graph Transformation

In this article, I will introduce you to linear transformations of function graphs and show you how to use these transformations to get a function graph from a function graph.

A linear transformation of a function is a transformation of the function itself and/or its argument to the form , as well as a transformation containing the module of the argument and/or functions.

The following actions cause the greatest difficulties in plotting graphs using linear transformations:

1. The isolation of the base function, in fact, the graph of which we are transforming.
2. Definitions of the order of transformations.

AND It is on these points that we will dwell in more detail.

Let's take a closer look at the function

It is based on a function. Let's call her basic function.

When plotting a function we make transformations of the graph of the base function .

If we were to transform the function in the same order in which its value was found for a certain value of the argument, then

Let's consider what types of linear argument and function transformations exist, and how to perform them.

Argument transformations.

1. f(x) f(x+b)

1. We build a graph of a function

2. We shift the graph of the function along the OX axis by |b| units

• left if b>0
• right if b<0

Let's plot the function

1. We plot the function

2. Shift it 2 units to the right:

2. f(x) f(kx)

1. We build a graph of a function

2. Divide the abscissas of the graph points by k, leave the ordinates of the points unchanged.

Let's plot the function.

1. We plot the function

2. Divide all abscissas of the graph points by 2, leave the ordinates unchanged:

3. f(x) f(-x)

1. We build a graph of a function

2. We display it symmetrically about the OY axis.

Let's plot the function.

1. We plot the function

2. We display it symmetrically about the OY axis:

4. f(x) f(|x|)

1. We plot the function

2. We erase the part of the graph located to the left of the OY axis, the part of the graph located to the right of the OY axis We complete it symmetrically about the OY axis:

The graph of the function looks like this:

Let's plot the function

1. We build a function graph (this is a function graph shifted along the OX axis by 2 units to the left):

2. Part of the graph located to the left of the OY (x<0) стираем:

3. The part of the graph located to the right of the OY axis (x>0) is completed symmetrically with respect to the OY axis:

Important! The two main rules for argument conversion.

1. All argument transformations are performed along the OX axis

2. All transformations of the argument are performed "vice versa" and "in reverse order".

For example, in a function, the sequence of argument transformations is as follows:

1. We take the module from x.

2. Add the number 2 to the modulo x.

But we did the plotting in the reverse order:

First, we performed the transformation 2. - shifted the graph by 2 units to the left (that is, the abscissas of the points were reduced by 2, as if "vice versa")

Then we performed the transformation f(x) f(|x|).

Briefly, the sequence of transformations is written as follows:

Now let's talk about function transformation . Transformations are being made

1. Along the OY axis.

2. In the same sequence in which the actions are performed.

These are the transformations:

1. f(x)f(x)+D

2. Shift it along the OY axis by |D| units

• up if D>0
• down if D<0

Let's plot the function

1. We plot the function

2. Move it along the OY axis by 2 units up:

2. f(x)Af(x)

1. We plot the function y=f(x)

2. We multiply the ordinates of all points of the graph by A, we leave the abscissas unchanged.

Let's plot the function

1. Graph the function

2. We multiply the ordinates of all points of the graph by 2:

3.f(x)-f(x)

1. We plot the function y=f(x)

Let's plot the function.

1. We build a function graph.

2. We display it symmetrically about the OX axis.

4. f(x)|f(x)|

1. We plot the function y=f(x)

2. The part of the graph located above the OX axis is left unchanged, the part of the graph located below the OX axis is displayed symmetrically about this axis.

Let's plot the function

1. We build a function graph. It is obtained by shifting the graph of the function along the OY axis by 2 units down:

2. Now the part of the graph located below the OX axis will be displayed symmetrically with respect to this axis:

And the last transformation, which, strictly speaking, cannot be called a function transformation, since the result of this transformation is no longer a function:

|y|=f(x)

1. We plot the function y=f(x)

2. We erase the part of the graph located below the OX axis, then we complete the part of the graph located above the OX axis symmetrically about this axis.

Let's build a graph of the equation

1. We build a function graph:

2. We erase the part of the graph located below the OX axis:

3. The part of the graph located above the OX axis is completed symmetrically about this axis.

And finally, I suggest you watch the VIDEO LESSON in which I show a step-by-step algorithm for plotting a function graph

The graph of this function looks like this:

It can be seen from the graphs that:

1. Sine and cosine plots fluctuate between -1 and 1
2. The cosine curve has the same shape as the sine curve, but is shifted relative to it by 90 o
3. The sine and cosine curves are continuous and repeat with a period of 360 o , the tangent curve has discontinuities and repeats with a period of 180 o .

On fig. on the left are shown perpendicular axes XX" and YY"; intersecting at the origin O. When working with graphs, measurements to the right and up from O are considered positive, to the left and down from O - negative. Let the OA rotate freely relative to O. When the OA is rotated counterclockwise, the measured angle is considered positive, and when rotated clockwise, it is negative.

Schedule. positive or negative
direction in circular motion.

Let OA rotate counterclockwise in such a way that Θ 1 is any angle in the first quadrant, and construct a perpendicular AB to obtain a right triangle OAB in fig. left. Since all three sides of the triangle are positive, the trigonometric functions sine, cosine, and tangent in the first quadrant will be positive. (Note that the length of OA is always positive because it is the radius of the circle.)
Let OA rotate further in such a way that Θ 2 is any angle in the second quadrant, and construct the AC so that a right triangle OAC is formed. Then sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Let OA rotate further in such a way that Θ 3 is any angle in the third quadrant, and construct AD so that a right triangle OAD is formed. Then sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .

Schedule. Building angles in
various quadrants.

Let OA rotate further in such a way that Θ 4 is any angle in the fourth quadrant, and construct AE so that a right triangle OAE is formed. Then sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.

In the first quadrant, all trigonometric functions have positive values, in the second, only the sine is positive, in the third, only the tangent, in the fourth, only the cosine, which is shown in Fig. left.

Knowledge of angles of arbitrary magnitude is necessary when finding, for example, all angles between 0 o and 360 o whose sine is, say, 0.3261. If you enter 0.3261 into the calculator and press the sin -1 button, we get the answer 19.03 o. However, there is a second angle between 0 o and 360 o that the calculator will not show. The sine is also positive in the second quadrant. The other angle is shown in Fig. below as angle Θ, where Θ=180 o - 19.03 o = 160.97 o . Thus, 19.03 o and 160.97 o are angles in the range from 0 o to 360 o whose sine is 0.3261.

Be careful! The calculator gives only one of these values. The second value should be determined according to the theory of angles of arbitrary magnitude.

Example 1

Find all angles between 0 o and 360 o whose sine is -0.7071

Solution:
Angles whose sine is -0.7071 o are in the third and fourth quadrants because the sine is negative in those quadrants (see figure on the left).

Schedule. Finding all angles by
given sine value (example)

From the following figure Θ = arcsin 0.7071 = 45 o . Two angles in the range from 0 o to 360 o whose sine is -0.7071 are 180 o +45 o \u003d 225 o and 360 o - 45 o \u003d 315 o.

Note. The calculator gives only one answer.
Schedule. Finding all angles by
given sine value (example)

Example 2

Find all angles between 0 o and 360 o whose tangent is 1.327.

Solution:
The tangent is positive in the first and third quadrants - fig. left.
Schedule. Finding all angles by

From the figure below Θ = arctan1,327= 53 o .
Two angles in the range from 0 o to 360 o whose tangent is 1.327 are 53 o and 180 o + 53 o , i.e. 233o.
Schedule. Finding all angles by
given tangent value (example)

Let OR in Fig. on the left is a vector of unit length, freely rotating counterclockwise around O. One revolution produces the circle shown in fig. and divided by sectors of 15 o . Each radius has a horizontal and a vertical component. For example, for 30 o the vertical component is TS and the horizontal component is OS.

From the definition of trigonometric functions
sin30 o =TS/TO=TS/1, i.e. TS=sin30o And cos30 o =OS/TO=OS/1, i.e. OS=cos30o

The vertical component TS can be plotted as T"S", which is equal to the value corresponding to the 30° angle in the y versus x angle plot. If all vertical components, like TS, are transferred to the graph, then a sinusoid will be obtained, shown in Fig. higher.

If all the horizontal components, like OS, are projected onto a plot of y vs. x, you get a cosine wave. These projections are easy to visualize by redrawing a circle with radius OR and angles originating from vertical, as shown in the figure on the left.
From fig. on the left you can see that the sinusoid has the same shape as the cosine wave, but shifted by 90 o .

Periodic functions and period
Each of the function graphs shown in the four Figs. above, is repeated as angle A increases, so they are called periodic functions.
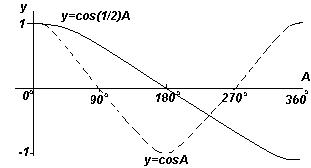
The functions y=sinA and y=cosA are repeated every 360 o (or 2π radians), so 360 o is called period these functions. The functions y=sin2A and y=cos2A repeat every 180 o (or π radians), so 180 o is the period for these functions.
In general, if y=sinpA and y=cospA (where p is a constant), then the period of the function is 360 o /p (or 2π/p radians). Therefore, if y=sin3A, then the period of this function is 360 o /3= 120 o , if y=cos4A, then the period of this function is 360 o /4= 90 o .

Amplitude
Amplitude called the maximum value of the sinusoid. Each of the graphs 1-4 has an amplitude of +1 (i.e. they fluctuate between +1 and -1). However, if y=4sinA, each of the sinA values ​​is multiplied by 4, so the maximum amplitude value is 4. Similarly, for y=5cos2A, the amplitude is 5 and the period is 360 o /2= 180 o .

Example 3
Build y=3sin2A in the range from A= 0 o to A=360 o .

Solution:
Amplitude =3, period = 360 o /2 =180 o .

Example 4
Plot y=4cos2x in the range from x=0 o to x=360 o

Solution:
Amplitude = 4. period = 360 o /2 =180 o .

Lag and lead angles
The sine and cosine curves do not always start at 0 o . To take this circumstance into account, the periodic function is represented as y=sin(A± α), where α is the phase shift with respect to y=sinA and y=cosA.

Having compiled a table of values, you can plot the function y=sin(A-60 o), shown in fig. left. If the y=sinA curve starts at 0 o , then the y=sin(A-60 o ) curve starts at 60 o (ie its zero value is 60 o to the right). Thus, it is said that y=sin(A-60 o) late relative to y=sinA by 60°.
Schedule. y=sin(A-60 o) (sine wave).

Having compiled a table of values, you can plot the function y=cos(A+45 o), shown in fig. below.
If the curve y=cosA starts at 0 o , then the curve y=cos(A+45 o) starts 45 o to the left (ie its zero value is 45 o earlier).
Thus, the plot is said to be y=cos(A+45 o) ahead of plot y=cosA at 45°.
Schedule. y=cos(A+45 o) (cosine).

In general, the graph y=sin(A-α) lags relative to y=sinA by an angle α.
The cosine wave has the same shape as the sinusoid, but starts 90 o to the left, i.e. ahead of her by 90 o . Therefore, cosA=sin(A+90o).

Example 5
Plot y=5sin(A+30 o) in the range from A=0 o to A=360 o

Solution:
Amplitude = 5, period = 360 o /1 = 360 o .
5sin(A+30 o) leads 5sinA by 30 o i.e. starts 30 o earlier.
Graph y=5sin(A+30 o) (sinusoid).

Example 6
Plot y=7sin(2A-π/3) in the range from A=0 o to A=360 o .

Solution:
Amplitude = 7, period = 2π/2= π radians
In general y=sin(pt-α) lags relative to y=sinpt by α/p, therefore 7sin(2A-π/3) lags relative to 7sin2A by (π/3)/2, i.e. per π/6 radians or 30 o

Sinusoid of the form Asin(ωt±α). phase angle. Phase shift.

Let OR in fig. on the left is a vector freely rotating counterclockwise around O at a speed of ω radians/s. The rotating vector is called phase vector. After a time of t seconds, OR will rotate through the angle ωt radians (in the figure on the left, this is the angle TOR). If ST is constructed perpendicular to OR, then sinωt=ST/OT, i.e. ST=OTsinωt.
If all such vertical components are projected onto a plot of y versus ωt, a sinusoid with amplitude OR will be obtained.

If the phase vector OR makes one revolution (i.e. 2π radians) in T seconds, then the angular velocity ω=2π/T rad/s, whence
Т=2π/ ω (s), where
T is period
The number of complete periods that pass in 1 second is called frequency f.
Frequency = (number of periods)/(second) = 1/ T = ω/2π Hz, those. f= ω/2π Hz
Therefore, the angular velocity
ω=2πf rad/s.

If in general the sinusoidal function looks like y=sin(ωt± α), then
A - amplitude
ω - angular velocity
2π/ ω - period T, s
ω/2π - frequency f, Hz
α is the lead or lag angle (relative to y=Аsinωt) in radians, it is also called the phase angle.

Example 7
Alternating current is given as i=20sin(90πt+0.26) amps. Determine amplitude, period, frequency and phase angle (in degrees)

Solution:
i \u003d 20sin (90πt + 0.26) A, therefore,
the amplitude is 20 A
angular velocity ω=90π, therefore,
period T= 2π/ ω = 2π/ 90π = 0.022 s = 22ms
frequency f\u003d 1 / T \u003d 1 / 0.022 \u003d 45.46 Hz
phase angle α= 0.26 rad. \u003d (0.26 * 180 / π) o \u003d 14.9 o.

Example 8
The oscillating mechanism has a maximum displacement of 3 m and a frequency of 55 Hz. At time t=0 the displacement is 100cm. Express the shift in the general form Аsin(ωt± α).

Solution
Amplitude = maximum displacement = 3m
Angular velocity ω=2πf = 2π(55) = 110 rad/s
Therefore, the displacement is 3sin(110πt + α) m.
At t=0 offset = 100cm=1m.
Therefore, 1= 3sin(0 + α), i.e. sinα=1/3=0.33
Therefore α=arcsin0,33=19 o
So the offset is 3sin(110 πt + 0.33).

Example 9
The value of the instantaneous voltage in the AC circuit at any t seconds is given as v=350sin(40πt-0.542)V. Find:
a) Amplitude, period, frequency and phase angle (in degrees)
b) voltage value at t = 0
c) voltage value at t = 10 ms
d) the time it takes for the voltage to reach 200 V for the first time.
Solution:
a) The amplitude is 350 V, the angular velocity is ω=40π
Hence,
period Т=2π/ ω=2π/40π=0.05 s =50ms
frequency f=1/T=1/0.05=20 Hz
phase angle \u003d 0.542 rad (0.542 * 180 / π) \u003d 31 o with a delay relative to v \u003d 350sin (40πt)
b) If t \u003d 0, then v \u003d 350sin (0-0.542) \u003d 350sin (-31 o) \u003d -180.25 V
c) If t \u003d 10 ms, then v \u003d 350sin (40π10 / 10 3 -0.542) \u003d 350sin (0.714) \u003d 350sin41 o \u003d 229.6 V
d) If v=200 AND, then 200=350sin(40πt-0.542) 200/350=sin(40πt-0.542)

Schedule. Oscillating mechanism
(example, sinusoid).

v=350sin(40πt-0.542) Therefore, (40πt-0.542)=arcsin200/350=35 o or 0.611 rad.
40πt= 0.611+0.542=1.153.
Therefore, if v=200V, then time t=1.153/40π=9.179 ms