§ 3.2. .Work on moving a charge in an electrostatic field
A force acts on a charge from the electrostatic field. Therefore, when a charge moves in an electrostatic field, work is done.
The electrostatic field forces are conservative, i.e. the work of the electrostatic field forces to move a charge does not depend on the shape of the path, but is determined only by the position of the starting and ending points of the path. Let's show it. Let a point charge +q 0 move in the field of a stationary point charge +q in a vacuum from point 1 to point 2. Elementary work of the Coulomb force acting on the charge 
charge side 
along the path dl is equal to dA = F dl cosα. According to Coulomb's law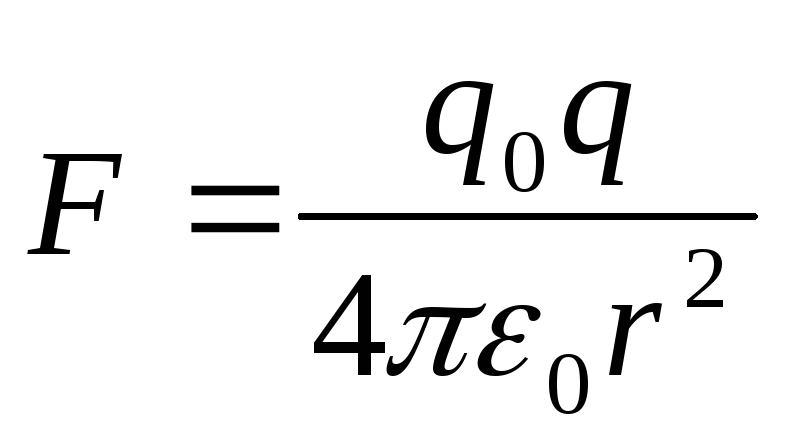 
,dl cosα = dr. Then 
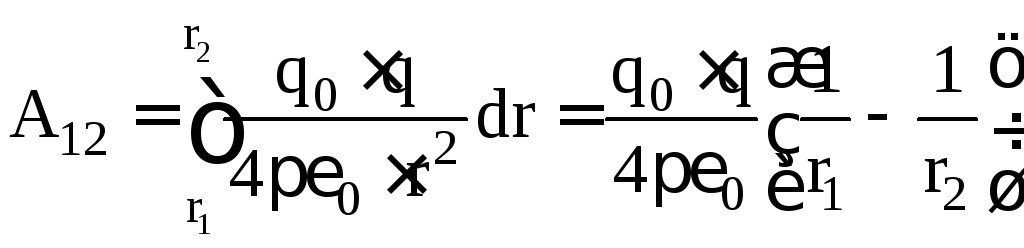. That is, the work is determined only by the position of points 1 and 2.
In mechanics we have determined that:
Conservative are forces whose work does not depend on the shape of the path, but is determined only by the coordinates of the initial and final positions of the material point;
potential field of conservative forces.
For potential fields, you can introduce the concepts of potential and potential difference. Designated by: potential φ, potential difference φ 1 -φ 2. Measured in SI units in volts (V).
The potential of a given point of the electrostatic field is numerically equal to the work of the forces of the electrostatic field to move a unit positive charge from a given point of the field to infinity.
The potential difference φ 1 -φ 2 between points of the electrostatic field (1 and 2) is numerically equal to the work done by the field forces when moving a single positive charge along an arbitrary path from point 1 to point 2.
Previously, a formula was obtained for the work of the field of a point charge q by moving charge q 0 from point 1 to point 2: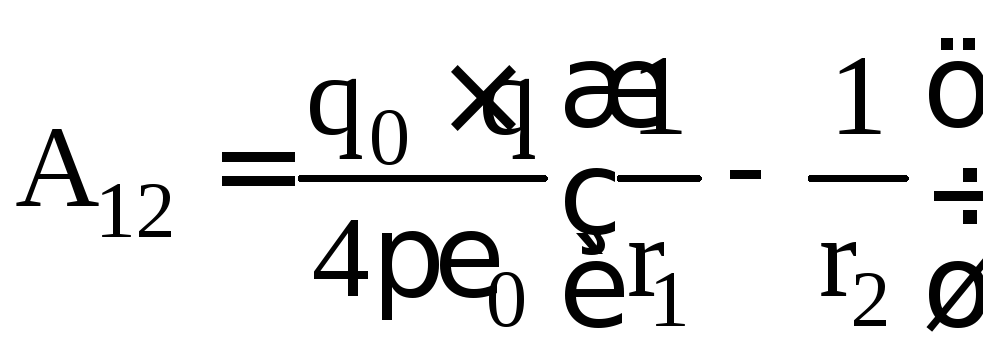 
. On the other hand, the work done by the forces of any electrostatic field when moving a charge q 0 from point 1 to point 2 is equal to A 12 = q 0 . (φ 1 -φ 2). Hence, 
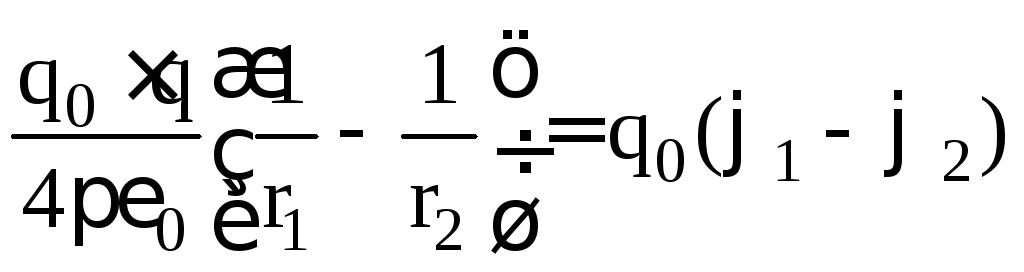. From here we find the expression for the potential of the electrostatic field of a point charge q in vacuum: 
.
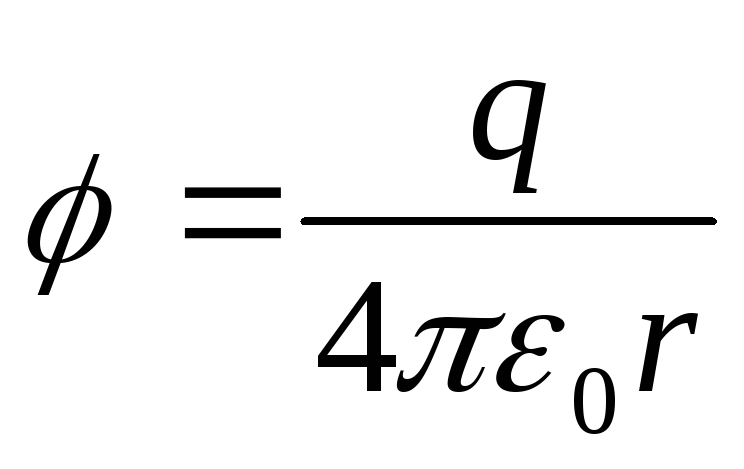The principle of field superposition: the potential of the electrostatic field created by a system of charges is equal to the algebraic sum of the field potentials created by each of these charges separately 
.
Potential charge energy q 0 at a point in an electrostatic field with potential φ: W P = q 0 . φ. This means that potential is an energy characteristic of an electrostatic field.
The electrostatic field is characterized by two quantities: 1) intensity (power characteristic); 2) potential (energy characteristic). It can be assumed that these quantities are somehow related to each other. Let us show that this is so.
Work done by field forces to move charge q 0 along a segment of path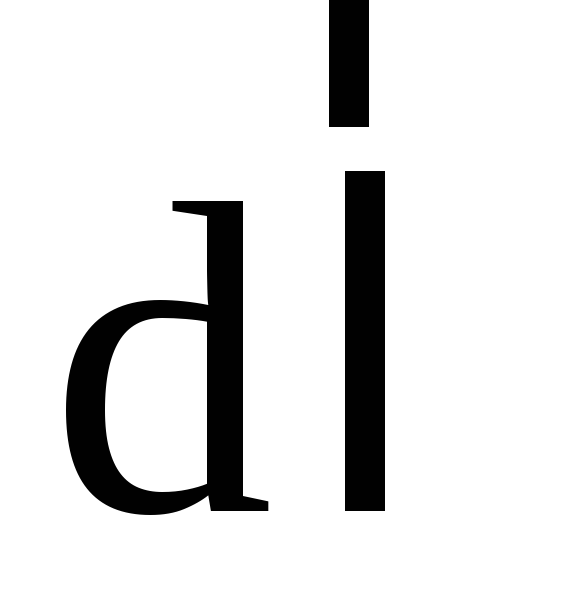 
: , Where 
- vector projection 
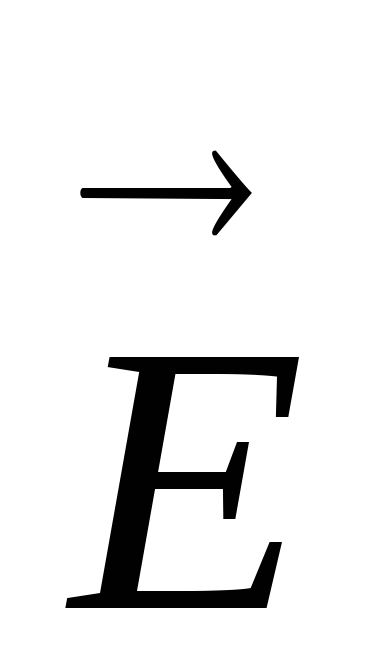to the direction of movement 
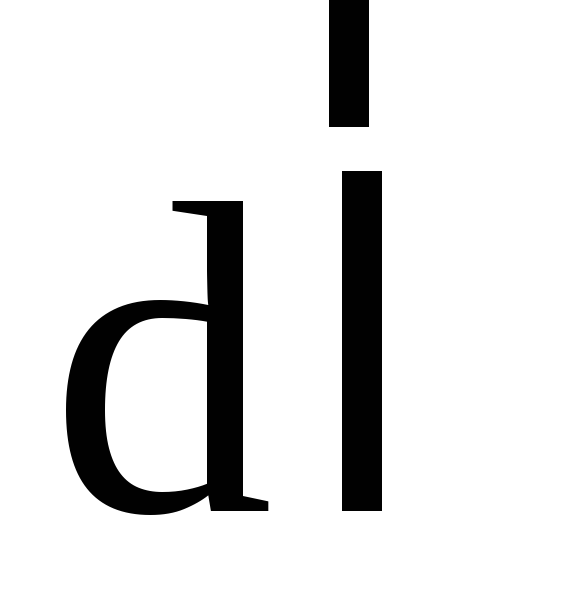. On the other hand, this work will be equal to the decrease in the potential energy of the charge:. Equating the right-hand sides of the expressions for the field operation, we obtain that 
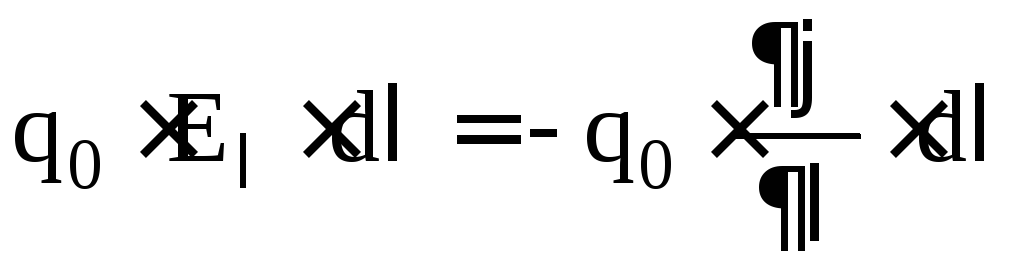, from here 
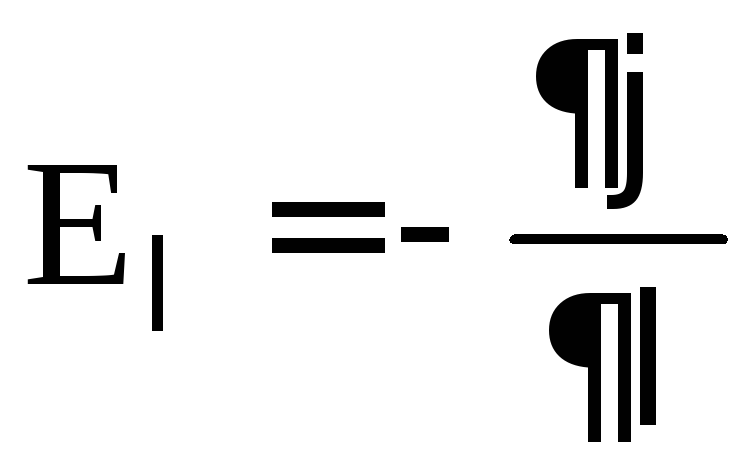, which means: the projection of the electrostatic field strength vector onto some arbitrary direction is equal to the derivative of the potential in this direction with the opposite sign. Here 
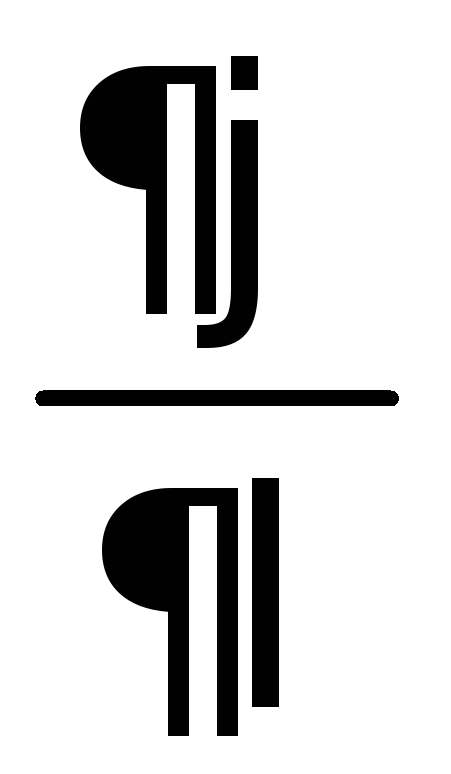- the speed of potential change in a given direction.
Due to the arbitrariness of the choice of direction, we can write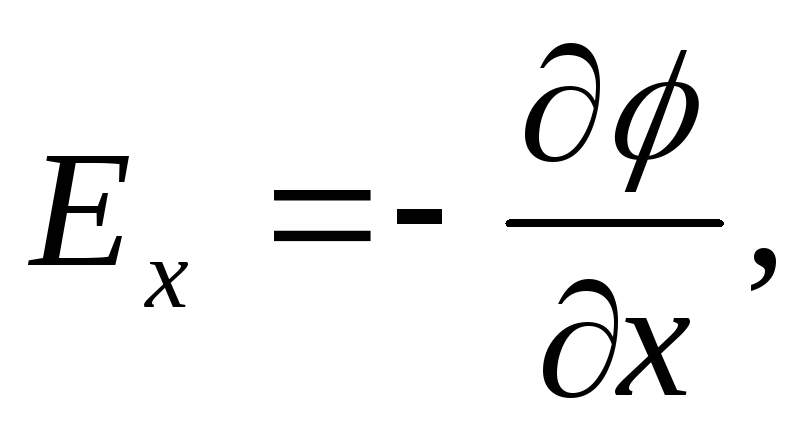 
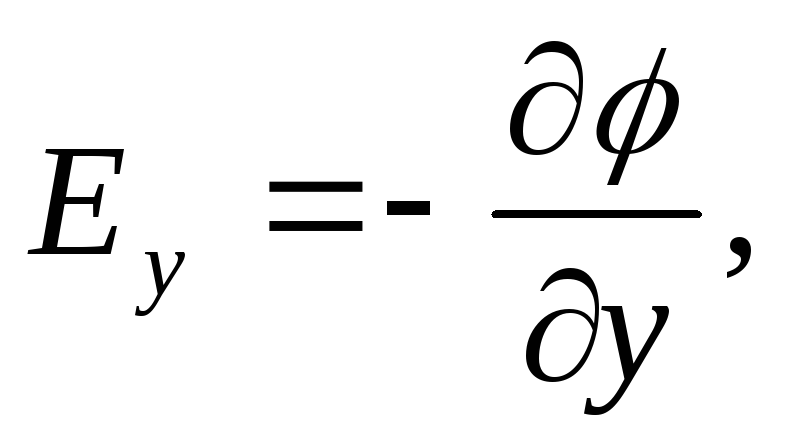
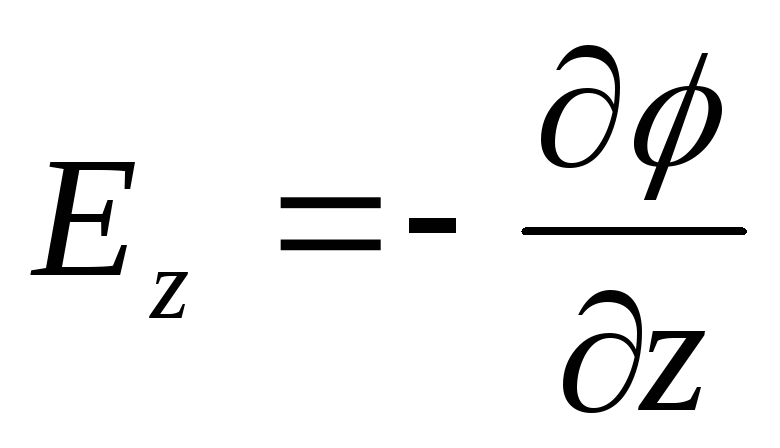, or: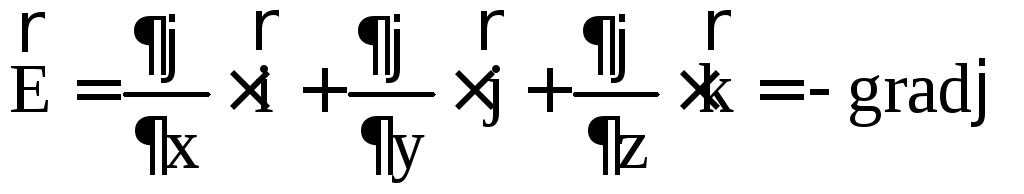 
. This formula expresses the relationship between the strength of the electrostatic field and the potential: the strength of the electrostatic field is equal to the potential gradient, taken with the opposite sign. The minus sign means that the field strength is directed in the direction of decreasing potential.
Thus, if the value of the potential φ at each point of the field is known, then the intensity at each point of the field can be found using the formula 
.It is also possible to solve the inverse problem, i.e. according to given values 
at each point find the potential difference between two arbitrary points of the field using the formula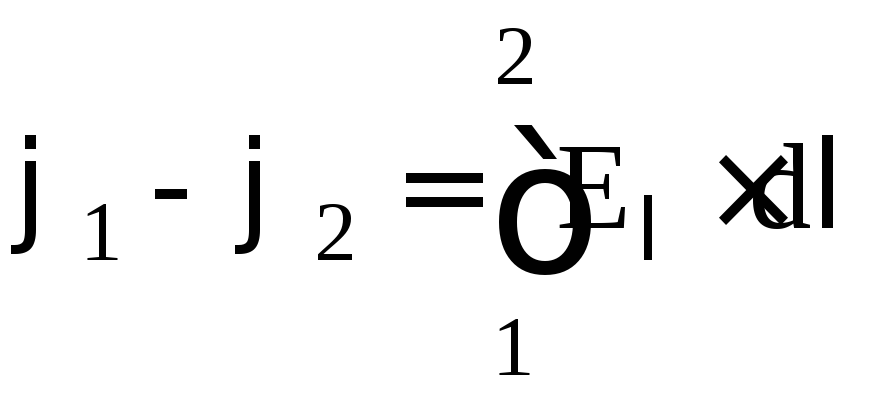 
. The integral can be taken along any line connecting points 1 and 2 (since the work of the electrostatic field forces does not depend on the shape of the path).
For uniform field
or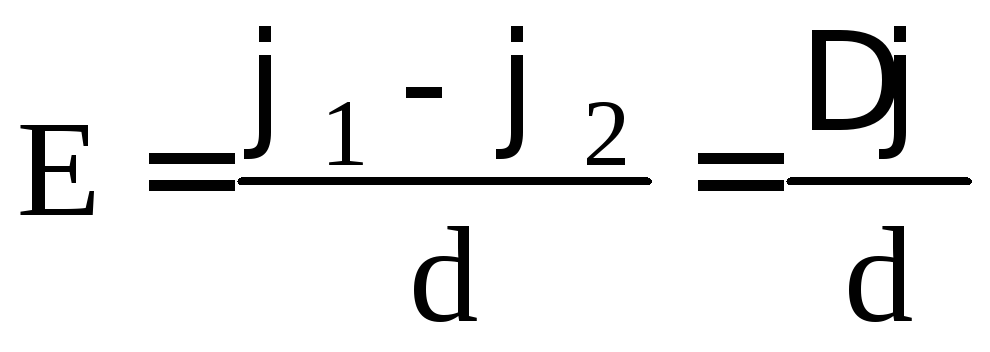 
, where d is the distance between points 1 and 2 along the field line.
Surfaces of equal potential or equipotential surfaces are also used to graphically represent the electrostatic field.
An equipotential surface is a surface on which all points have the same potential.
Equipotential surfaces are drawn so that the potential difference between adjacent surfaces is the same everywhere. Thus, the denser the equipotential surfaces are located, the greater the grad φ in a given place and, therefore, the greater the tension 
.
The field lines are perpendicular to the equipotential surfaces, because the work of moving a charge along an equipotential surface is zero, and, therefore, the force acting on the charge is perpendicular to its movement.
For a uniform field, equipotential surfaces are parallel planes perpendicular to the field lines.
When a charge moves in an electrostatic field, the Coulomb forces acting on the charge do work. Let charge q 0 0 move in the field of charge q0 from point C to point B along an arbitrary trajectory (Fig. 1.12). The Coulomb force acts on q 0
With elementary charge movement d l, this force does work dA
Where is the angle between the vectors and. Quantityd l cos=dr is the projection of the vector onto the direction of the force. Thus, dA=Fdr, . The total work done to move a charge from point C to B is determined by the integral 
, where r 1 and r 2 are the distances of the charge q to points C and B. From the resulting formula it follows that the work done when moving electric charge q 0 in the field of a point charge q, does not depend on the shape of the movement path, but depends only on the starting and ending points of movement
.
In the dynamics section it is shown that a field that satisfies this condition is potential. Therefore, the electrostatic field of a point charge is potential, and the forces acting in it are conservative.
If the charges q and q 0 are of the same sign, then the work of the repulsive forces will be positive when they move away and negative when they approach (in the latter case, the work is performed by external forces). If the charges q and q 0 are opposite, then the work of the attractive forces will be positive when they approach each other and negative when they move away from each other (in the latter case, the work is also performed by external forces).
Let the electrostatic field in which the charge q 0 moves be created by a system of charges q 1, q 2,...,q n. Consequently, independent forces act on q 0 ,
whose resultant is equal to their vector sum. The work A of the resultant force is equal to the algebraic sum of the work of the component forces, 
, where r i 1 and r i 2 are the initial and final distances between charges q i and q 0.
Circulation of the tension vector.
When a charge moves along an arbitrary closed path L, the work done by the electrostatic field forces is zero. Since the final position of the charge is equal to the initial position r 1 =r 2, then (the circle at the integral sign indicates that the integration is carried out along a closed path). So what, then. From here we get. Reducing both sides of the equality by q 0, we obtain or, where E l=Ecos - projection of vector E onto the direction of elementary displacement. The integral is called circulation of the tension vector. Thus, circulation of the electrostatic field strength vector along any closed loop is zero . This conclusion is a condition field potentiality.
Potential charge energy.
In a potential field, bodies have potential energy and the work of conservative forces is done due to the loss of potential energy.
Therefore work A 12 can be represented as the difference in potential charge energies q 0 at the initial and final points of the charge field q :
Potential charge energy q 0 located in the charge field q on distance r equal to
Assuming that when the charge is removed to infinity, the potential energy goes to zero, we get: const = 0 .
For namesake charges potential energy of their interaction ( repulsion) positive, For different names charges potential energy from interaction ( attraction) negative.
If the field is created by the system n point charges, then the potential charge energy q 0 located in this field is equal to the sum of its potential energies created by each of the charges separately:
Electrostatic field potential.
The ratio does not depend on the test charge q0 and is, energy characteristic of the field, calledpotential :
Potential ϕ at any point in the electrostatic field is scalar physical quantity, determined by the potential energy of a unit positive charge placed at this point.
1.7 Relationship between tension and potential.
6. Work when moving an electric charge in electric field
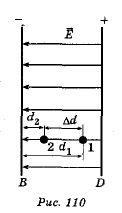
Let's calculate the work done when moving an electric charge in a uniform electric field with intensity . If the charge moved along the field strength line at a distance Ad = d 1 -d 2 (Fig. 110), then the work is equal to
where d 1 and d 2 are the distances from the start and end points to plate B.
In mechanics, it was shown that when moving between two points in a gravitational field, the work done by gravity does not depend on the trajectory of the body. The forces of gravitational and electrostatic interaction have the same dependence on distance; the force vectors are directed along a straight line connecting interacting point bodies. It follows that when a charge moves in an electric field from one point to another, the work of forces electric field does not depend on the trajectory" of its movement.
When the direction of movement changes by 180°, the work of the electric field forces, like the work of gravity, changes sign to the opposite. If, when moving a charge q from point B to point C, the electric field forces did work A, then when moving a charge q along the same path from point C to point B, they do work - A. But since the work does not depend on the trajectory, then and when moving along the SCV trajectory, work is also done - A. It follows that when a charge moves first from point B to point C, and then from point C to point B, i.e. along a closed trajectory, the total work of the electrostatic field forces turns out to be equal to zero (rie.111).
The work done by electrostatic field forces when an electric charge moves along any closed path is zero.
A field whose work of forces along any closed trajectory is zero is called a potential field. Gravitational and electrostatic fields are potential fields.
7. Concept of potential - field potential of a point charge
The electrostatic field potential is a scalar quantity equal to the ratio of the potential energy of a charge in the field to this charge:
Energy characteristics of the field at a given point. The potential does not depend on the amount of charge placed in this field.
because potential energy depends on the choice of coordinate system, then the potential is determined accurate to a constant.
The reference point for the potential is chosen depending on the task: a) the potential of the Earth, b) the potential of an infinitely distant point of the field, c) the potential of the negative plate of the capacitor.
A consequence of the principle of field superposition (potentials add up algebraically).
Electrostatic field potential at a point r is equal to the ratio of the potential energy of a test point charge q" placed at a given point to the value of this charge q".
φ - does not depend on q"!
8.Potential difference. The Relationship Between Tension and Potential
When the values of these two potentials are not equal to each other, a vector difference in the impact and reaction potentials occurs. It determines the direction of movement of energy carriers during energy exchange: from the environment to the system or in the opposite direction. In contrast to the potential difference between the environment and the equilibrium system, there is a local potential difference inside the nonequilibrium system. Therefore, two different definitions should be given: 1. The potential difference in relation to the equilibrium system is the difference between the potential of the system as a whole and the potential of the environment (or the potential of a neighboring system). 2. The potential difference within a nonequilibrium system is the difference between the local potentials of the subsystems within this system. The potential difference is directed from a larger potential to a smaller one; it can be written in the form ΔР 12 = (Р 1 − Р 2) e 12, (3) where Р 1 and Р 2 are the potentials of the system or its environment; e 12 is the unit vector of the direction from the system to the environment or in the opposite direction. In general, the subscripts can be omitted and the notation ΔР can be used. The difference in local potentials is also directed, it can be written in the form ΔР 12 = (Р j1 − Р j2) е 12, (4) where Р j1 and Р j2 are local potentials of different subsystems within a nonequilibrium system; e 12 is the unit vector of the direction from subsystem 1 to subsystem 2.
The Relationship Between Tension and Potential expresses the characteristic of the electric field. Moreover, if tension serves as its power characteristic and allows us to determine the magnitude of the force that acts on the charge at an arbitrary point in this field, then potential is its energy characteristic. Based on the potentials at different points of the electric field, we can determine the amount of work to move the charge using the formulas: A = qU, or A = q(φ₁ - φ₂), where q is the amount of charge, U is the voltage between the points of the field and φ₁, φ₂ is the potential of the points of movement . Let us consider the relationship between tension and potential in a single-valued electric field. The intensity E at any point in such a field is the same, which means that the force F that acts on a unit charge is also the same and equals E. It follows from this that the force that acts on charge q in a given field will be equal to F = qE. If the distance between two points of such a field is equal to d, then when the charge moves, work will be done: A = Fd = gEd = g(φ₁-φ₂), where φ₁-φ₂ is the potential difference between the points of the field. Hence: E= (φ₁-φ₂)/d, i.e. the intensity of a uniform electric field will be equal to the potential difference per unit length taken along the field line of a given field. At short distances, the relationship between intensity and potential is determined similarly in a non-uniform field, since any field between two closely located points can be taken as homogeneous.-
9.Electrical capacity. Capacitor.
Electric capacitance of the capacitor. Physical quantity determined by charge ratio q one of the capacitor plates to the voltage between the capacitor plates is called electrical capacity of the capacitor:. With a constant arrangement of the plates, the electrical capacity of the capacitor is a constant value for any charge on the plates. Unit of electrical capacity. Unit of electrical capacity in the international system - farad(F). An electrical capacitance of 1 F is possessed by a capacitor whose voltage between the plates is equal to 1 V when the plates are charged with opposite charges of 1 C.
Capacitors. The simplest methods of separating unlike electric charges - electrification by contact, electrostatic induction - make it possible to obtain only a relatively small number of free electric charges on the surface of bodies. To accumulate significant quantities of opposite electrical charges, they are used capacitors. Capacitor is a system of two conductors (plates) separated by a dielectric layer, the thickness of which is small compared to the size of the conductors. For example, two flat metal plates located parallel and separated by a dielectric layer form flat capacitor. If the plates of a flat capacitor are given charges of equal magnitude and opposite signs, then the electric field strength between the plates will be twice as strong as the field strength of one plate. Outside the plates, the electric field strength is zero, since equal charges different sign on two plates, electric fields are created outside the plates, the strengths of which are equal in magnitude but opposite in direction
10. Electric dipole
Electric dipole - a system of two equal in magnitude but opposite in sign point electric charges located at some distance from each other.
The distance between charges is called dipole arm.
The main characteristic of a dipole is a vector quantity called electrical torque dipole(P).
Every charge in an electric field is subject to a force that can move that charge. Let us determine the work A of moving a point positive charge from point O to a point performed by the forces of the electric field of a negative charge (Fig. 158). According to Coulomb's law, the force moving a charge is variable and equal to
where is the variable distance between the charges. Note that according to the same law (inversely proportional to the square of the distance), the force moving the mass in the gravitational field of the mass changes (see § 17).
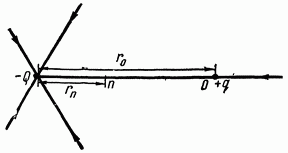
Therefore, the work of moving a charge in an electric field (done by electric forces) will be expressed by a formula similar to the formula for the work of moving a mass in a gravitational field (done by gravitational forces):
Formula (19) is derived in exactly the same way as formula (8) was derived in § 17.
Formula (19) can be derived even more simply by integration:
The minus sign in front of the integral is due to the fact that for approaching charges the value is negative, while the work should be positive, since the charge moves in the direction of the force.
Comparing formula (19) with general formula(4) from § 17, we come to the conclusion that the quantity represents the potential energy of the charge at a given point in the electric field:
The minus sign shows that as the charge is moved by field forces, its potential energy decreases, turning into the work of movement. Magnitude
equal to the potential energy of a unit positive charge is called the electric field potential or electric potential. Electric potential does not depend on the magnitude of the transferred charge and therefore can serve as a characteristic of the electric field, just as the gravitational potential serves as a characteristic of the gravitational field.
Substituting the potential expression (21) into the work formula (19), we obtain
Assuming we get
Thus, the potential difference between two points of the field is equal to the work of the field forces to move a unit positive charge from one point to another.
Let us now move the charge (acting against the field forces) from a certain point to infinity. Then, according to formulas (21) and (23), and
When we get Therefore, the potential of a point of the electric field is equal to the work of moving a unit positive charge from a given point to infinity.
From formula (24) we establish a unit of measurement of potential called volt (V):
i.e., a volt is the potential of such a point in the field, when moving from which a charge “and infinity, work is done in Dimension of potential
Now, taking into account formula (25), it can be shown that the unit of measurement of electric field strength established in § 75 is indeed equal to
If the charge creating the field is negative, then the field forces prevent the movement of a single positive charge to infinity, thereby doing negative work. Therefore, the potential of any point in the field created by a negative charge is negative (just as the gravitational potential of any point in the gravitational field is negative). If the charge creating the field is positive, then the field forces themselves move a unit positive charge to infinity, doing positive work. Therefore, the potential of any point in the field of a positive charge is positive. Based on these considerations, we can write expression (21) in a more general form:
where the minus sign refers to the case of a negative charge, and the plus sign to the case of a positive charge
If a field is created by several charges, then its potential is equal to the algebraic sum of the field potentials of all these charges (potential is a scalar quantity: the ratio of work to charge). Therefore, the field potential of any charged system can be calculated based on the formulas given earlier, after first dividing the system into a large number of point charges.
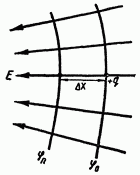
The work of moving a charge in an electric field, like the work of moving mass in a gravitational field, does not depend on the shape of the path, but depends only on the potential difference between the starting and ending points of the path. Consequently, electric forces are potential forces (see § 17). A surface at all points of which the potential is the same is called equipotential. From formula (22) it follows that the work of moving a charge along an equipotential surface is zero (since this means that the electric field forces are directed perpendicular to the equipotential surfaces, i.e., the field lines are perpendicular to the equipotential surfaces (Fig. 159).
When moving the test charge q In an electric field, electric forces do work. This work for small displacement is equal to (Fig. 1.4.1):
Let us consider the work of forces in an electric field created by a distributed charge that does not change in time, i.e. electrostatic field
The electrostatic field has an important property:
The work of electrostatic field forces when moving a charge from one point in the field to another does not depend on the shape of the trajectory, but is determined only by the position of the starting and ending points and the magnitude of the charge.
The gravitational field also has a similar property, and this is not surprising, since gravitational and Coulomb forces are described by the same relations.
A consequence of the independence of work from the shape of the trajectory is the following statement:
The work done by the electrostatic field forces when moving a charge along any closed trajectory is zero.
Force fields that have this property are called potential or conservative .
In Fig. 1.4.2 shows the field lines of the Coulomb field of a point charge Q and two different trajectories of test charge movement q from the starting point (1) to the ending point (2). On one of the trajectories a small displacement Work Δ is highlighted A Coulomb forces on this displacement is equal to
The obtained result does not depend on the shape of the trajectory. On trajectories I and II shown in Fig. 1.4.2, the work of the Coulomb forces is the same. If you change the direction of charge movement on one of the trajectories q to the opposite, then the work will change sign. It follows that on a closed trajectory the work of Coulomb forces is equal to zero.
If the electrostatic field is created by a set of point charges, then when the test charge moves q Job A the resulting field, in accordance with the superposition principle, will consist of the work of the Coulomb fields of point charges: Since each term of the sum does not depend on the shape of the trajectory, the total work A The resulting field is independent of the path and is determined only by the position of the starting and ending points.
The potentiality property of the electrostatic field allows us to introduce the concept potential energy charge in an electric field. To do this, a certain point (0) is selected in space, and the potential energy of the charge q, placed at this point, is taken equal to zero.
Potential charge energyq , placed at any point (1) of space, relative to a fixed point (0) is equal to workA 10 , which the electrostatic field will make when moving a chargeq from point (1) to point (0):
|
(In electrostatics, energy is usually denoted by the letter W, since the letter E denote the field strength.)
Just as in mechanics, potential energy is determined up to a constant value, depending on the choice of the reference point (0). Such ambiguity in the definition of potential energy does not lead to any misunderstandings, since physical meaning has not the potential energy itself, but the difference in its values at two points in space.
Work done by an electrostatic field when moving a point chargeq from point (1) to point (2), is equal to the difference in the potential energy values at these points and does not depend on the path of charge movement and on the choice of point (0).
Potential φ is an energy characteristic of an electrostatic field.
Job A 12 on the movement of electric charge q from the starting point (1) to the ending point (2) is equal to the product of the charge and potential difference (φ 1 – φ 2) start and end points:
In many problems of electrostatics, when calculating potentials, it is convenient to take the point at infinity as the reference point (0). In this case, the concept of potential can be defined as follows:
The field potential at a given point in space is equal to the work done by electric forces when removing a unit positive charge from a given point to infinity.
As follows from Gauss’s theorem, the same formula expresses the field potential of a uniformly charged ball (or sphere) at r ≥ R, Where R– radius of the ball.
For a visual representation, electrostatic fields along with lines of force are used equipotential surfaces.
A surface at all points of which the electric field potential has the same values is calledequipotential surface orsurface of equal potential .
Electrostatic field lines are always perpendicular to equipotential surfaces.
The equipotential surfaces of the Coulomb field of a point charge are concentric spheres. In Fig. 1.4.3 shows pictures of field lines and equipotential surfaces of some simple electrostatic fields.
In the case of a uniform field, equipotential surfaces are a system of parallel planes.
If the test charge q committed small movement along the force line from point (1) to point (2), then we can write:
This relationship expresses in scalar form the relationship between field strength and potential. Here l– coordinate measured along the field line.
From the principle of superposition of field strengths created by electric charges, the principle of superposition for potentials follows:
Equipotential surfaces- a concept applicable to any potential vector field, for example, a static electric field or a Newtonian gravitational field. An equipotential surface is a surface on which the scalar potential of a given potential field takes on a constant value (potential level surface). Another, equivalent, definition is a surface that is orthogonal to the field lines at any point.
The surface of a conductor in electrostatics is an equipotential surface. In addition, placing a conductor on an equipotential surface does not change the configuration of the electrostatic field. This fact is used in the image method, which allows the calculation of the electrostatic field for complex configurations.
In a (stationary) gravitational field, the level of a stationary fluid is established along the equipotential surface. In particular, it can be approximately stated that the level of the oceans passes along the equipotential surface of the Earth’s gravitational field. The shape of the surface of the oceans, extended to the surface of the Earth, is called the geoid and plays an important role in geodesy. The geoid is thus an equipotential surface of gravity, consisting of a gravitational and a centrifugal component.
EQUIPOTENTIAL LINES
Lines of equal potential values of the electric field being studied.
