Stairs. Entry group. Materials. Doors. Locks. Design

The potential difference between the ends of the rod will be equal in magnitude to the induced emf arising in the rod due to rotation

. (1)

For homogeneous magnetic field and flat surface dФ m = BdScosa, or, substituting in (1), we get (we omit the minus sign, since it is necessary to find only the value of the emf)

. (2)

According to the conditions of the problem cosa=1, therefore from expression (2) it follows

, (3)

dj = wdt = (2pn)dt. (4)

Substituting (4) into (3), we get:

.

U= 10 –3 ×2p×2 (1.2 2 + 2×1.2×0.25)/2 = 0.0128 V = 12.8 mV.

7. Straight conductor length l=10 cm placed in a uniform magnetic field with induction IN=1 T. The ends of the conductor are closed by a flexible wire located outside the field. External circuit resistance R=0.4 Ohm. What power will be required to move the conductor perpendicular to the induction lines at a constant speed u=20 m/s?

Solution

Let us analyze the conditions of the problem. When moving, the conductor will cross the induction lines. Due to this, an induced emf will arise in the conductor

e = – dФ/dt, (1)

where in in this case

dФ = BdS = Bludt . (2)

Substituting (2) into (1), we get:

e = – Blu.

The strength of the induction current in the circuit according to Ohm's law

I = e / R = – (Blv)/R.

Thermal power, allocated at the external resistance

P = I 2 R = B 2 l 2 u 2 /R.

This power will be equal to the power that must be supplied to the system due to external force, acting on the conductor, so that the speed of movement of the conductor is constant. Thus:

P = B 2 l 2 u 2 /R= 1×0.01×400/0.4 = 10 W.

8. Two coils are wound evenly on a cylindrical core, the length of which is much greater than the diameter. The inductance of the first coil is 0.2 H, the second is 0.8 H. The resistance of the second coil is 600 Ohms. What current will flow through the second coil if the current of 0.3 A flowing in the first coil is turned off for a time of 0.001 s.

Solution

This problem belongs to the section of mutual induction. Current strength in the secondary winding

I 2 = e 2 /R 2. (1)

Magnitude e 2 depends on mutual inductance L 12 and the rate of change in current strength I 1

e 2 = –L 12 dI 1 /dt = –L 12 DI 1 /Dt = –L 12 (I 1 – I 01)/Dt. (2)

The mutual inductance of two solenoids having a common core is calculated by the formula

L 12 = mm 0 n 1 n 2 lS. (3)

Self-inductances

L 1 = mm 0 n 1 2 lS, (4)

L 2 = mm 0 n 2 2 lS, (5)

therefore, taking into account expressions (3), (4), (5), we obtain

L 12 = . (6)

Substituting expression (6) into expression (2), and the resulting result into expression (1), we obtain:

I 2 = (L 12 I 01)/R 2 = (I 01 )/R 2 Dt.

I 2= = 0.2 A.

9. On a square toroid cross section 1000 turns of wire are wound. The internal radius of the toroid is 0.1 cm, the external radius is 0.2 cm. The magnetic permeability of the toroid is 100. An electric current with a force of 1 À flows through the toroid winding. Determine the energy of the magnetic field inside the toroid.

Solution

Let's solve the problem in two ways.

1. Magnetic field energy is the energy stored in inductance:

Where L- inductance, I- the strength of the current flowing in the inductance.

The flux linkage, according to the definition of inductance, is calculated as

Y = LI, Y = NF m,

Where Ф m- magnetic flux through the cross section S toroid.

,

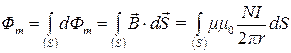Where r- distance from the center of the toroid to the site dS, on which the magnitude of the magnetic field induction is determined. Since the toroid square section, then the height of the platform h = (r 2 - r 1), and the width is dr. That's why

Then the inductance of the toroid

L= = mm 0 N 2 (r 2 - r 1) ln.

Substituting the expression for inductance into the expression for energy, we obtain m is not specified, but it is indicated that the toroid is an iron, steel or cast iron core, then the quantity m is on the dependence graph B = B(H)(adj. 1) as

m = V/m 0 N.

As a quantity N take value N at the central point of the cross section of the toroid.

Physics problems, partII

1. An electron rotates in a circular orbit around a proton. Find the strength of their electrical interaction if the average radius of the electron orbit is equal to 10 -8 see Cl.

2. Two small balls with charges q 1 = 4nKl And q 2 = 2nKl are at a distance 60 cm from each other. Determine tension E electrostatic field at a point lying midway between them.

3. Point charge + q is located at the center of the spherical surface. If you increase its radius, then the vector flow through the surface of the sphere: a) will not change; b) will increase; c) will decrease

4. The electric field strength at the Earth's surface is on average E = 130 V/m. Determine the charge of the Earth, assuming that it has the shape of a sphere with a radius 6400 km.

5. What is the potential difference between two points of the electrostatic field if, when moving a charge between them q = 0.012 Cl work was done by the field A = 0.36 J?

6. An electrostatic field is created by a positive point charge. Determine the numerical value and direction of the potential gradient of this field if at a distance r = 10 cm from charge potential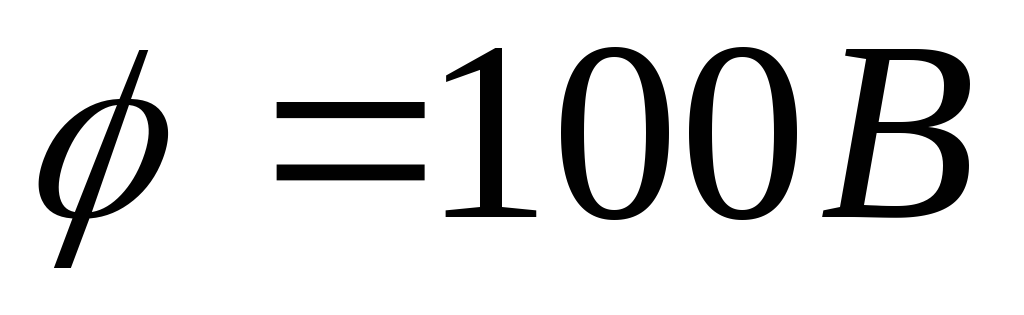

.

7. The space between the plates of a flat-plate capacitor is filled with glass (

).Distance between plates d = 5 mm, potential difference U = 1 kV. Determine: 1) field strength in glass; 2) surface charge density on the capacitor plates.

8. Three capacitors are connected as shown in the figure, where U AB = 250 V, WITH 1 = 1.5 µF, WITH 2 = 3 µF, WITH 3 = 4 µF. What charge and what energy is stored in this bank of capacitors?

9. The current strength in the conductor increases uniformly from 0 before 2A during 2 s. Determine the charge passing through the conductor during this time.

10. Current density in a conductor of length 25 m and resistivity

Ohm∙m wound 4 . Determine the potential difference at the ends of the conductor.

11. In the circuit in the figure, the ammeter shows the current strength

= 1.5A. Current flowing through resistance R 1 , is equal = 0.5 A. Resistance R 2 = 2 ohm, R 3 = 6 ohm. Determine resistance R 1 , as well as current strength And 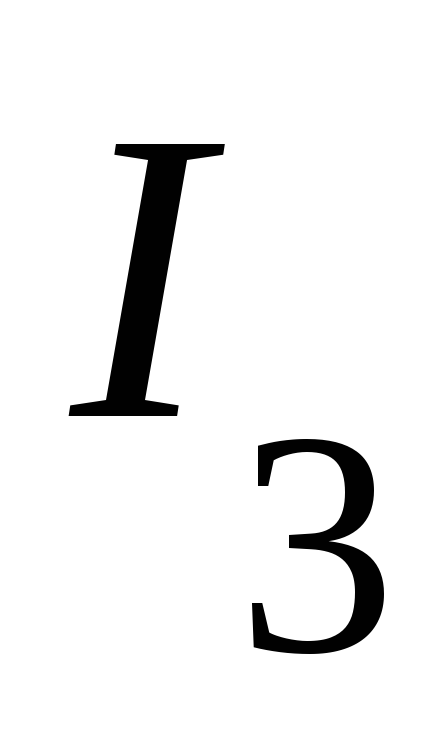through resistance R 2 And R 3 .

12. Batteries with EMF 11.2 V and internal resistance 0.3Ohm charged by current 4 A. What does a voltmeter connected to the battery poles indicate?

13. The electromotive force of the battery is 20 V. Efficiency at current strength 4 A equals 0,8 . What is the internal resistance of the battery?

14. How much heat will be released in the conductor by resistance 100Ohm behind 30 sec, if the current strength in it decreases uniformly from = 10A before = 0 ?

15. Density electric current in a copper wire is equal to 10 A/cm 2 . Determine the specific thermal power of the current if the resistivity of copper is equal to 17 nΩ∙m.

16. Currents flow through two infinitely long straight parallel wires = 40 A And = 80 A same direction. Distance between wires d = 20 cm. Determine magnetic induction IN fields at a point located in the middle between the wires.

17. An electron moves in a uniform magnetic field with induction 0.1 T around the circumference. Determine the angular velocity of electron rotation.

kg,

Cl.

18. Straight wire length 10 cm, through which a current flows 20A 0.01 T. What is the angle between the direction of the field and the direction of the current if a force acts on the wire 10 mN.

19. In a uniform magnetic field with induction 0.1 T. placed a square frame with an area 25 cm 2 . The normal to the plane of the frame makes an angle with the direction of the magnetic field 60 º . Determine the torque acting on the frame if current flows through it 1A.

20. Determine the magnetic induction in the center of a circular wire coil of radius

10 cm, through which current flows 1A.

21. A current flows through a straight infinitely long wire 10A. Determine using the vector circulation theorem , magnetic induction at a point located at a distance 10 cm from the wire.

22. Determine the speed of a charged particle moving along a straight path perpendicular to electric waves crossed at right angles ( E = 400 kV/m) and magnetic ( IN = 0.25 T) fields.

23. A flat contour whose area 25 cm 2 , is in a uniform magnetic field with induction 0.04 T. Determine the magnetic flux penetrating the circuit if its plane makes an angle with the field lines 30 º .

24. The car is traveling at speed 120 km/h. Determine the potential difference at the ends of the front axle of the car if the length of the axle 180 cm, and the vertical component of the Earth's magnetic field strength is equal to 40 .

25. Magnetic field induction between the poles of a two-pole generator V = 0.8 T. The rotor has N = 100 turns area S= 400 cm 2 . How many revolutions does the armature make if the maximum value of the induced emf ε max =200V?

26. Frame containing 25 turns, is in a magnetic field. Determine the induced emf that occurs in the frame when the magnetic flux in it changes from 0.093 Wb before 0.013 Wb behind 0.16 sec.

27. The figure shows the dependence of the magnetic flux penetrating a certain closed loop on time. At what time interval is the induced emf maximum? Minimal?

28. Current flows through the solenoid = 2A. The magnetic flux passing through the cross section of the solenoid is equal to

4 µWb. Determine the inductance of the solenoid if it has 800 turns.

29. Two coils with inductors

L 1 = 0.12 Gn And L 2 = 3 Gn wound on one core. Determine the current strength in the second coil if the current strength in the first coil is 0.01 s. decreases from 0.5 A to zero. Second coil resistance 300 Ohm.

30. A toroid without a core contains 20 turns per 1 cm length. Determine the volumetric energy density of the magnetic field in the toroid if current flows through its winding 3A.

This page has not been proofread

Ohm's law

The reason that causes the movement of electrons along a conductor, that is, the appearance of an electric current, is the potential difference between the ends of the conductor. Therefore, the role of any source of electricity that produces electric current is reduced to maintaining a certain potential difference at the ends of the conductor connected to the source. At the same time, the potential difference also determines the strength of the electric current flowing to the nonconductor. The greater the potential difference at the ends of a conductor, the stronger the electric current in that conductor.

The strength of the electric current in a conductor depends not only on the potential at its ends, but on the properties of the conductor itself, namely on the value of its electrical resistance. The greater the resistance of the conductor, the less the current strength in it will be at the same potential difference across the coils and pipes. These two dependencies together connect three quantities that characterize a conductor with electric current - the potential difference at its ends, its resistance and current strength in it. If two of these quantities are known, then determining the third is not difficult. The relationship between potential difference, resistance and current has been established famous physicist Ohm and is therefore called “Ohm’s law”.

Electrical units

So, Ohm's law determines the real potential differences, resistance and current strength for any conductor. But in order to use this law, you need to be able to measure the quantities that it determines. In other words, you need to choose units to measure these quantities. Most often, the so-called “practical system” of electrical units is used to measure them. In this system, the measure (unit) of potential difference is

“volt”, a measure of resistance “ohm” and a measure of current “ampere” 1).

These units are chosen - volts, ohms and amperes - in such a way that with a potential difference at the ends of the conductor of 1 volt and a conductor resistance of 1 ohm, the current strength in it is exactly equal to 1 ampere. You can determine any of these quantities for another case using Ohm's law. For example, if with a potential difference of 1 volt, the resistance of the conductor is not 1 ohm, but 1) times greater, that is, 10 ohms, then according to Ohm’s law, the current strength in the conductor will be 10 times less, that is, Vio amperes. If, with the same resistance of 10 ohms, we increase the potential difference from 1 to 100 volts, that is, 100 times, then the current strength will increase by 100 times, that is, it will be equal to 10 amperes.

Mathematical expression of Ohm's law

If we instead certain numbers For the sake of generality, we will use letter notation2), then Ohm’s law can be expressed in this way. Let the potential difference at the ends of the conductor be V volts. If the resistance of the conductor were equal to one ohm, then

The current sieve in the conductor would be V ampere. But if the resistance of the conductor is not one, but 1 ohm, then the current strength in the conductor will be R times less, that is,

divided by R amps).

And if we denote this current strength by J, then the current strength in the pro-

Vodnik-J amp. =

This is the mathematical expression of Ohm's law. This means that in order to obtain the current in amperes, you need

potential difference in volts divided by resistance in ohms. Obviously, if we want to determine the difference

1) All these names, as well as the names of other electrical units, are the names of physical scientists who studied electrical phenomena.

2) See the article “Amateur Radio Mathematics”.

potentials at the ends of the conductor, and its resistance and current strength in it are known, then you need to multiply the current strength by the resistance, that is, V volt = 1 amp XR ohm.

This means that the potential difference at the ends of the conductor in volts is equal to the current in the conductor in amperes multiplied by the resistance of the conductor in ohms. This is another formulation of the same Ohm's law.

In practice, instead of the name “potential difference”), the shorter and therefore more convenient name “voltage” is often used. Of course, voltage, like potential difference, is measured in volts.

So, Ohm's law gives the relationship between the voltage at the ends of the conductor, its resistance and the current strength in it. Without missing two of these quantities, we can always determine the third using Ohm's law.

Metric system of units

When measuring various quantities, it is always convenient to use units that are close in size to the dimensions of the quantity being measured. For example, although a meter is taken as a measure of length, it is inconvenient to measure the distance between two cities in meters - it would turn out too big numbers. In this case, it is much more convenient to use a larger measure - a kilometer, equal to a thousand meters. It is also inconvenient to measure the thickness of the wire in meters; the result would be very small fractions of a meter. It is convenient for this purpose to use a smaller measure—a millimeter—a thousandth of a meter.

They do exactly the same thing when electrical measurements. To measure large quantities, use a large measure, and to measure small quantities, use a small measure. These major and minor units are obtained in the same way as in the regular metric system. The prefix “kilo” means a measure a thousand times greater, for example “kilovolt” is a thousand volts. Console. “mega” means a measure a million times greater, for example “megom” is a million ohms. The prefix “milli” means a measure a thousand times smaller, for example “millivolt” is a thousandth of a volt. The prefix “micro” denotes a measure a million times smaller, for example “microampere” is a millionth of an ampere, etc.