The most important law of electrical engineering is Ohm's law
Joule-Lenz law
Joule-Lenz law
In verbal formulation it sounds like this - The power of heat released per unit volume of a medium during flow electric current, is proportional to the product of the electric current density and the value electric field
Where w- heat generation power per unit volume, - electric current density, - electric field strength, σ
- conductivity of the medium.
The law can also be formulated in integral form for the case of current flow in thin wires:
The amount of heat released per unit time in the section of the circuit under consideration is proportional to the product of the square of the current in this section and the resistance of the section
In mathematical form, this law looks like:
Where dQ- the amount of heat released over a period of time dt,I- current strength, R- resistance, Q- the total amount of heat released during the period of time from t1 before t2.
When force constants current and resistance:
Kirchhoff's laws
Kirchhoff's laws (or Kirchhoff's rules) are relationships that hold between currents and voltages in sections of any electrical circuit. Kirchhoff's rules allow you to calculate any electrical circuits of direct and quasi-stationary current. They are of particular importance in electrical engineering because of their versatility, as they are suitable for solving any electrical problems. Application of Kirchhoff's rules to the circuit allows us to obtain the system linear equations relative to the currents, and accordingly, find the value of the currents on all branches of the circuit.
To formulate Kirchhoff's laws, nodes are identified in the electrical circuit - points connection of three and more conductors and circuits - closed paths of conductors. In this case, each conductor can be included in several circuits.
In this case, the laws are formulated as follows.
First law(ZTK, Kirchhoff's Law of Currents) states that the algebraic sum of currents in any node of any circuit is equal to zero (the values of the flowing currents are taken with the opposite sign):
In other words, as much current flows into a node, as much flows out of it. This law follows from the law of conservation of charge. If the chain contains p nodes, then it is described p − 1 current equations. This law can also be applied to other physical phenomena (for example, water pipes), where there is a law of conservation of quantity and the flow of this quantity.
Second Law(ZNK, Kirchhoff's Stress Law) states that the algebraic sum of the voltage drops along any closed contour of the circuit is equal to the algebraic sum of the emf acting along the same contour. If there is no EMF in the circuit, then the total voltage drop is zero:
For constant voltages: 
For alternating voltages:
In other words, when going around the circuit along the circuit, the potential, changing, returns to its original value. If a circuit contains branches, of which the branches contain current sources in the amount of , then it is described by voltage equations. A special case of the second rule for a circuit consisting of one circuit is Ohm's law for this circuit.
Kirchhoff's laws are valid for linear and nonlinear circuits for any type of change in currents and voltages over time.
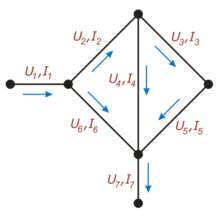
In this figure, for each conductor, the current flowing through it is indicated (the letter “I”) and the voltage between the nodes it connects (the letter “U”)
For example, for the circuit shown in the figure, in accordance with the first law, the following relationships are satisfied:
Note that for each node the positive direction must be chosen, for example here, currents flowing into a node are considered positive and currents flowing out are considered negative.
In accordance with the second law, the following relations are valid:
If the direction of the current coincides with the direction of bypassing the circuit (which is chosen arbitrarily), the voltage drop is considered positive, otherwise - negative.
Kirchhoff's laws, written for nodes and circuit circuits, give complete system linear equations, which allows you to find all currents and voltages.
There is an opinion according to which “Kirchhoff’s Laws” should be called “Kirchhoff’s Rules”, because they do not reflect fundamental entities nature (and are not a generalization large quantity experimental data), but can be deduced from other provisions and assumptions.
LAW OF TOTAL CURRENT
LAW OF TOTAL CURRENT one of the fundamental laws electro magnetic field. Establishes the relationship between magnetic force and the amount of current passing through a surface. The total current is understood as the algebraic sum of currents penetrating a surface bounded by a closed loop.
The magnetizing force along a contour is equal to the total current passing through the surface bounded by this contour. In general, the field strength is various areas magnetic line may have different meanings, and then the magnetizing force will be equal to the sum of the magnetizing forces of each line.
Joule-Lenz law
Joule-Lenz law- a physical law that gives a quantitative estimate thermal action electric current. Discovered in 1840 independently by James Joule and Emilius Lenz.
In verbal formulation it sounds like this:
The power of heat released per unit volume of a medium during the flow of electric current is proportional to the product of the electric current density and the electric field value
Mathematically can be expressed in the following form:
Where w- power of heat release per unit volume, - electric current density, - electric field strength, σ - conductivity of the medium.
LAW OF ELECTROMAGNETIC INDUCTION, Faraday's law is a law that establishes the relationship between magnetic and electrical phenomena. EMF electromagnetic induction in a contour is numerically equal and opposite in sign to the rate of change of magnetic flux through the surface bounded by this contour. The magnitude of the EMF field depends on the rate of change of the magnetic flux.
FARADAY'S LAWS(named after the English physicist M. Faraday (1791-1867)) – the basic laws of electrolysis.
A relationship is established between the amount of electricity passing through an electrically conductive solution (electrolyte) and the amount of substance released at the electrodes.
When passed through an electrolyte direct current I within a second q = It, m = kIt.
Faraday's second law: the electrochemical equivalents of elements are directly proportional to their chemical equivalents.
Gimlet rule
Gimlet's rule(also, rule right hand) - a mnemonic rule for determining the direction of the angular velocity vector, characterizing the speed of rotation of the body, as well as the magnetic induction vector B or to determine the direction of the induction current.
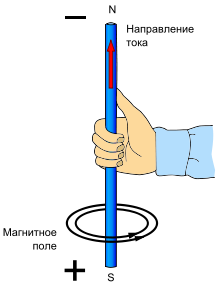
Right hand rule
Right hand rule
Gimlet rule: “If the direction of translational movement of the gimlet (screw) coincides with the direction of the current in the conductor, then the direction of rotation of the gimlet handle coincides with the direction of the magnetic induction vector.”
Determines the direction of the induction current in a conductor moving in a magnetic field
Right hand rule: “If the palm of the right hand is positioned so that it includes power lines magnetic field, and direct the bent thumb along the movement of the conductor, then four extended fingers will indicate the direction of the induction current.”
For solenoid it is formulated as follows: “If you clasp the solenoid with the palm of your right hand so that four fingers are directed along the current in the turns, then the extended thumb will show the direction of the magnetic field lines inside the solenoid.”
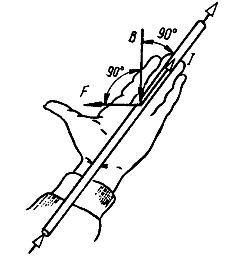
Left hand rule
Left hand rule
If the charge is moving and the magnet is at rest, then the left-hand rule applies to determine the force: “If left hand positioned so that the magnetic field induction lines enter the palm perpendicular to it, and the four fingers are directed along the current (along the movement of a positively charged particle or against the movement of a negatively charged one), then the thumb set at 90° will show the direction of the acting Lorentz or Ampere force.”
Fedun V.I. Lecture notes on physics Electromagnetics
Lecture 26.
Electromagnetic induction. Faraday's discovery .
In 1831, M. Faraday made one of the most important fundamental discoveries in electrodynamics - the phenomenon was discovered electromagnetic induction .
In a closed conducting circuit, when the magnetic flux (vector flux) covered by this circuit changes, an electric current arises.
This current is called induction .
The appearance of induction current means that when the magnetic field changes
|
|
flow in the circuit occurs e.m.f. |
|
Changing the sign of the derivative |
leads to a change in sign
Figure 26.1. 
Faraday discovered that an induced current can be produced in two different ways, which can be conveniently explained by means of a diagram. 
1st method: moving the frame
in the magnetic field of a stationary coil 
(see Fig. 26.1). 2nd method: changing the magnetic field 
, created by the coil , due to its movement or due to changes in current strength
in it (or both together). Frame 
while still motionless. .
In both these cases the galvanometer 
will indicate the presence of induction current in the frame
The direction of the induction current and, accordingly, the sign of the emf. induction
are determined by Lenz's rule. .
Lenz's rule. The induced current is always directed so as to counteract the cause that causes it .
Whatever the reason for the change in the magnetic flux covered by a closed conducting circuit, arising in the emf circuit. induction is given by the formula
|
|
The nature of electromagnetic induction.
In order to clarify the physical reasons that lead to the emergence of emf. By induction, we consider two cases successively.
act force
The electromotive force created by this field is called electromotive force of induction
. In our case
|
|
The minus sign is placed here because the third-party field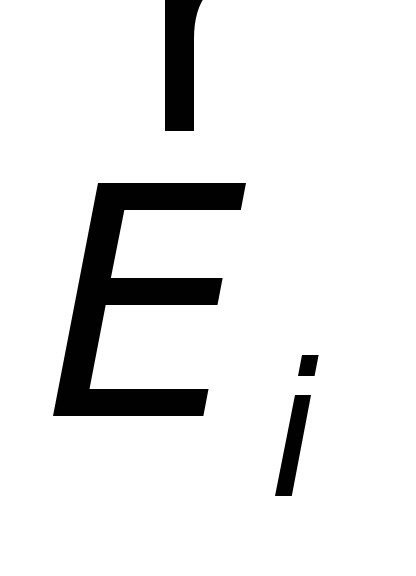 
directed against the positive bypass of the circuit determined by the right screw rule. Work 
is the rate of increase in the contour area (increase in area per unit time), therefore
|
|
Where 
- increment of magnetic flux through the circuit.
|
|
The obtained result can be generalized to the case of arbitrary orientation of the magnetic field induction vector relative to the contour plane and to any contour moving (and/or deforming) in an arbitrary manner in a constant non-uniform external magnetic field.
So, the excitation of the emf. induction when the circuit moves in a constant magnetic field is explained by the action of the magnetic component of the Lorentz force, proportional to 
, which occurs when the conductor moves. 
The experimentally observed occurrence of an induction current indicates that in this case, extraneous forces appear in the circuit, which are now associated with a time-varying magnetic field. What is their nature? The answer to this fundamental question was given by Maxwell.
Since the conductor is at rest, the speed of the ordered movement of electric charges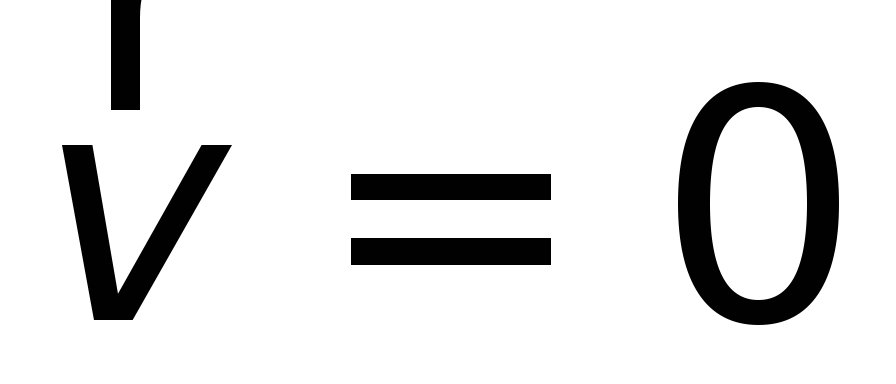 
and therefore a magnetic force proportional to 
, is also equal to zero and can no longer set charges in motion. However, in addition to the magnetic force, the only force that can act on an electric charge is the electric field, equal to 
. Therefore, it remains to conclude that induced current is caused by the electric field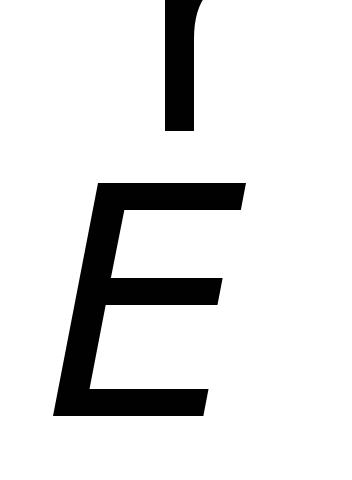 
, arising when the external magnetic field changes over time.
It is this electric field that is responsible for the appearance of emf. induction in a stationary circuit. According to Maxwell, a time-varying magnetic field generates an electric field in the surrounding space. The occurrence of an electric field is not associated with the presence of a conducting circuit, which only makes it possible to detect the existence of this field by the appearance of an induction current in it.
Formulation law of electromagnetic induction , given by Maxwell, is one of the most important generalizations of electrodynamics.
Any change in the magnetic field over time excites an electric field in the surrounding space .
The mathematical formulation of the law of electromagnetic induction in Maxwell’s understanding is:
Circulation of the tension vector 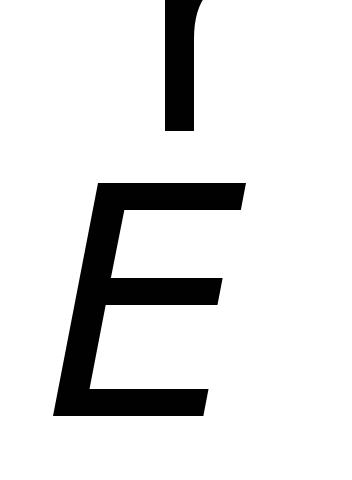of this field along any fixed closed contour 
is determined by the expression
|
|
Where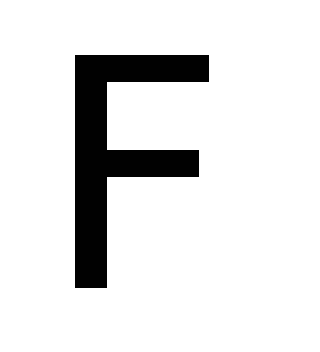 
- magnetic flux penetrating the circuit .
The partial derivative sign used to indicate the rate of change of magnetic flux indicates that the circuit is stationary.
Flow vector through a surface bounded by a contour , is equal 
, therefore, the expression of the law of electromagnetic induction can be rewritten as follows:
This is one of the equations in Maxwell's system of equations.
The fact that the circulation of the electric field excited by a time-varying magnetic field is nonzero means that the electric field in question not potential.It, like the magnetic field, is vortex.
In general, the electric field can be represented by the vector sum of the potential (field of static electric charges, the circulation of which is zero) and vortex (due to a time-varying magnetic field) electric fields.
At the basis of the phenomena we have considered, which explain the law of electromagnetic induction, there is no visible general principle that allows us to establish their commonality physical nature. Therefore, these phenomena should be considered as independent, and the law of electromagnetic induction - as the result of their joint action. All the more surprising is the fact that the emf. Induction in a circuit is always equal to the rate of change of magnetic flux through the circuit. In cases where the field also changes and the location or configuration of the circuit in the magnetic field, emf. induction should be calculated using the formula
The expression on the right side of this equality represents the total derivative of the magnetic flux with respect to time: the first term is associated with the change in the magnetic field over time, the second with the movement of the circuit.
We can say that in all cases the induced current is caused by the total Lorentz force
|
|
Which part of the induced current is caused by the electric and which magnetic component of the Lorentz force depends on choice of reference system.
On the work of the Lorentz and Ampere forces.
From the very definition of work it follows that a force acting in a magnetic field on an electric charge and perpendicular to its speed cannot do work. However, when a conductor with current moves, carrying charges along with it, the Ampere force still does work. Electric motors are a clear proof of this.
This contradiction disappears if we take into account that the movement of a conductor in a magnetic field is inevitably accompanied by the phenomenon of electromagnetic induction. Therefore, along with the Ampere force, work on electric charges The electromotive force of induction occurring in the conductor also performs. That., full time job The strength of the magnetic field consists of the mechanical work caused by the Ampere force and the work of the emf induced by the movement of the conductor. Both jobs are equal in magnitude and opposite in sign, so their sum is zero. Indeed, the work done by the ampere force during elementary movement of a conductor with current in a magnetic field is equal to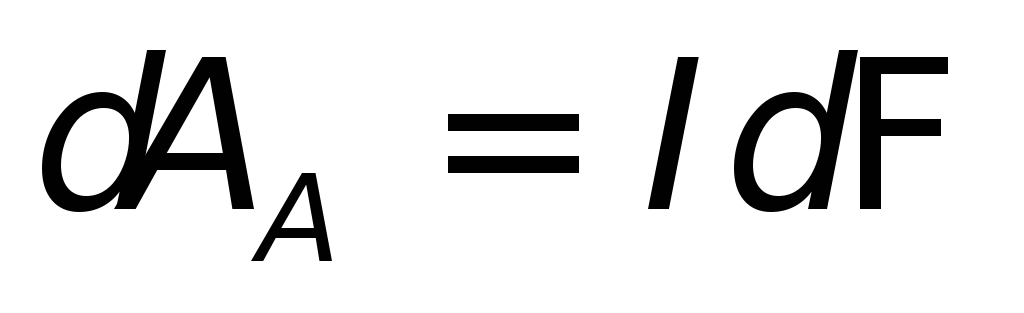 
, during the same time emf. induction does work
|
|
then full work 
.
Ampere forces do work not due to the energy of the external magnetic field, which can remain constant, but due to the emf source that maintains the current in the circuit.
As a result of numerous experiments, Faraday established the basic quantitative law of electromagnetic induction. He showed that whenever there is a change in the magnetic induction flux coupled to the circuit, an induced current appears in the circuit. The occurrence of an induction current indicates the presence in the circuit electromotive force, called electromotive force electromagnetic induction. Faraday established that the value of the emf of electromagnetic induction E i is proportional to the rate of change of the magnetic flux:
E i = -K, (27.1)
where K is a proportionality coefficient that depends only on the choice of units of measurement.
In the SI system of units, coefficient K = 1, i.e.
E i = - . (27.2)
This formula represents Faraday's law of electromagnetic induction. The minus sign in this formula corresponds to Lenz's rule (law).
Faraday's law can also be formulated in this way: the electromagnetic induction emf E i in a circuit is numerically equal and opposite in sign to the rate of change of the magnetic flux through the surface bounded by this circuit. This law is universal: EMF E i does not depend on the way the magnetic flux changes.
The minus sign in (27.2) shows that an increase in flux ( > 0) causes an emf E i< 0, т.е. магнитный поток индукционного тока направлен навстречу потоку, вызвавшему его; уменьшение потока ( < 0) вызывает E i >0 i.e. the directions of the magnetic flux of the induced current and the flux that caused it coincide. The minus sign in formula (27.2) is a mathematical expression of Lenz’s rule - general rule to find the direction of the induced current (and therefore the sign and emf of induction), derived in 1833. Lenz's rule: the induced current is always directed so as to counteract the cause that causes it. In other words, the induced current creates a magnetic flux that prevents the change in magnetic flux that causes the induced emf.
Induced emf is expressed in volts (V). Indeed, taking into account that the unit of magnetic flux is the weber (Wb), we obtain:
If the closed circuit in which the induced emf is induced consists of N turns, then E i will be equal to the sum of the emf induced in each of the turns. And if the magnetic flux covered by each turn is the same and equal to Ф, then the total flux through the surface of N turns is equal to (NF) - the total magnetic flux (flux linkage). In this case, the induced emf is:
E i = -N× , (27.3)
Formula (27.2) expresses the law of electromagnetic induction in general form. It applies to both stationary circuits and moving conductors in a magnetic field. The time derivative of the magnetic flux included in it generally consists of two parts, one of which is caused by the change in magnetic induction over time, and the other by the movement of the circuit relative to the magnetic field (or its deformation). Let's look at some examples of the application of this law.
Example 1. A straight conductor of length l moves parallel to itself in a uniform magnetic field (Figure 38). This conductor can be part of a closed circuit, the remaining parts of which are motionless. Let's find the emf arising in the conductor.
If the instantaneous value of the conductor speed is v, then in time dt it will describe the area dS = l× v×dt and during this time will cross all lines of magnetic induction passing through dS. Therefore, the change in magnetic flux through the circuit, which includes a moving conductor, will be dФ = B n ×l× v×dt. Here B n is the component of magnetic induction perpendicular to dS. Substituting this into formula (27.2) we get EMF value:
E i = B n ×l× v. (27.4)
The direction of the induced current and the sign of the EMF are determined by Lenz's rule: the induced current in the circuit always has such a direction that the magnetic field it creates prevents the change in the magnetic flux that caused this induced current. In some cases, it is possible to determine the direction of the induced current (the polarity of the induced emf) according to another formulation of Lenz’s rule: the induced current in a moving conductor is directed in such a way that the resulting Ampere force is opposite to the velocity vector (it slows down the movement).
Let's look at a numerical example. A vertical conductor (car antenna) with a length l = 2 m moves from east to west in the Earth’s magnetic field at a speed v= 72 km/h = 20 m/s. Let's calculate the voltage between the ends of the conductor. Since the conductor is open, there will be no current in it and the voltage at the ends will be equal to the induced emf. Considering that the horizontal component of the magnetic induction of the Earth's field (i.e. the component perpendicular to the direction of movement) for middle latitudes is equal to 2 × 10 -5 T, using formula (27.4) we find
U = Bn×l× v= 2×10 -5 ×2×20 = 0.8×10 -3 V,
those. about 1 mV. The Earth's magnetic field is directed from south to north. Therefore, we find that the emf is directed from top to bottom. This means that the lower end of the wire will have a higher potential (charged positively), and the upper end will have a lower potential (charged negatively).
Example 2. There is a closed wire circuit in a magnetic field, penetrated by a magnetic flux F. Let us assume that this flux decreases to zero and calculate the total amount of charge passed through the circuit. The instantaneous value of the emf during the disappearance of the magnetic flux is expressed by formula (27.2). Therefore, according to Ohm's law, the instantaneous value of the current is
where R is the total resistance of the circuit.
The amount of charge passed is equal to
q = = - = . (27.6)
The resulting relationship expresses the law of electromagnetic induction in the form found by Faraday, who from his experiments concluded that the amount of charge passed through the circuit is proportional to the total number of magnetic induction lines crossed by the conductor (i.e., the change in magnetic flux Ф 1 -Ф 2), and is inversely proportional to the resistance of the circuit R. Relationship (27.6) allows us to define the unit of magnetic flux in the SI system: weber - magnetic flux, when it decreases to zero, a charge of 1 C passes through a circuit coupled with it with a resistance of 1 Ohm.
According to Faraday's law, the occurrence of an electromagnetic induction emf is also possible in the case of a stationary circuit located in an alternating magnetic field. However, the Lorentz force is stationary charges doesn't work, so in this case it cannot be the cause of induced emf. To explain the induced emf in stationary conductors, Maxwell suggested that any alternating magnetic field excites a vortex electric field in the surrounding space, which is the cause of the appearance of induced current in the conductor. The circulation of the strength vector of this field along any fixed contour L of the conductor is the EMF of electromagnetic induction:
E i = = - . (27.7)
The vortex electric field strength lines are closed curves, therefore, when a charge moves in the vortex electric field non-zero work is done along a closed loop. This is the difference between a vortex electric field and an electrostatic field, the lines of intensity of which begin and end at the charges.
, and is determined only by the rate of its change, i.e. size 
.
,
.
,
.
,
