
>>Physics: Tension electric field. Principle of superposition of fields
It is not enough to say that an electric field exists. Must enter quantitative characteristic fields. After that, the electric fields can be compared with each other and continue to study their properties.
The electric field is detected by the forces acting on the charge. It can be argued that we know everything we need about the field if we know the force acting on any charge at any point in the field.
Therefore, it is necessary to introduce such a characteristic of the field, the knowledge of which will allow us to determine this force.
If we alternately place small charged bodies at the same point of the field and measure the forces, it will be found that the force acting on the charge from the field is directly proportional to this charge. Indeed, let the field be created by a point charge q 1. According to Coulomb's law (14.2) for a charge q2 there is a force proportional to the charge q2. Therefore, the ratio of the force acting on the charge placed at a given point of the field to this charge for each point of the field does not depend on the charge and can be considered as a characteristic of the field. This characteristic is called the electric field strength. Like a force, field strength - vector quantity; it is denoted by a letter. If the charge placed in the field is denoted by q instead of q2, then the stress will be:



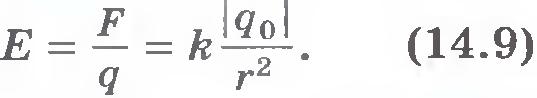

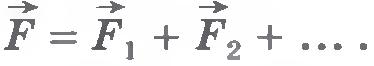
 etc., then the resulting field strength at this point is equal to the sum of the strengths of these fields:
etc., then the resulting field strength at this point is equal to the sum of the strengths of these fields:
moreover, the field strength created by a single charge is defined as if there were no other charges creating the field.
Thanks to the principle of superposition, to find the field strength of a system of charged particles at any point, it is enough to know the expression (14.9) for the field strength of a point charge. Figure 14.8 shows how the field strength at the point A, created by two point charges q 1 And q 2 , q 1 >q 2

???
1. What is called the strength of the electric field?
2. What is the field strength of a point charge?
3. How is the charge field strength q 0 directed if q0>0
? If q0<0
?
4. How is the principle of superposition of fields formulated?
G.Ya.Myakishev, B.B.Bukhovtsev, N.N.Sotsky, Physics Grade 10
Lesson content lesson summary support frame lesson presentation accelerative methods interactive technologies Practice tasks and exercises self-examination workshops, trainings, cases, quests homework discussion questions rhetorical questions from students Illustrations audio, video clips and multimedia photographs, pictures graphics, tables, schemes humor, anecdotes, jokes, comics parables, sayings, crossword puzzles, quotes Add-ons abstracts articles chips for inquisitive cheat sheets textbooks basic and additional glossary of terms other Improving textbooks and lessonscorrecting errors in the textbook updating a fragment in the textbook elements of innovation in the lesson replacing obsolete knowledge with new ones Only for teachers perfect lessons calendar plan for the year methodological recommendations of the discussion program Integrated LessonsIf you have corrections or suggestions for this lesson,
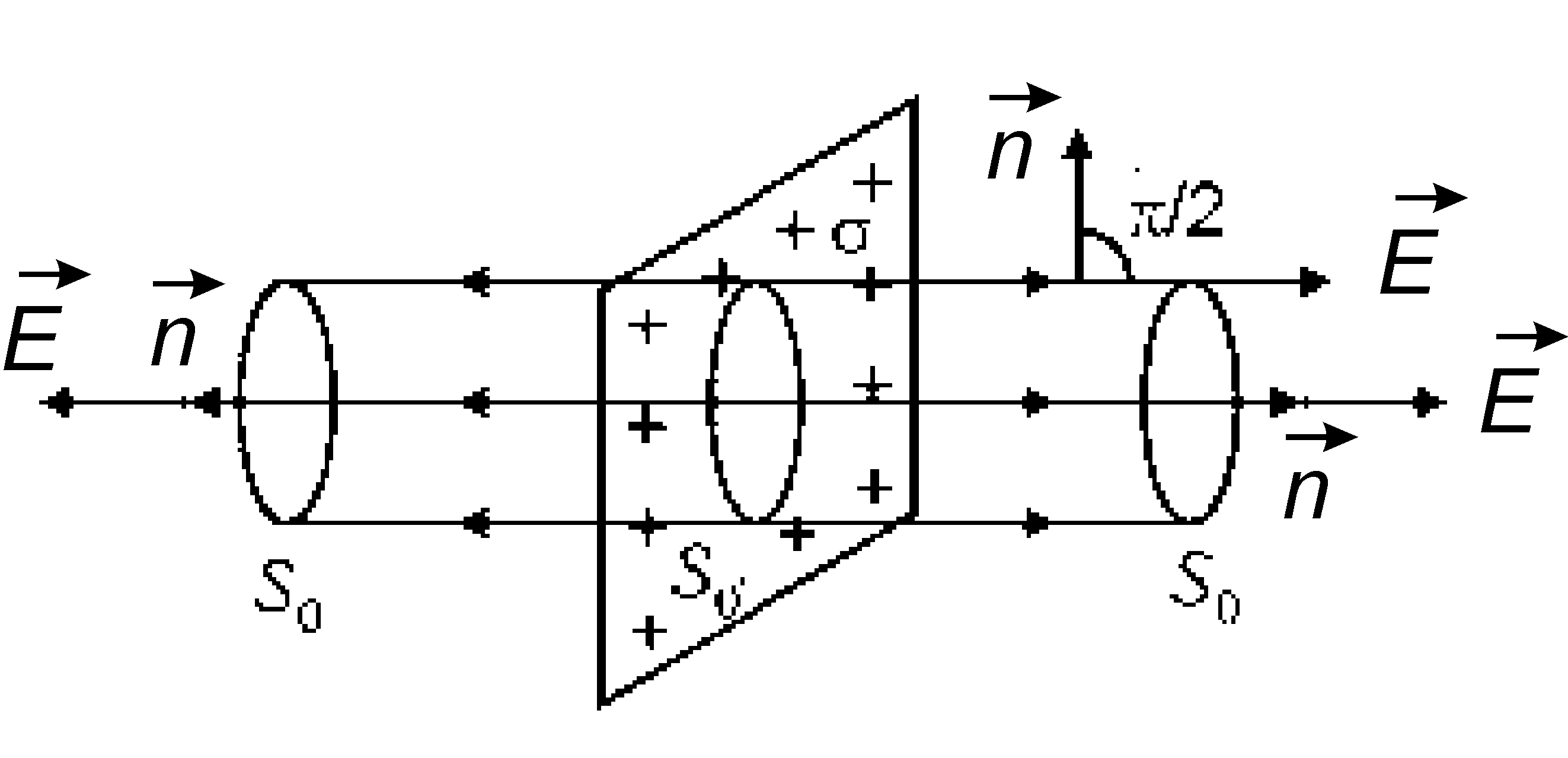
An infinite plane charged with a surface charge density: to calculate the electric field strength created by an infinite plane, we select a cylinder in space, the axis of which is perpendicular to the charged plane, and the bases are parallel to it and one of the bases passes through the field point of interest to us. According to the Gauss theorem, the flow of the electric field strength vector through a closed surface is:
Ф=, on the other hand it is: Ф=E
Equate the right parts of the equations:
We express = - through the surface charge density and find the electric field strength:
Find the electric field strength between oppositely charged plates with the same surface density:
Find the field outside the plates:
Field strength of a charged sphere
Ф= (2) t. Gauss
for r< R
; , because (there are no charges inside the sphere)
For r = R
( ; ; )
For r > R
The intensity of the field created by a ball charged uniformly throughout the volume
Volumetric charge density,
distributed over the ball:
For r< R
For r = R
For r > R
THE WORK OF THE ELECTROSTATIC FIELD ON THE MOVEMENT OF THE CHARGE
electrostatic field- email stationary charge field.
Fel, acting on the charge, moves it, doing work.
In a uniform electric field Fel = qE is a constant value
Field work (electronic force) does not depend on the shape of the trajectory and on a closed trajectory = zero.
| If in the electrostatic field of a point charge Q from point 1 to point 2 along any trajectory (Fig. 1) another point charge Q 0 moves, then the force applied to the charge does some work. The work of the force F on the elementary displacement dl is Since d l/cosα=dr, then Work when moving the charge Q 0 from point 1 to point 2 (1) does not depend on the trajectory of movement, but is determined only by the positions of the initial 1 and final 2 points. This means that the electrostatic field of a point charge is potential, and the electrostatic forces are conservative. From formula (1), it can be seen that the work that is done when an electric charge moves in an external electrostatic field along an arbitrary closed path L is equal to zero, i.e. (2) If we take a single point positive charge as a charge that is moved in an electrostatic field, then the elementary work of the field forces on the path dl is equal to Еdl = E l d l, where E l= Ecosα - the projection of the vector E on the direction of the elementary displacement. Then formula (2) can be represented as (3) The integral is called the circulation of the intensity vector. Hence, the circulation of the tension vector electrostatic field along any closed contour is equal to zero. A force field that has property (3) is called potential. From the zero circulation of the vector E it follows that the lines of the electrostatic field cannot be closed, they necessarily begin and end on charges (on positive or negative) or go to infinity. Formula (3) is valid only for an electrostatic field. In what follows, it will be shown that condition (3) is not true in the case of a field of moving charges (for it, the circulation of the intensity vector is nonzero). |
The circulation theorem for an electrostatic field.
Since the electrostatic field is central, the forces acting on a charge in such a field are conservative. Since it represents the elementary work that the field forces produce on a unit charge, the work of conservative forces on a closed loop is equal to
Potential
The "charge - electrostatic field" or "charge - charge" system has potential energy, just as the "gravitational field - body" system has potential energy.
The physical scalar quantity characterizing the energy state of the field is called potential given point in the field. A charge q is placed in the field, it has a potential energy W. Potential is a characteristic of an electrostatic field.
Consider potential energy in mechanics. Potential energy is zero when the body is on the ground. And when the body is raised to a certain height, then the body is said to have potential energy.
Regarding potential energy in electricity, there is no zero level potential energy. He is chosen at random. Therefore, the potential is a relative physical quantity.
The potential energy of a field is the work that an electrostatic force does when moving a charge from a given point in the field to a point with zero potential.
Let us consider a special case when an electrostatic field is created by an electric charge Q. To study the potential of such a field, there is no need to introduce a charge q into it. You can calculate the potential of any point of such a field, located at a distance r from the charge Q.
The dielectric constant of the medium has a known value (table), it characterizes the medium in which the field exists. For air, it is equal to one.
Potential difference
The work of the field to move the charge from one point to another is called the potential difference
This formula can be presented in a different form
Superposition principle
The potential of the field created by several charges is equal to the algebraic (taking into account the sign of the potential) sum of the potentials of the fields of each field separately
This is the energy of a system of fixed point charges, the energy of a solitary charged conductor and the energy of a charged capacitor.
If there is a system of two charged conductors (capacitor), then the total energy of the system is equal to the sum of the intrinsic potential energies of the conductors and the energy of their interaction:
Electrostatic field energy system of point charges is equal to:
A uniformly charged plane.
The electric field strength generated by an infinite plane charged with a surface charge density can be calculated using the Gauss theorem.
It follows from the symmetry conditions that the vector E everywhere perpendicular to the plane. In addition, at points symmetric with respect to the plane, the vector E will be the same in magnitude and opposite in direction.
As a closed surface, we choose a cylinder, the axis of which is perpendicular to the plane, and the bases are located symmetrically relative to the plane, as shown in the figure.
Since the lines of tension are parallel to the generators of the lateral surface of the cylinder, the flow through side surface equals zero. Therefore, the flow of the vector E through the surface of the cylinder
where is the area of the base of the cylinder. The cylinder cuts out the charge from the plane. If the plane is in a homogeneous isotropic medium with relative permittivity , then
When the field strength does not depend on the distance between the planes, such a field is called homogeneous. dependency graph E (x) for a plane.
Potential difference between two points located at distances R 1 and R 2 from the charged plane is equal to
Example 2. Two uniformly charged planes.
Let's calculate the strength of the electric field created by two infinite planes. The electric charge is distributed uniformly with surface densities and . We find the field strength as a superposition of the field strengths of each of the planes. The electric field is different from zero only in the space between the planes and is equal to .
Potential difference between the planes, where d- distance between planes.
The results obtained can be used for an approximate calculation of the fields created by flat plates of finite dimensions, if the distances between them are much less than their linear dimensions. Noticeable errors in such calculations appear when considering fields near the edges of the plates. dependency graph E (x) for two planes.
Example 3. A thin charged rod.
To calculate the strength of the electric field created by a very long rod charged with a linear charge density, we use the Gauss theorem.
Enough long distances from the ends of the rod, the electric field lines are directed radially from the axis of the rod and lie in planes perpendicular to this axis. At all points equidistant from the axis of the rod, the numerical values of the strength are the same if the rod is in a homogeneous isotropic medium with a relative dielectric
permeability.
To calculate the field strength at an arbitrary point located at a distance r from the axis of the rod, draw a cylindrical surface through this point
(see picture). The radius of this cylinder is r, and its height h.
The fluxes of the tension vector through the upper and lower bases of the cylinder will be equal to zero, since the lines of force do not have components normal to the surfaces of these bases. At all points on the lateral surface of the cylinder
E= const.
Therefore, the total flow of the vector E through the surface of the cylinder will be equal to
By the Gauss theorem, the flow of the vector E is equal to the algebraic sum of electric charges located inside the surface (in this case cylinder) divided by the product of the electrical constant and the relative permittivity of the medium
where is the charge of that part of the rod that is inside the cylinder. Therefore, the electric field strength
The potential difference of the electric field between two points located at distances R 1 and R 2 from the axis of the rod, we will find using the relationship between the strength and potential of the electric field. Since the field strength changes only in the radial direction, then
Example 4. Charged spherical surface.
The electric field created by a spherical surface, over which an electric charge with a surface density is uniformly distributed, has a centrally symmetric character.
The lines of tension are directed along the radii from the center of the sphere, and the modulus of the vector E only depends on the distance r from the center of the sphere. To calculate the field, we choose a closed spherical surface of radius r.
When r o
The field strength is zero, since there is no charge inside the sphere.
For r > R (outside the sphere), according to the Gauss theorem
where is the relative permittivity of the medium surrounding the sphere.
The intensity decreases according to the same law as the field strength of a point charge, i.e., according to the law.
When r o
dependency graph E (r) for the sphere.
Example 5. Volume-charged dielectric ball.
If a ball with a radius R from a homogeneous isotropic dielectric with a relative permittivity is uniformly charged over the volume with a density electric field is also centrally symmetrical.
As in the previous case, we choose a closed surface to calculate the vector flow E in the form of a concentric sphere, the radius of which r can vary from 0 to .
At r < R flow vector E through this surface will be determined by the charge
So
At r < R(inside the ball).
Inside the ball, the tension increases in direct proportion to the distance from the center of the ball. Outside the ball (at r > R) in a medium with permittivity , the flux vector E across the surface will be determined by the charge.
When r o >R o (outside the ball) .
On the border of the "ball - environment"The electric field strength changes abruptly, the value of which depends on the ratio of the dielectric constants of the ball and the medium. Dependence graph E (r) for ball().
Outside the ball ( r > R) the potential of the electric field varies according to the law
.
inside the ball ( r < R) the potential is described by the expression
In conclusion, we give expressions for calculating the field strengths of charged bodies of various shapes
| Potential difference | |
| Voltage- the difference between the values of the potential at the initial and final points of the trajectory. Voltage numerically equal to the work of the electrostatic field when moving a unit positive charge along the lines of force of this field. Potential difference (voltage) does not depend on the choice coordinate systems! | |
| The unit of potential difference The voltage is 1 V if, when a positive charge of 1 C moves along the lines of force, the field does work of 1 J. |
Conductor- This solid, in which there are “free electrons” moving within the body.
Metal conductors are generally neutral: they have an equal number of negative and positive charges. Positively charged are ions in the nodes of the crystal lattice, negative are electrons that freely move along the conductor. When a conductor is given an excess number of electrons, it becomes negatively charged, but if a certain amount of electrons is “taken away” from the conductor, it becomes positively charged.
The excess charge is distributed only over outer surface conductor.
1 . The field strength at any point inside the conductor is zero.
2 . The vector on the surface of the conductor is directed along the normal to each point on the surface of the conductor.
From the fact that the surface of the conductor is equipotential, it follows that directly at this surface the field is directed along the normal to it at each point (the condition 2 ). If this were not the case, then under the action of the tangential component, the charges would move along the surface of the conductor. those. equilibrium of charges on a conductor would be impossible.
From 1 it follows that since
There are no excess charges inside the conductor.
Charges are distributed only on the surface of the conductor with a certain density s and are located in a very thin surface layer (its thickness is about one or two interatomic distances).
charge density- this is the amount of charge per unit length, area or volume, thus determining the linear, surface and volume charge densities, which are measured in the SI system: in Coulombs per meter [C/m], in Coulombs per square meter[C/m²] and in Coulomb per cubic meter[C/m³], respectively. Unlike the density of matter, the charge density can have both positive and negative values, this is due to the fact that there are positive and negative charges.
General task electrostatics
tension vector,
according to the Gauss theorem
Poisson equation.
In the case - there are no charges between the conductors, we get
- Laplace equation.
Let the boundary conditions on the surfaces of conductors be known: values ; then this problem has a unique solution according to uniqueness theorem.
When solving the problem, the value is determined and then the field between the conductors is determined by the distribution of charges on the conductors (according to the intensity vector near the surface).
Consider an example. Find the tension in the empty cavity of the conductor.
The potential in the cavity satisfies the Laplace equation;
potential on the walls of the conductor.
The solution of the Laplace equation in this case is trivial, and by the uniqueness theorem there are no other solutions
, i.e. there is no field in the conductor cavity.
Poisson equation- elliptical differential equation in partial derivatives, which, among other things, describes
the electrostatic field
stationary temperature field,
The pressure field
· velocity potential field in hydrodynamics.
It is named after the famous French physicist and mathematician Simeon Denis Poisson.
This equation looks like:
where is the Laplace operator or Laplacian, and is a real or complex function on some manifold.
In a three-dimensional Cartesian coordinate system, the equation takes the form:
In the Cartesian coordinate system, the Laplace operator is written in the form and the Poisson equation takes the form:
If f tends to zero, then the Poisson equation turns into the Laplace equation (the Laplace equation is a special case of the Poisson equation):
Poisson's equation can be solved using the Green's function; see, for example, the article screened Poisson equation. Eat various methods to obtain numerical solutions. For example, an iterative algorithm is used - the "relaxation method".
| We will consider a solitary conductor, i.e., a conductor significantly removed from other conductors, bodies and charges. Its potential, as you know, is directly proportional to the charge of the conductor. It is known from experience that different conductors, being equally charged, have different potentials. Therefore, for a solitary conductor, you can write the Value (1) is called the electrical capacity (or simply capacitance) of a solitary conductor. The capacitance of a solitary conductor is given by a charge, the communication of which to the conductor changes its potential by one. The capacitance of a solitary conductor depends on its size and shape, but does not depend on the material, shape and size of the cavities inside the conductor, as well as its state of aggregation. The reason for this is that excess charges are distributed on the outer surface of the conductor. The capacitance also does not depend on the charge of the conductor, nor on its potential. The unit of electrical capacity is farad (F): 1 F is the capacitance of such a solitary conductor, in which the potential changes by 1 V when a charge of 1 C is imparted to it. According to the formula for the potential of a point charge, the potential of a solitary ball of radius R, which is located in a homogeneous medium with a permittivity ε, is equal to Applying formula (1), we obtain that the capacitance of the ball (2) From this it follows that a solitary ball would have a capacity of 1 F, located in a vacuum and having a radius R=C/(4πε 0)≈9 10 6 km, which is approximately 1400 times greater than the radius of the Earth (electric capacity of the Earth C≈0.7 mF). Consequently, the farad is a rather large value, therefore, in practice, submultiple units are used - millifarad (mF), microfarad (μF), nanofarad (nF), picofarad (pF). It also follows from formula (2) that the unit of the electrical constant ε 0 is a farad per meter (F/m) (see (78.3)). |
Capacitor(from lat. condensare- “compact”, “thicken”) - a two-terminal network with a certain value of capacitance and low ohmic conductivity; a device for accumulating charge and energy of an electric field. The capacitor is a passive electronic component. Usually consists of two plate-shaped electrodes (called facings), separated by a dielectric, the thickness of which is small compared to the dimensions of the plates.
Capacity
The main characteristic of a capacitor is its capacity characterizing the ability of a capacitor to store an electric charge. The value of the nominal capacity appears in the designation of the capacitor, while the actual capacity can vary significantly depending on many factors. The actual capacitance of a capacitor determines its electrical properties. So, by definition of capacitance, the charge on the plate is proportional to the voltage between the plates ( q=CU). Typical capacitance values range from picofarads to thousands of microfarads. However, there are capacitors (ionistors) with a capacity of up to tens of farads.
Capacitance of a flat capacitor, consisting of two parallel metal plates with an area S each located at a distance d from each other, in the SI system is expressed by the formula: This formula is valid only when d much smaller than the linear dimensions of the plates.
To obtain large capacitances, capacitors are connected in parallel. In this case, the voltage between the plates of all capacitors is the same. Total battery capacity parallel connected capacitors is equal to the sum of the capacitances of all capacitors included in the battery.
If all capacitors connected in parallel have the same distance between the plates and the properties of the dielectric, then these capacitors can be represented as one large capacitor, divided into fragments of a smaller area.
When capacitors are connected in series, the charges of all capacitors are the same, since they are supplied from the power source only to the external electrodes, and on the internal electrodes they are obtained only due to the separation of charges that previously neutralized each other. Total battery capacity successively connected capacitors is
This capacitance is always less than the minimum capacitance of the capacitor included in the battery. However, when connected in series, the possibility of breakdown of capacitors is reduced, since each capacitor accounts for only a part of the potential difference of the voltage source.
If the area of the plates of all capacitors connected in series is the same, then these capacitors can be represented as one large capacitor, between the plates of which there is a stack of dielectric plates of all the capacitors that make it up.
[edit] Specific capacity
Capacitors are also characterized by specific capacitance - the ratio of capacitance to the volume (or mass) of the dielectric. The maximum specific capacitance value is reached at minimum thickness dielectric, but this reduces its breakdown voltage.
IN electrical circuits various ways to connect capacitors. Connection of capacitors can be made: successively, parallel And series-parallel(the latter is sometimes called a mixed capacitor connection). Existing species capacitor connections are shown in figure 1.
Figure 1. Methods for connecting capacitors.
Lecture 19.
The force of interaction between two point fixed charges is determined by Coulomb's law: two point charges stationary charge interact with each other with a force proportional to the product of the charges and inversely proportional to the square of the distance between them:
| , | (1.1) |
 , where 0 - SI electric constant, 0 =
8.85 10 -12 C 2 / (N m 2).
, where 0 - SI electric constant, 0 =
8.85 10 -12 C 2 / (N m 2). Thus, for charges located in vacuum, Coulomb's law has the form
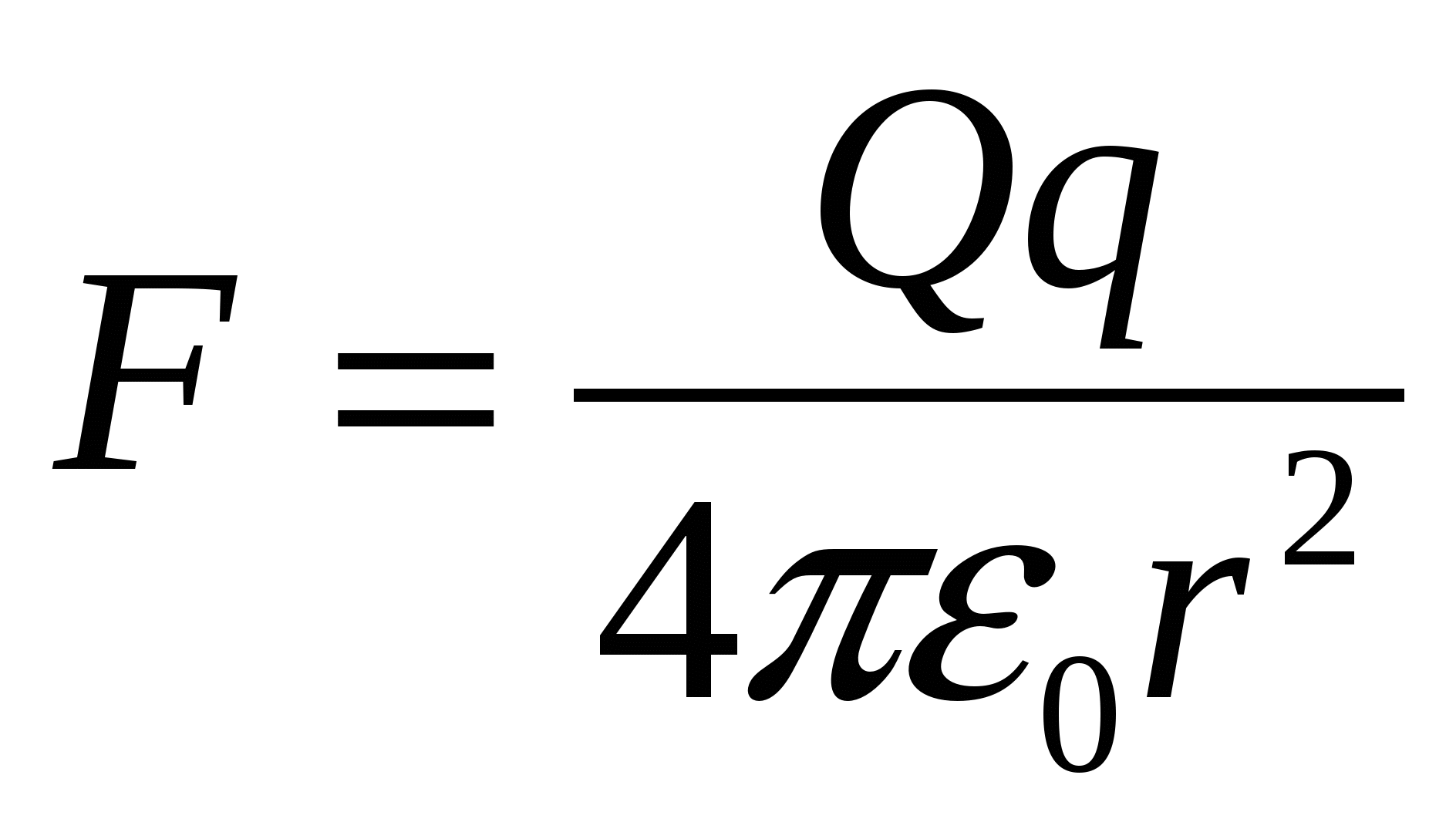 . .
| (1.2) |
The power characteristic of the electric field is the intensity 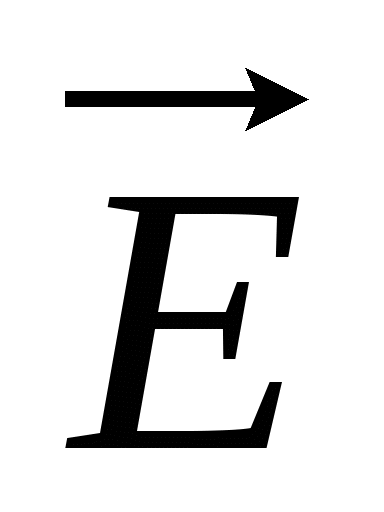 - a vector quantity, the module of which is equal to the force acting from the electrostatic field on a unit charge; and the direction is the same as the direction of the force acting on the positive charge
- a vector quantity, the module of which is equal to the force acting from the electrostatic field on a unit charge; and the direction is the same as the direction of the force acting on the positive charge
Where EWith is the strength of the electrostatic field in the medium.
If the electrostatic field is created by several charges, then, in accordance with the principle of superposition, the total field strength at a certain point is defined as the vector sum of the strengths created at this point by individual charges:
  | (1.5) |
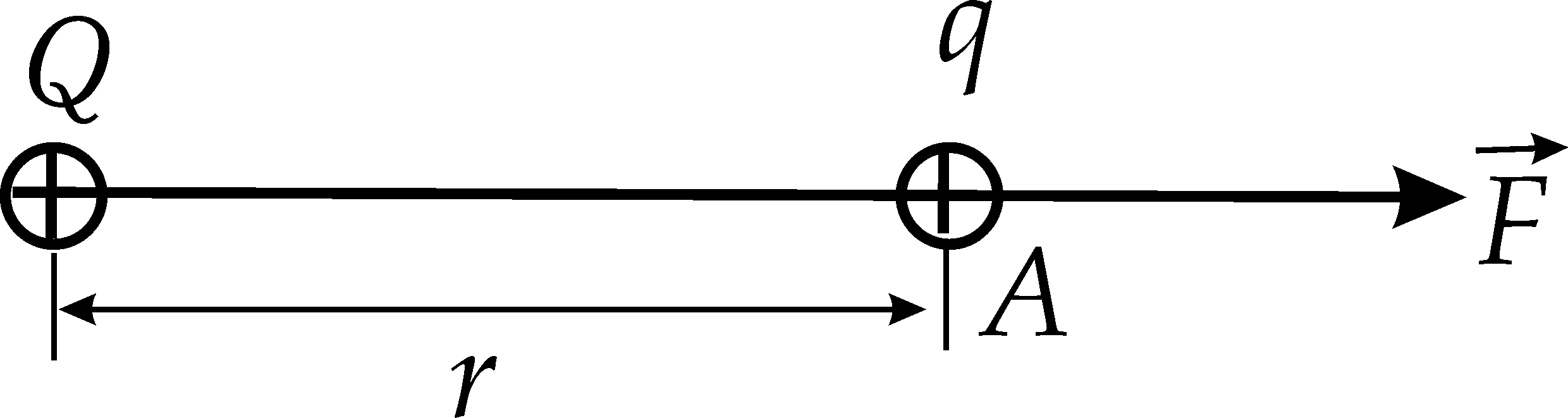
Rice. 1.1
 | (1.8) |
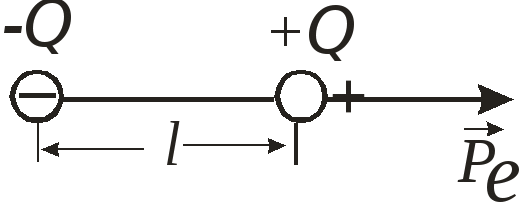
Rice. 1.2
dipole moment (electric moment of the dipole). The dipole moment is directed along the dipole axis towards the positive charge (Fig. 1.2). Let us now find the dipole field strength, restricting ourselves to the case r>>l.
^
A. Field strength at a point located on the continuation of the dipole axis
In accordance with the principle of superposition, the field strength at the point A(Fig. 1.3)

Rice. 1.3
Where  And
And  is the strength of the field created by the charges, respectively +Q
And -Q.
Since the vectors
And
directed in opposite directions, then the modulus of the vector
will
is the strength of the field created by the charges, respectively +Q
And -Q.
Since the vectors
And
directed in opposite directions, then the modulus of the vector
will  , where in accordance with (1.6)
, where in accordance with (1.6) 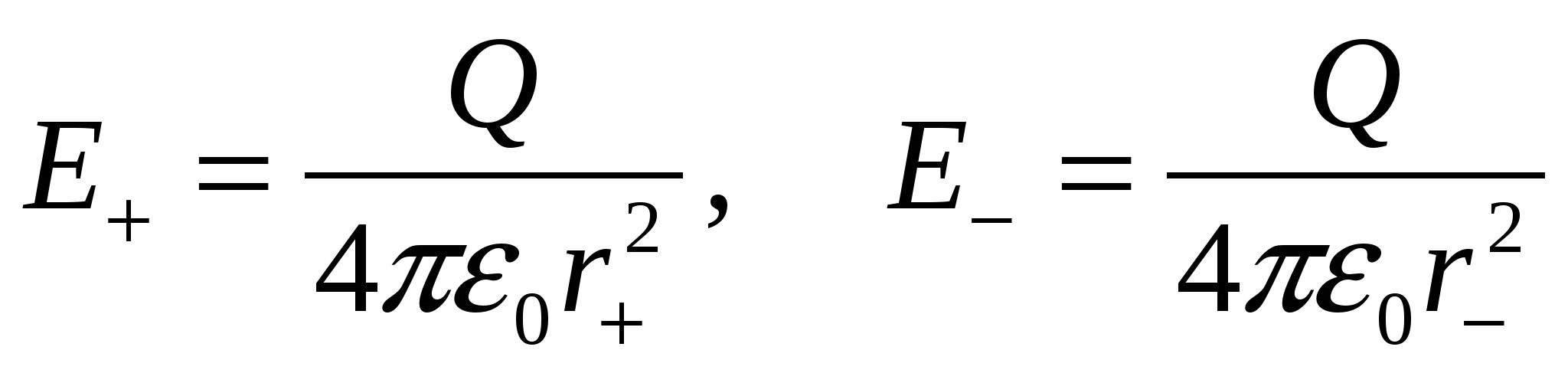 . Thus,
. Thus,  .
.
We transform the expression in brackets as follows. From fig. 1.3 shows that 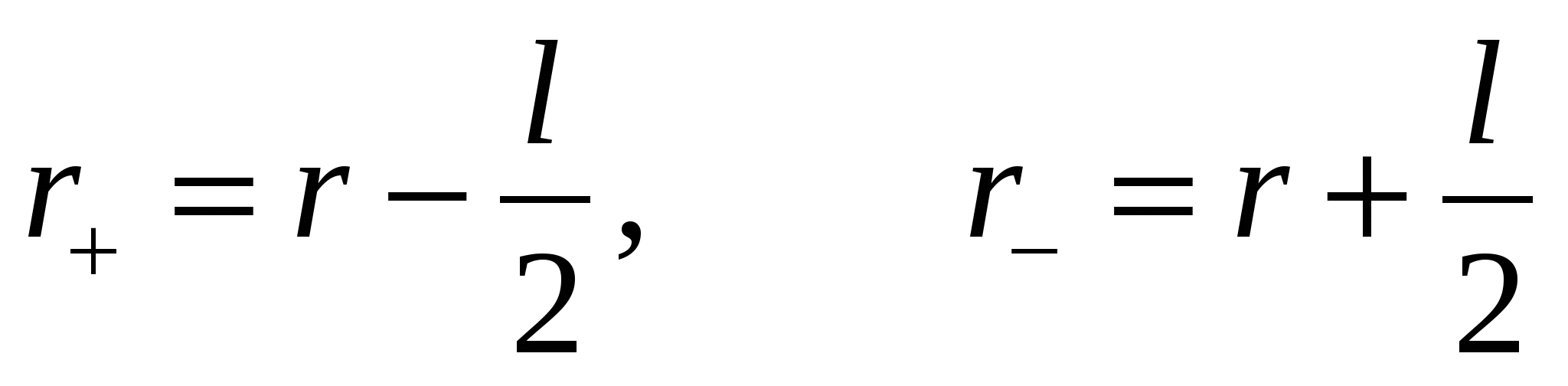 , Where r is the distance between the point A and the center of the dipole. Then we have
, Where r is the distance between the point A and the center of the dipole. Then we have
 .
.
Because the r>>l,
then the value 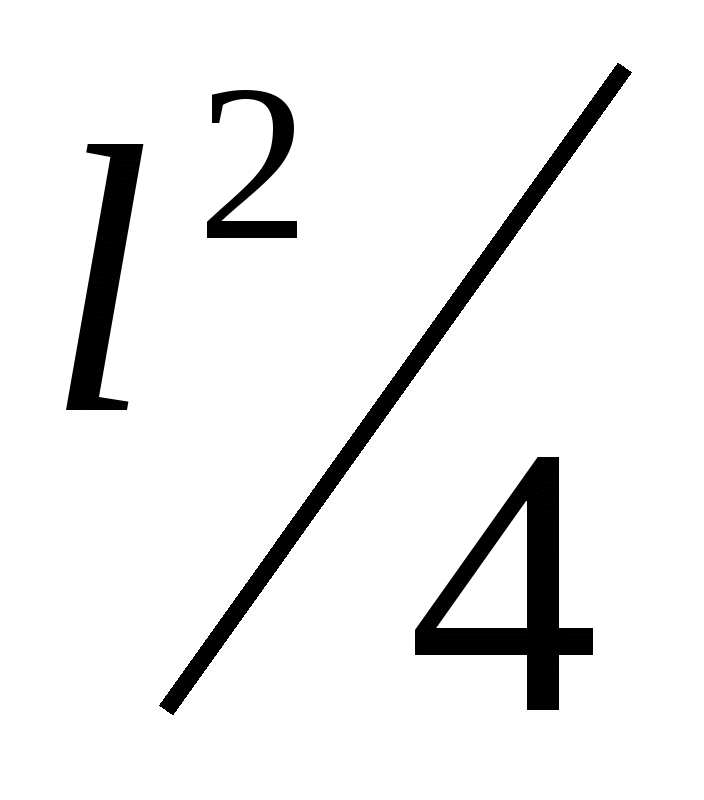 can be neglected in the denominator, so
can be neglected in the denominator, so  ;
;
 . Because Ql is a dipole moment, then
. Because Ql is a dipole moment, then 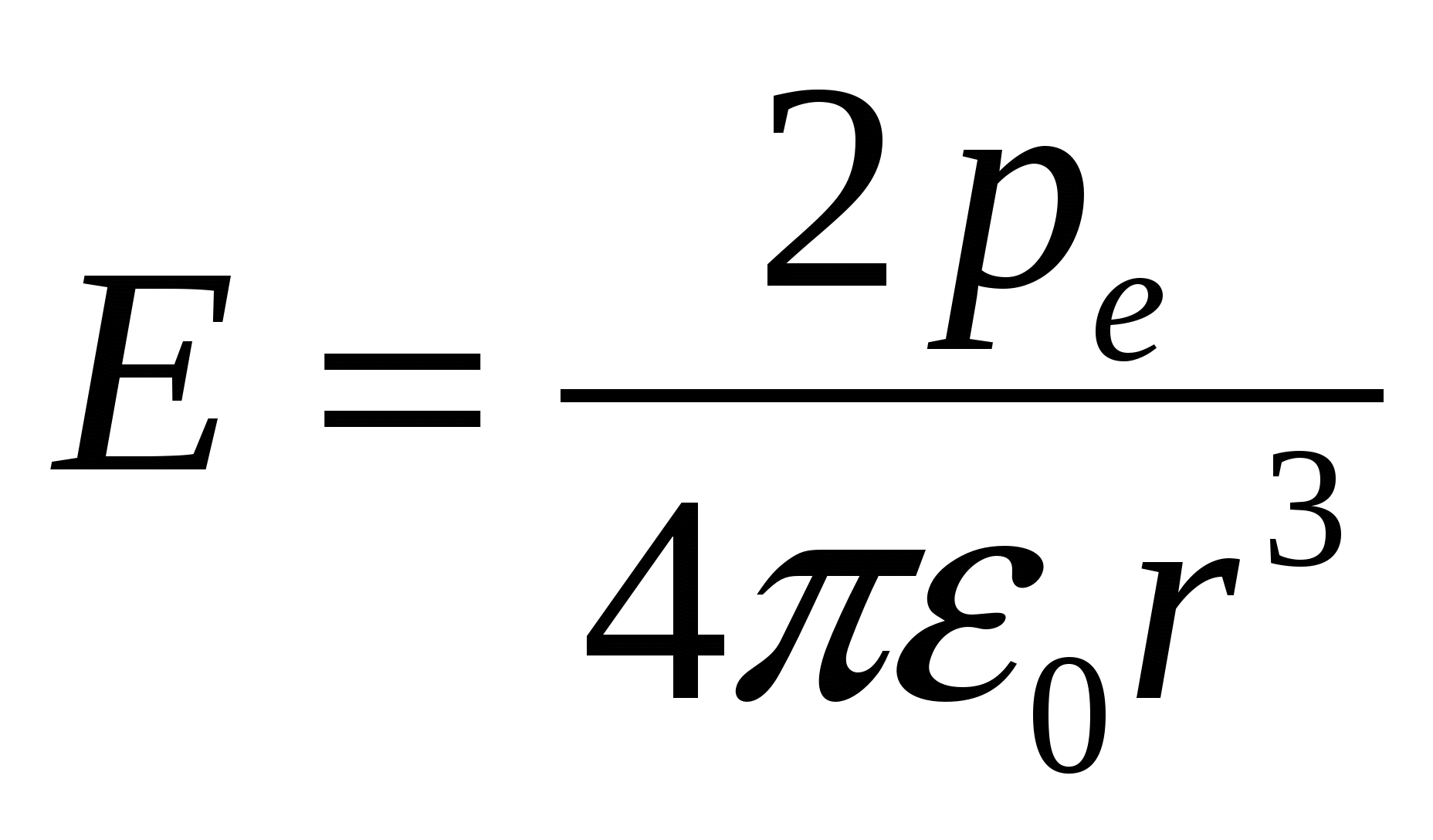
B. Field strength at the perpendicular to the dipole axis

Rice. 1.4
From fig. 1.4 shows that 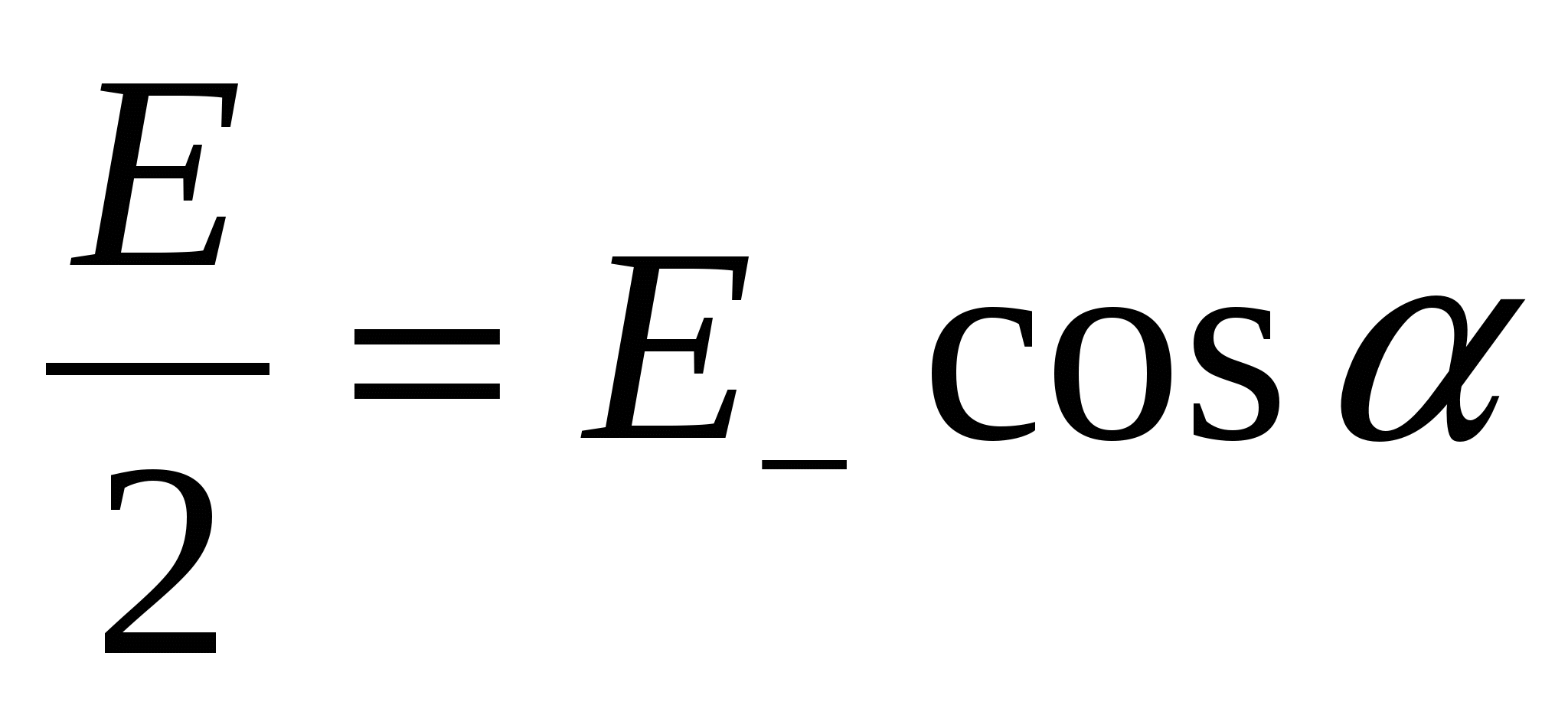 .Further
.Further 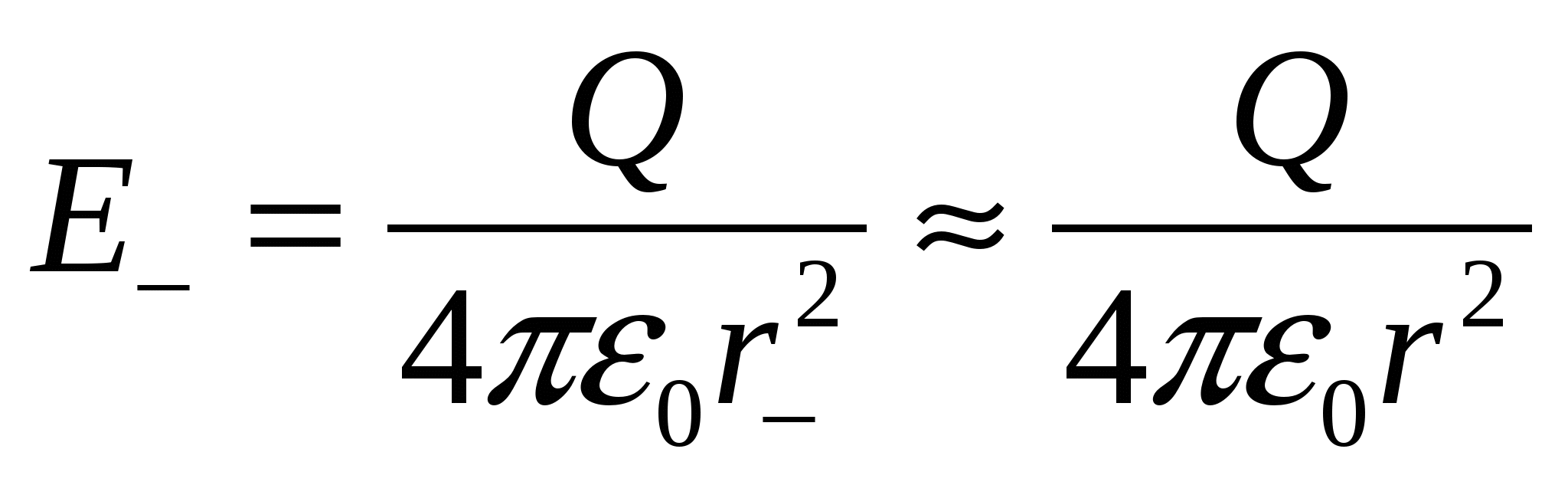 ,
,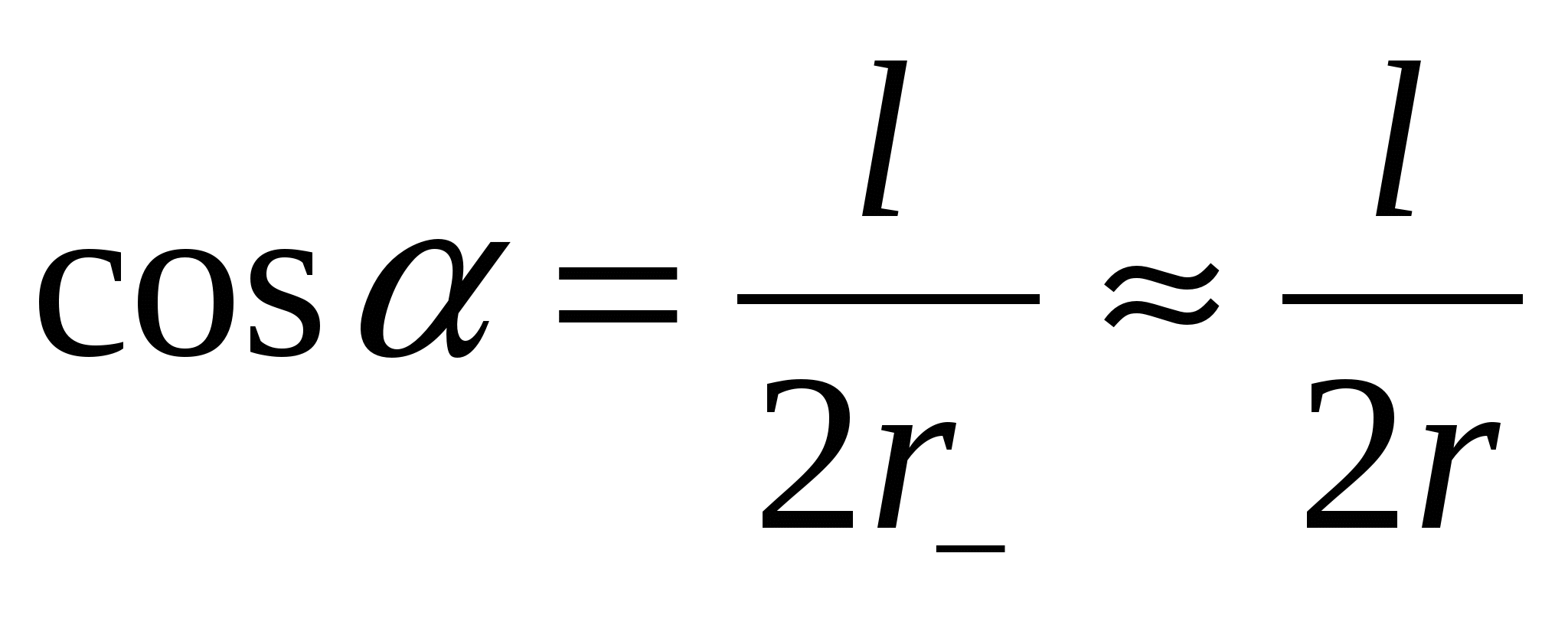 ,
,
Hence,  , Where Pl=Ql is the dipole moment. Thus,
, Where Pl=Ql is the dipole moment. Thus,
 . .
| (1.10) |
 (Fig. 1.5).
(Fig. 1.5). 
Rice. 1.5
Field line properties:
a) the lines of force of the electrostatic field do not intersect;
b) the lines of force of the electrostatic field are open - they start on positive charges and end on negative ones (or go to infinity).
Let us introduce the concept of the flow of the field strength vector . By definition, the elementary flux of the intensity vector through the site dS
Where  is a unit vector coinciding with the normal.
is a unit vector coinciding with the normal.
The total flow of the intensity vector through any surface can be found by integrating (11.12) for the entire surface  for a closed surface
for a closed surface 
The most important role in electrostatics is played by the Ostrogradsky-Gauss theorem, which is formulated as follows: the flux of the intensity vector through any closed surface is proportional to the algebraic sum of the charges inside this surface:
 , (1.13)
, (1.13)

Rice. 1.6
Proof. Let us consider the simplest case, when a closed surface is a sphere, in the center of which there is a point charge +Q(Fig. 1.7). We single out an elementary area on the sphere dS. Normal to this site and vector coincide in direction, so .
![]()
Rice. 1.7
We transform the integrand in (1.13) as follows:
Taking into account that everywhere on the surface of the sphere E= const, and taking into account the expression (11.6), we get:
The theorem has been proved for the particular case when there is one charge inside the spherical surface. The proof is easily generalized to the case of an arbitrary number of charges and an arbitrary closed surface.
In the total flow, which is created by charges located outside the closed surface, positive and negative parts can be distinguished, which are mutually compensated. Therefore, the charges external to the given closed surface are not taken into account in the Ostrogradsky-Gauss theorem.
The Ostrogradsky-Gauss theorem connects charges with the electric fields they create and reflects the fact that stationary electric charges serve as the source of an electrostatic field.
This theorem is closely related to Coulomb's law: if Coulomb's law is valid, then the Ostrogradsky-Gauss theorem is also valid, and vice versa. If in Coulomb's law the exponent was at least slightly different from two, i.e. F
1/ r 2+
α
, Where α
–
arbitrarily small number, then the Ostrogradsky-Gauss theorem would be violated. The validity of the Ostrogradsky-Gauss theorem has been experimentally verified with much greater accuracy than the Coulomb law.
^
1.5. Application of the Ostrogradsky-Gauss theorem to calculate fields
The Ostrogradsky-Gauss theorem in some cases makes it relatively easy to calculate the strength of the electrostatic field for a given charge distribution. Let's look at a few examples.
^
1.5.1. Field of an infinite uniformly charged plane
Let there be an infinite uniformly charged plane with a surface charge density
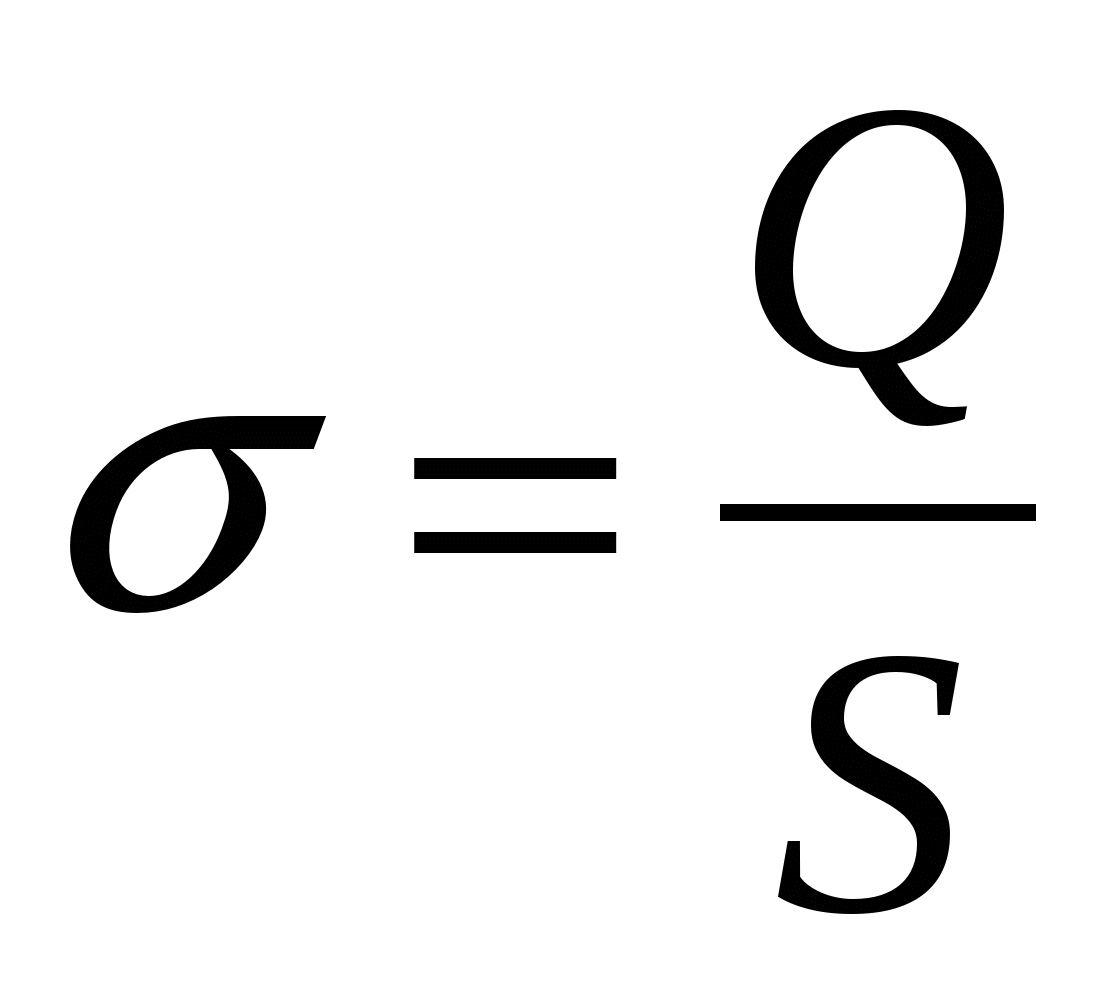 [C/m 2
]
[C/m 2
]
From symmetry considerations it follows that the vector must be perpendicular to the plane. Let's choose a closed surface in the form of a cylinder, the lateral surface of which is oriented along the vector (Fig. 11.8). Total vector flow
, obviously, is
Rice. 1.8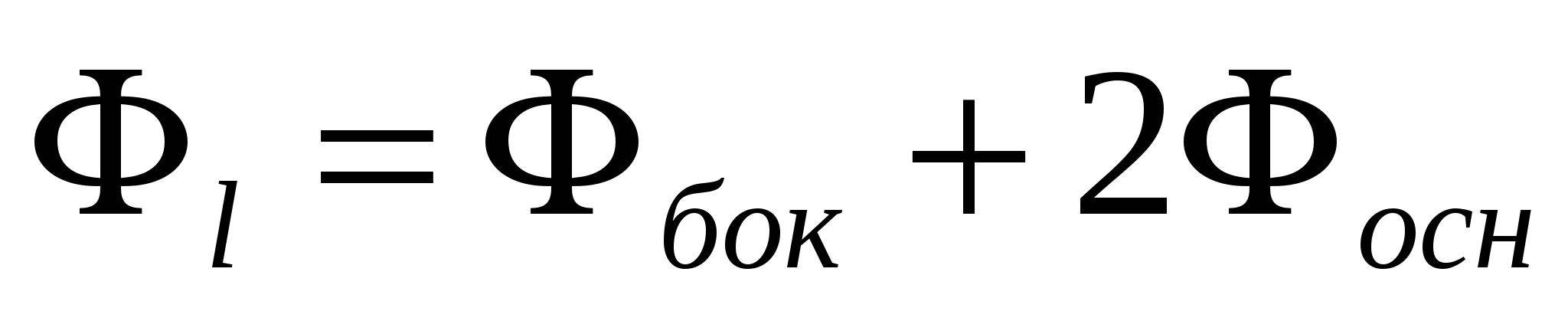 .
.
The flow through the side surface is zero, since (Fig. 1.8):
Flow through cylinder base:
 .
.
So the total flow of the vector E through a closed surface  .
.
According to the Ostrogradsky-Gauss theorem 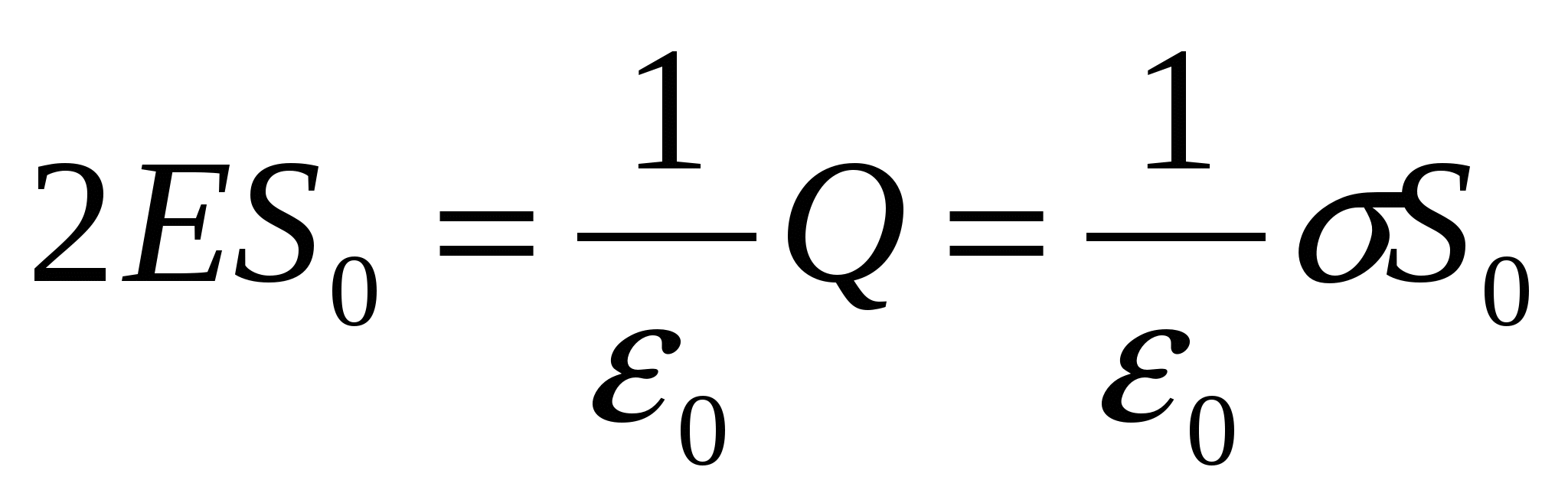 . Hence the field strength
. Hence the field strength
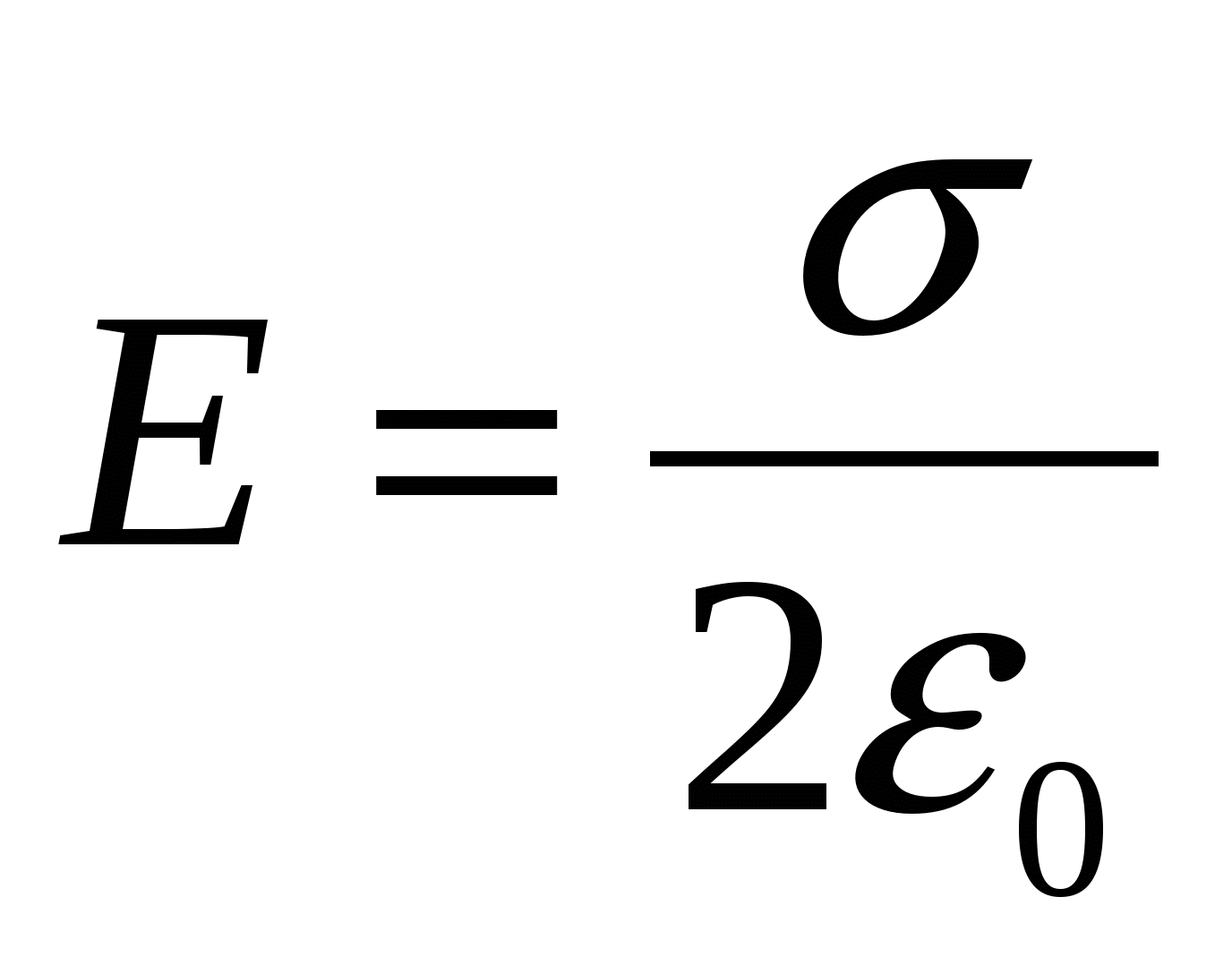 , (1.14)
, (1.14)
The intensity of the field created by an infinite uniformly charged plane does not depend on the distance to it. A field in which the intensity vector is the same in magnitude and direction is called homogeneous.
^
11.5.2. Field of two infinite uniformly charged planes
Let us calculate the strength of the field created by two infinite parallel planes, uniformly charged with a surface charge density of +σ and -σ (Fig. 11.9).
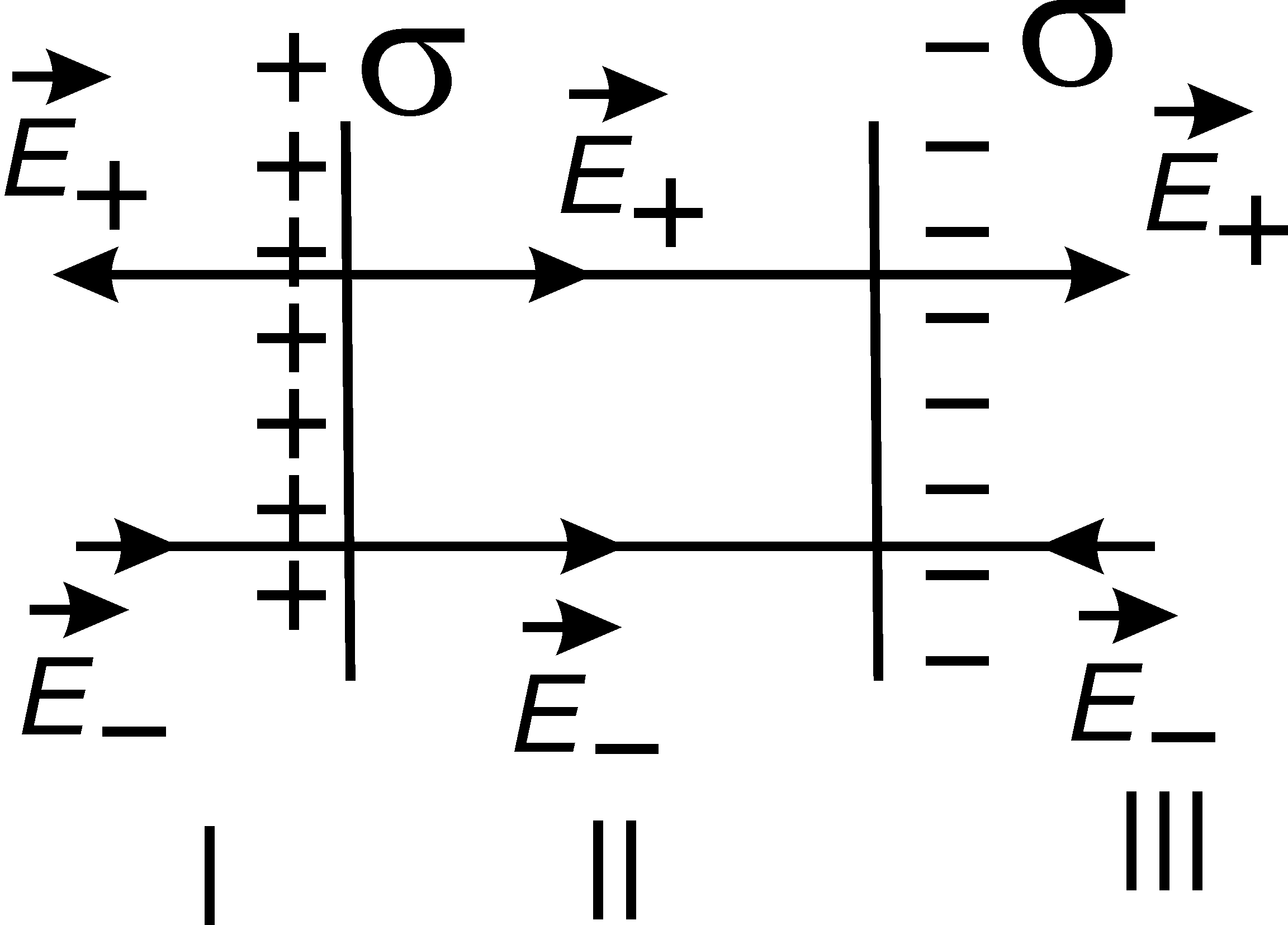
Rice. 1.9
According to the superposition principle, the total field strength
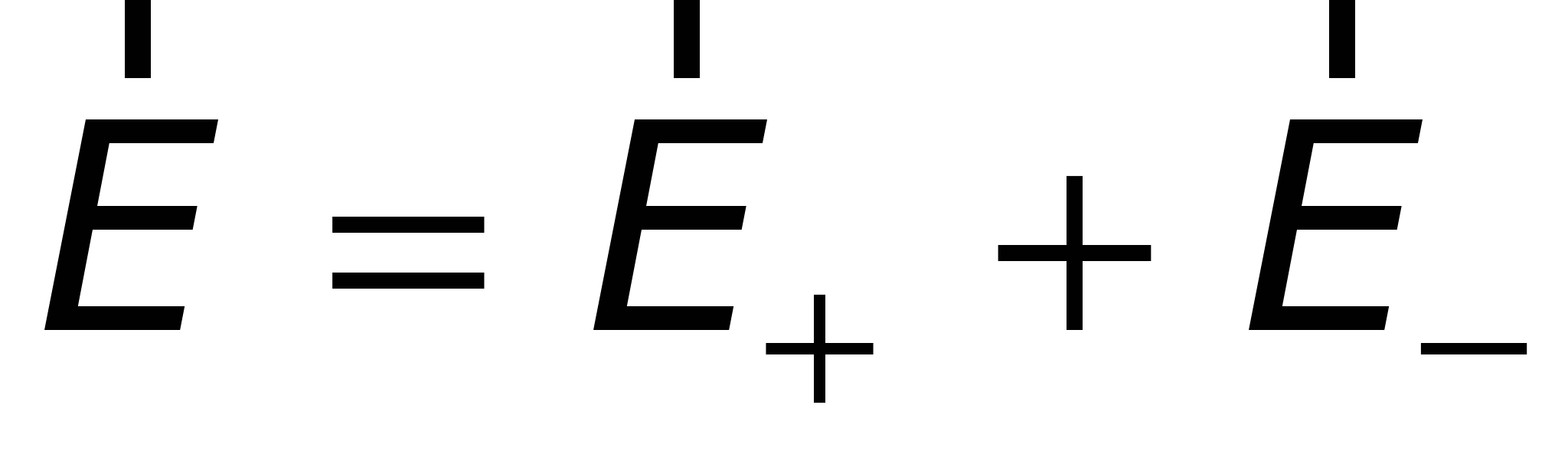 ,
,
Where 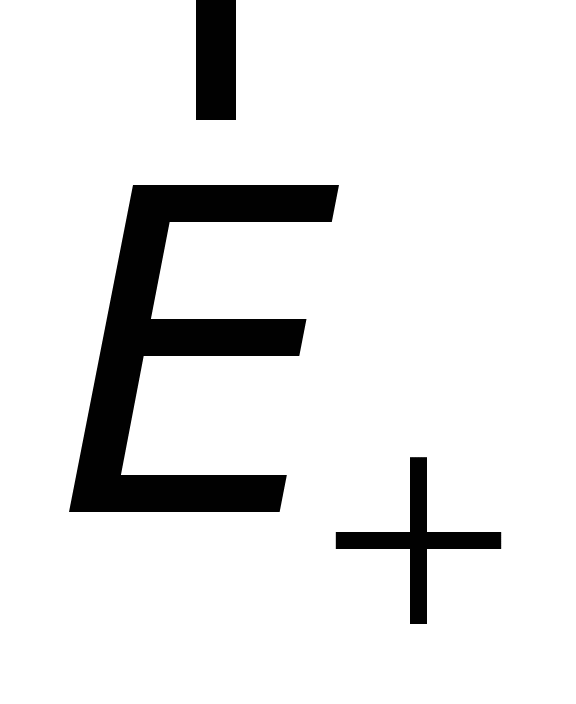 And
And 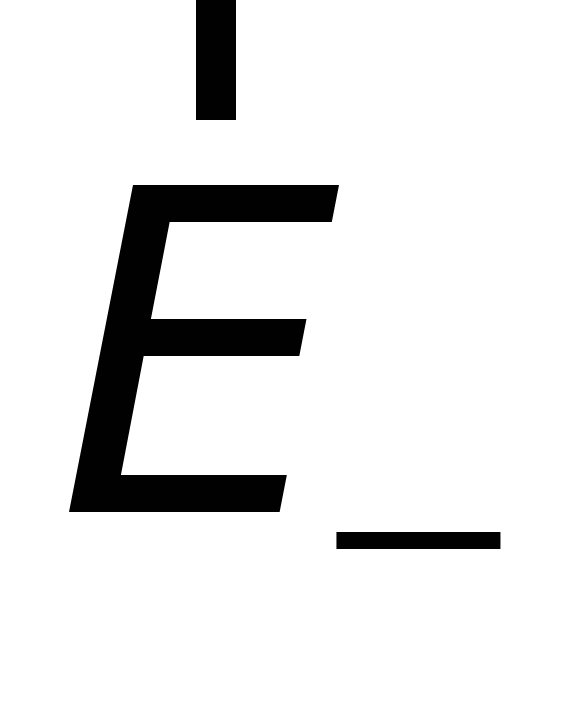 is the strength of the field generated by the positively and negatively charged planes, respectively.
is the strength of the field generated by the positively and negatively charged planes, respectively.
In areas of space I and III (Fig. 1.9), the vectors and are directed in opposite directions, so the total tension 
In region II, and are parallel and equal in absolute value, therefore 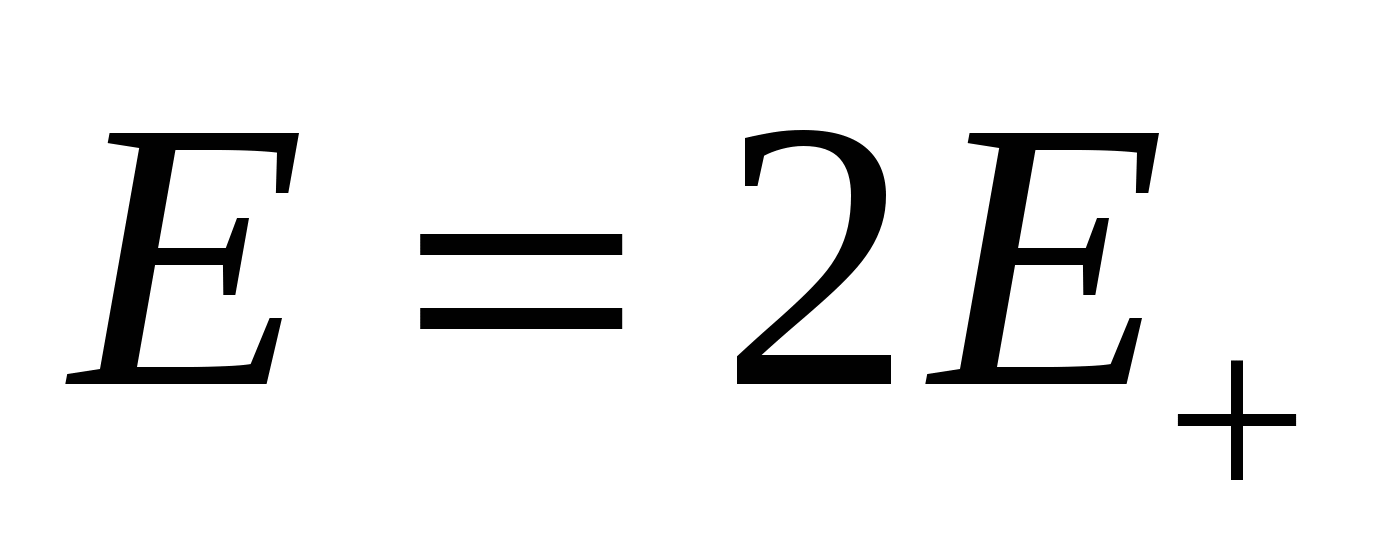 . Using the previous result, we get
. Using the previous result, we get 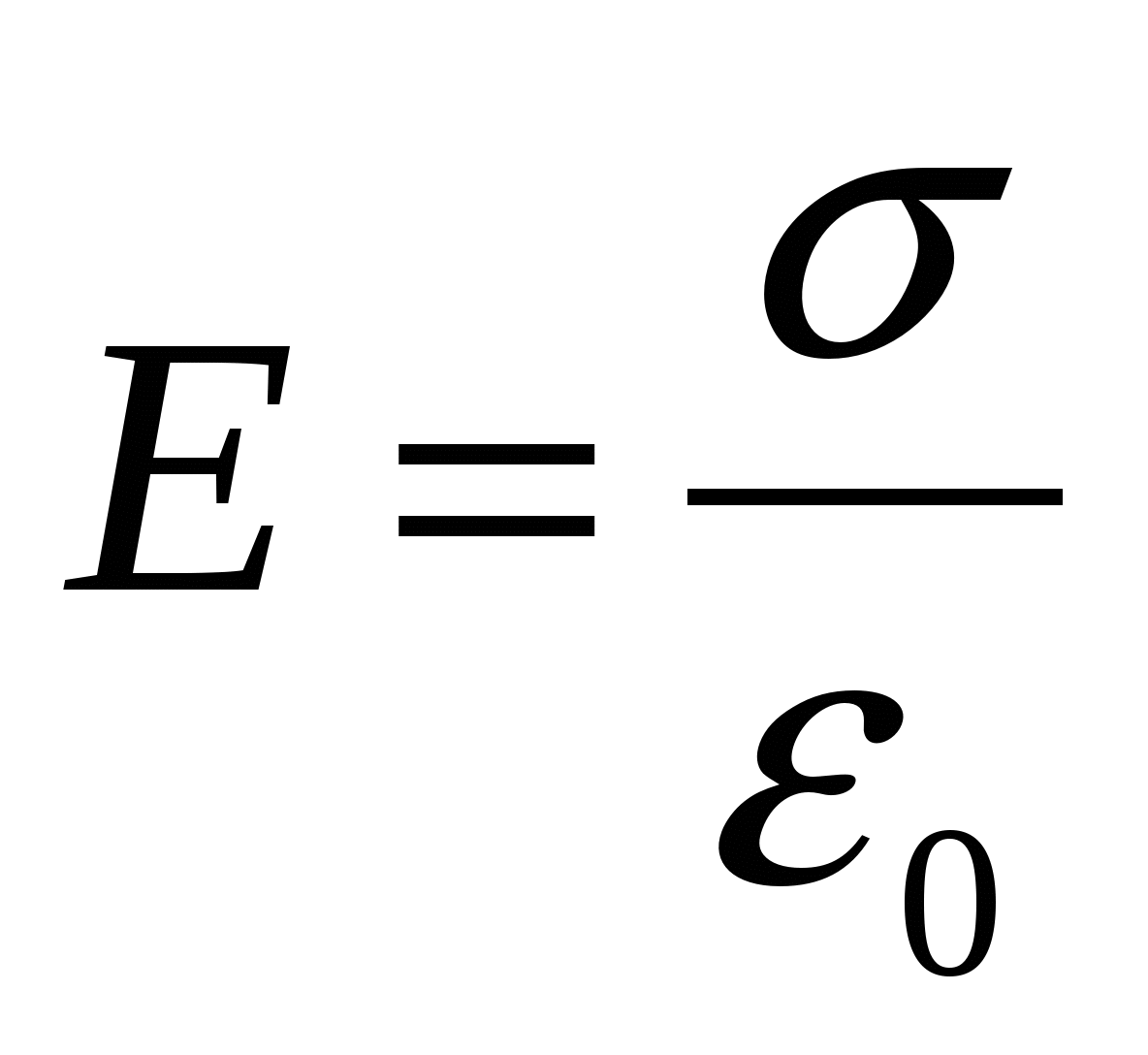 .
.
Similarly, it can be shown that if the planes are charged with the same name, then in the outer regions I and III the field strength is determined by the formula (11.I5), and in the inner region I, which is used for electrostatic protection of devices.
11.5.3. The field strength of an infinite uniformly charged filament with a linear charge density
 [
C/m ]
[
C/m ]
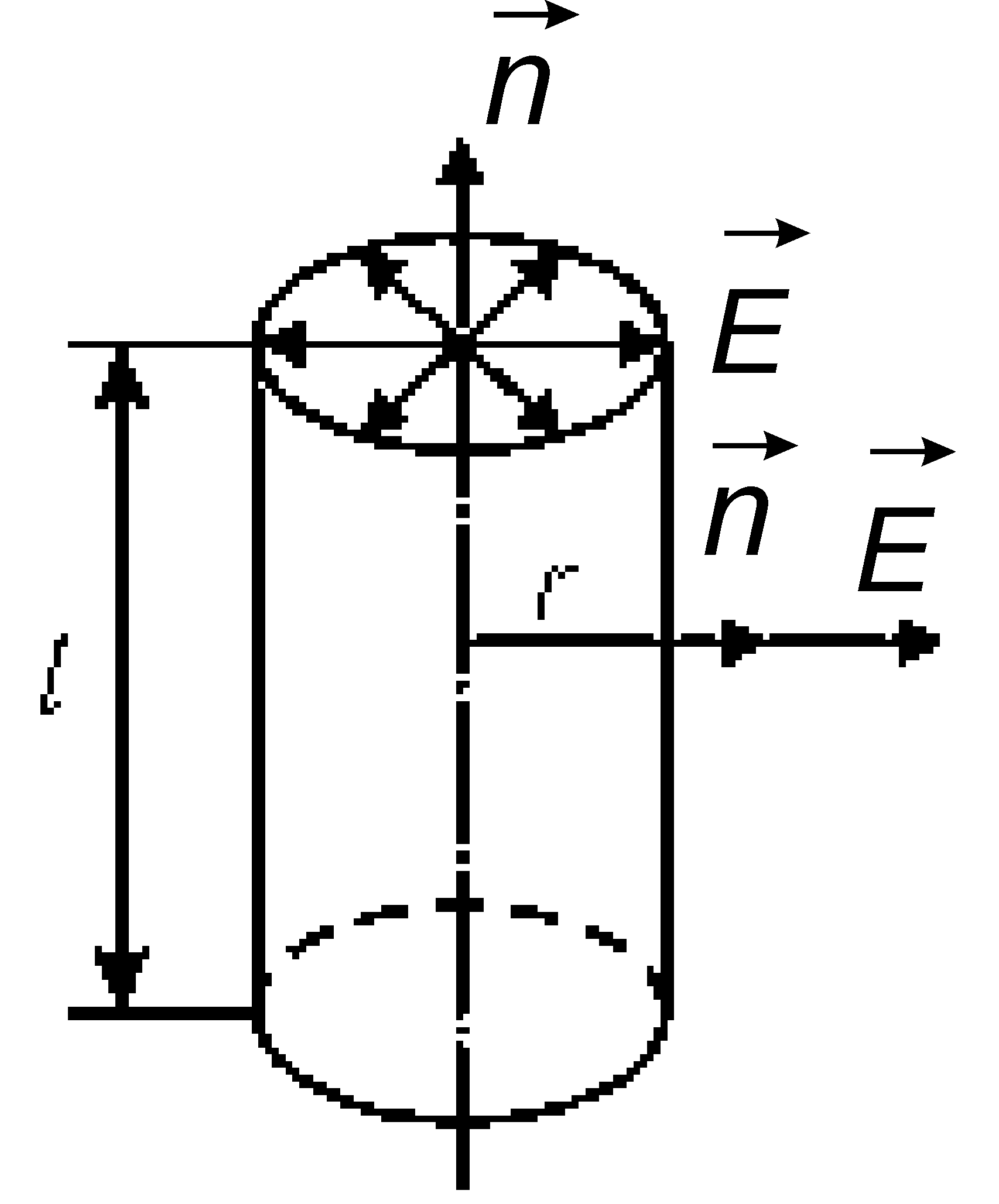
Rice. 1.10
 . . | (1.16) |
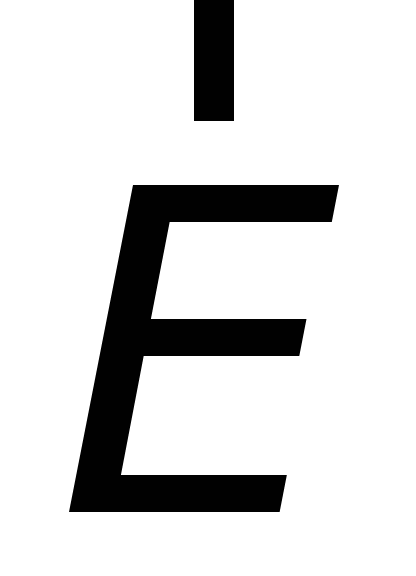 is perpendicular to the thread and therefore the flow of the vector through the bases of the cylinder is equal to zero.
is perpendicular to the thread and therefore the flow of the vector through the bases of the cylinder is equal to zero. where is the angle between the force  and direction of movement
and direction of movement 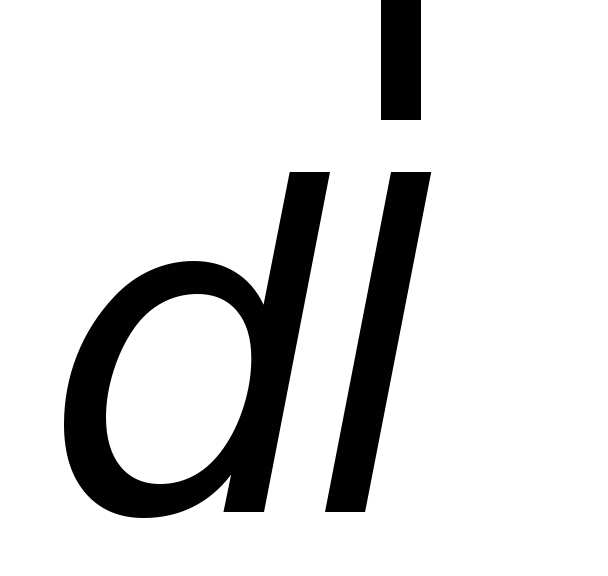 .
.
From fig. 1.11 shows that 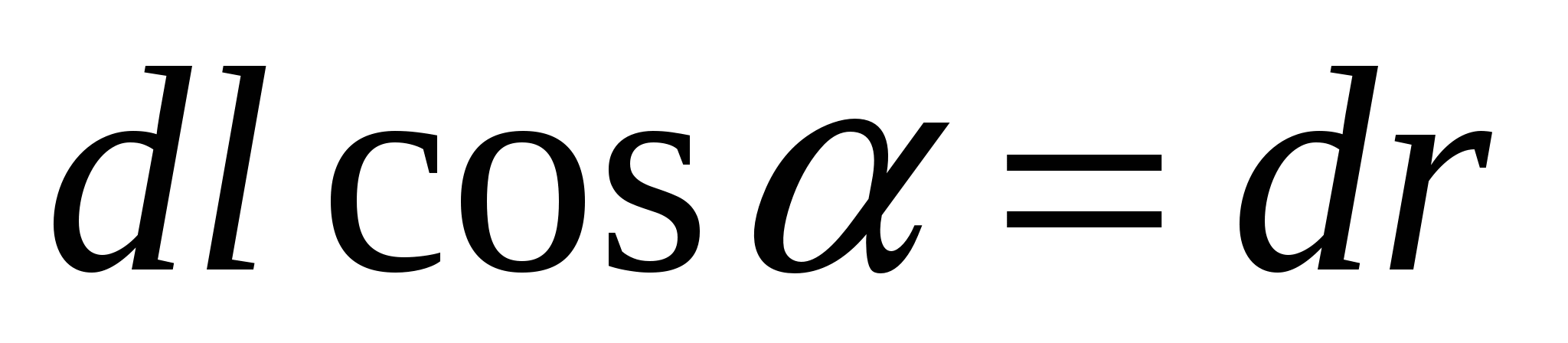 .That's why
.That's why 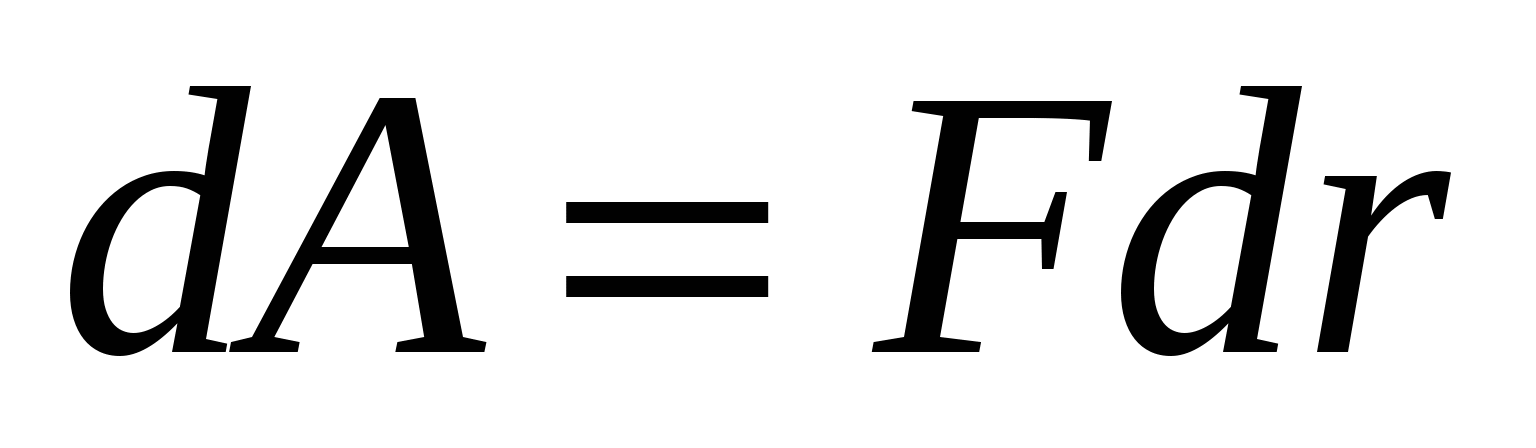
The total work but moving the charge q from a point A exactly B we obtain by integrating the expression (11.17). Using Coulomb's law, we get 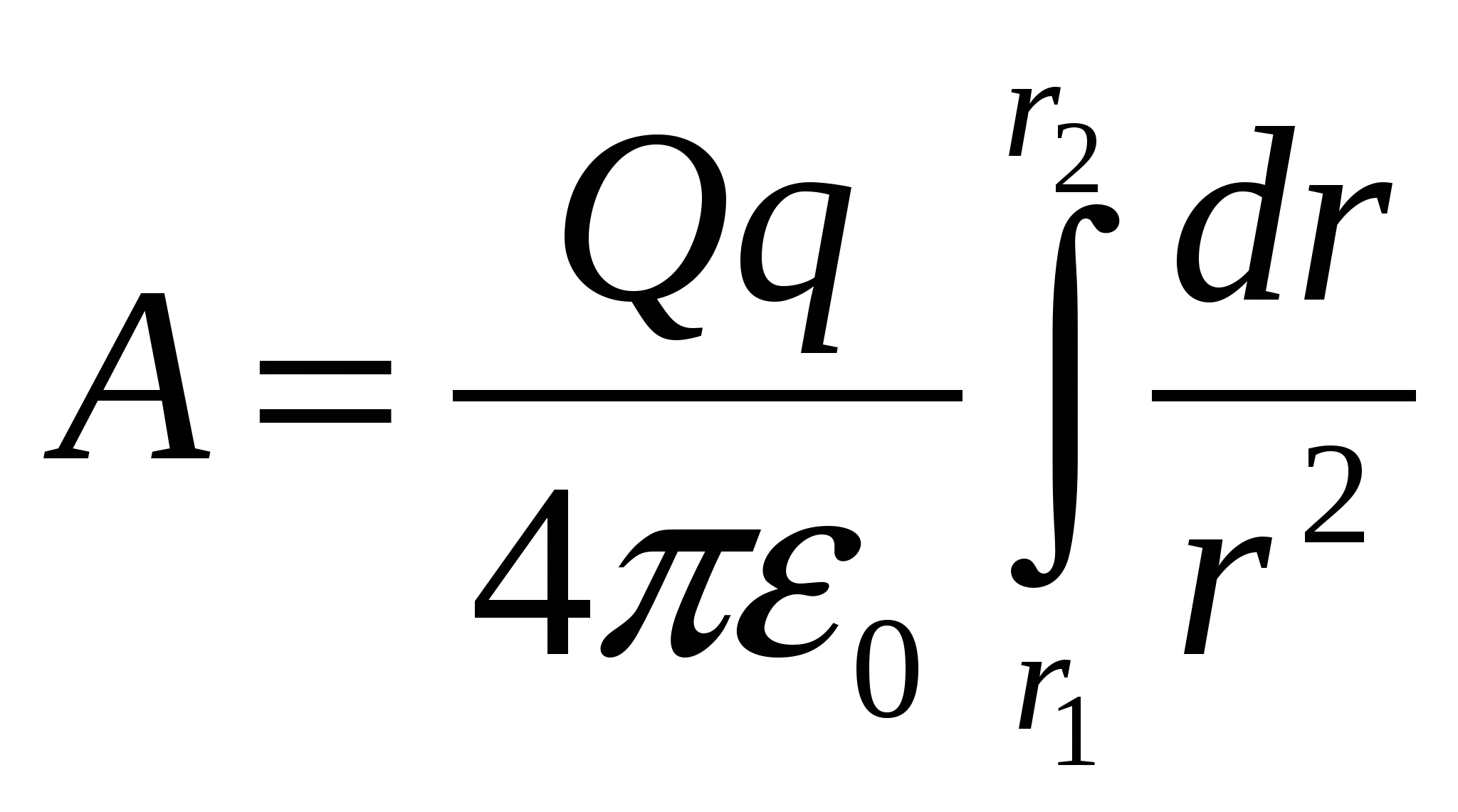 . Finally
. Finally
 , (1.18)
, (1.18)
If a charge moves from a point A exactly B on a different path, then, having done the same calculations, we again come to the formula (11.18). Therefore, work in an electrostatic field does not depend on the shape of the path, but depends only on the choice of the starting and ending points. In addition, as can be seen from (11.18), the work of moving a charge in an electrostatic hearth along a closed loop is zero, i.e. 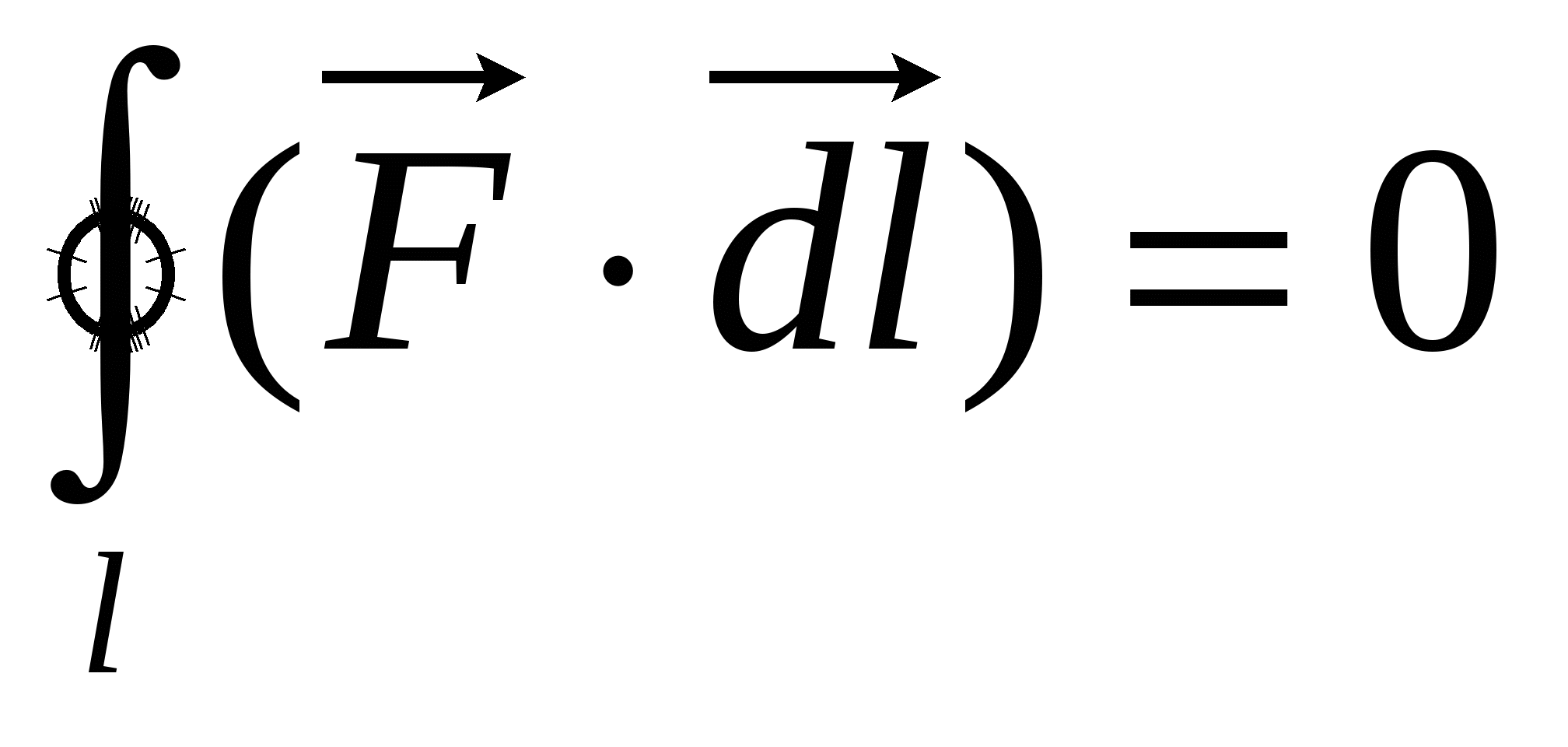 , (1.19)
, (1.19)
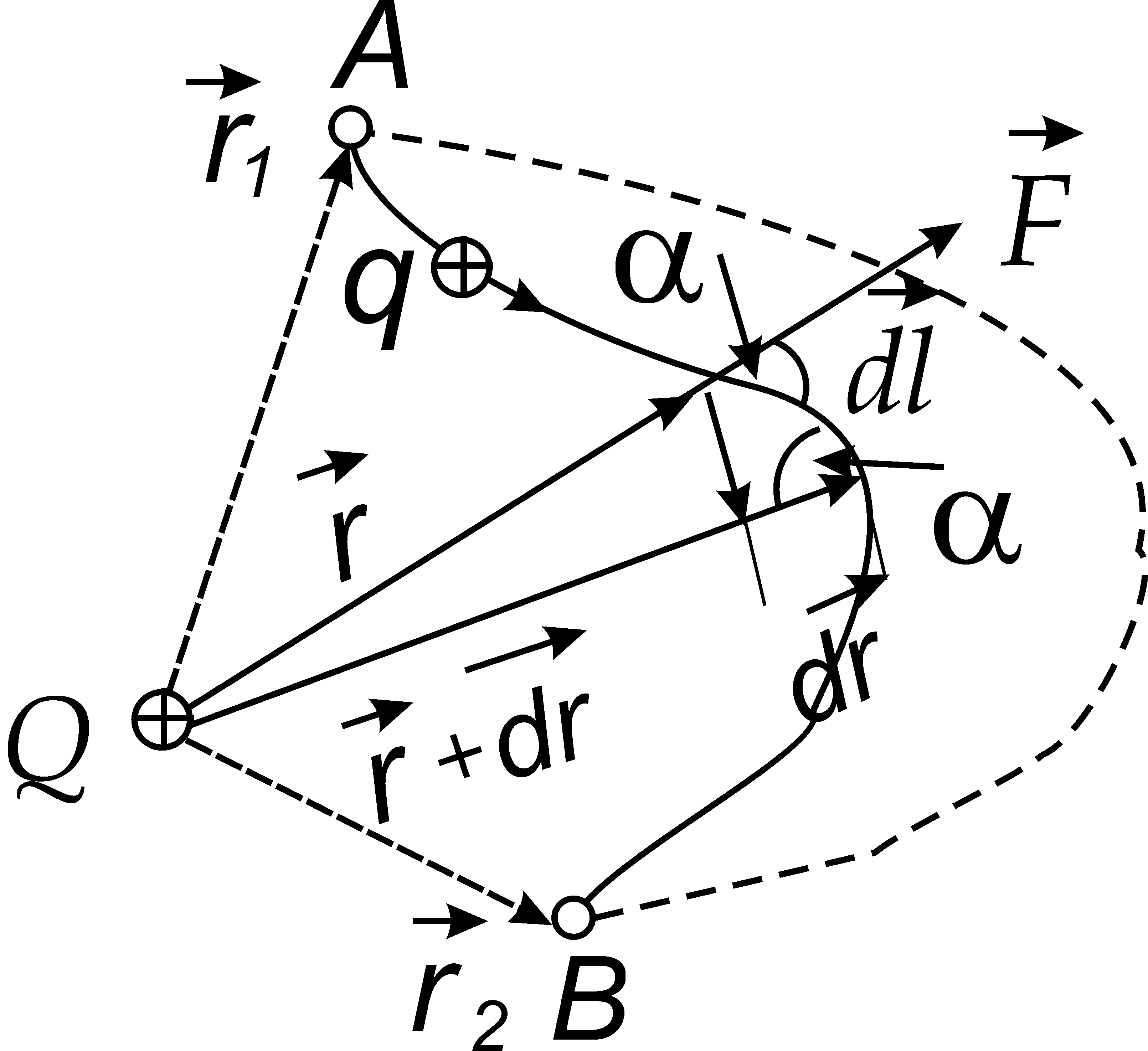
Rice. 1.11
These signs mean that the electrostatic field is potential. In accordance with the result obtained in § 3.3, the work of potential (conservative) forces can be expressed in terms of the potential energy difference:
From comparison (11.18) and (11.20) we conclude that the potential energy of interaction of two point charges
The unit of potential for an electrostatic field is the volt. One volt is the potential of such a point in the field at which a charge of 1 C has a potential energy of 1 J: 1 V \u003d 1 J / C.
We find the field potential of a point charge by substituting (1.21) into (1.22):
 . . | (1.23) |
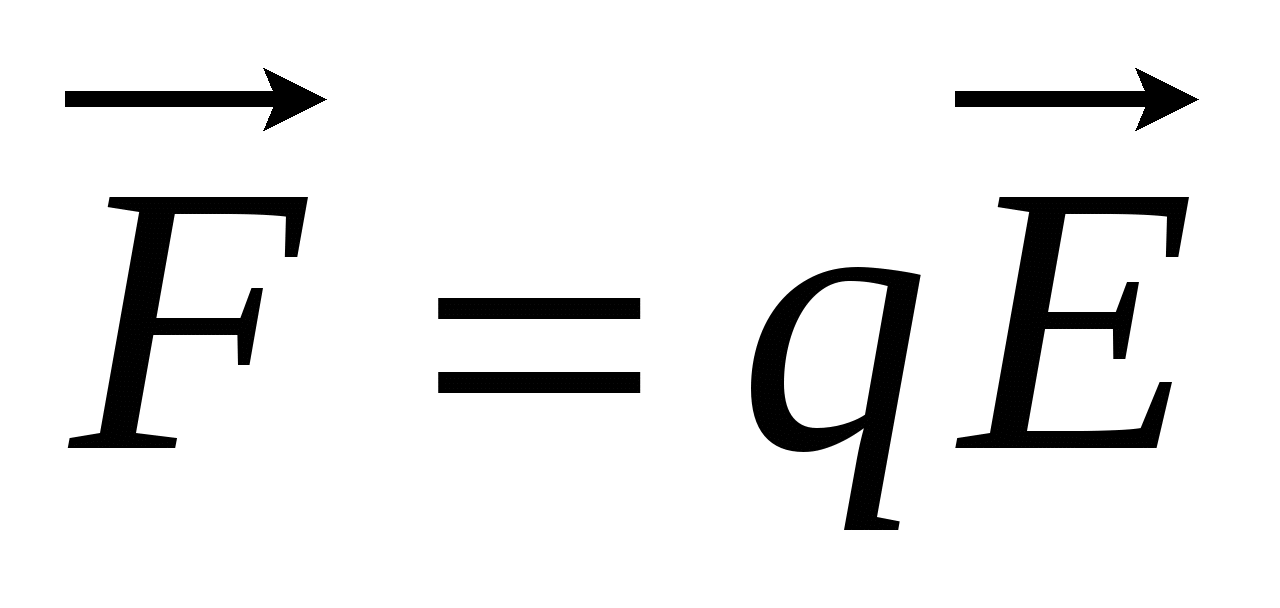 ,
, then we get
then we get  , (1.28)
, (1.28)those. the strength of the electrostatic field is equal to the potential gradient, taken with the sign "-". The sign "-" indicates that the field strength is directed towards the decrease in potential.
Let us introduce the concept of an equipotential surface, i.e. surface, at any point of which the value of the potential is the same: φ =const. For the field of a point charge, equipotential surfaces are spherical, for a uniformly charged thread - cylindrical, etc. The field strength vector is always perpendicular to the equipotential surface.
If the potential is a function of only one coordinate x, then expression (1.28) is simplified:
For a uniform electrostatic field (for example, the field of a flat capacitor), expression (2.30) is simplified:
Let us illustrate the application of formula (11.32) with examples.
1. Field of a point charge
3. The field of an electric dipole at a perpendicular to its axis
5. Capacitor field
| . | (1.37) |