Сходи. Вхідна група. Матеріали. Двері. Замки. Дизайн

Межі та безперервність

Безліч

Під безліччюрозуміється сукупність однорідних об'єктів. Об'єкти, які утворюють безліч, називаються елементамиабо точкамицієї множини. Багато позначають великими літерами, які елементи – малими. Якщо aє елементом множини A, то використовується запис aÎ A. Якщо bне є елементом множини A, то це записується так: b Ï A. Безліч, яке містить жодного елемента, називається порожнім безліччю і позначається так: Ø.

Якщо безліч Bскладається з частини елементів множини Aабо збігається з ним, то безліч Bназивають підмножиноюмножини і позначають BÌ A.

Дві множини називають рівнимиякщо вони складаються з тих самих елементів.

Об'єднаннямдвох множин Aі Bназивається безліч C, Що складається з усіх елементів, що належать хоча б одному з множин: C=AÈ B.

Перетиномдвох множин Aі Bназивається безліч C, Що складається з усіх елементів, що належать кожному з даних множин: C=AÇ B.

Різницямножин Aі Bназивається безліч E A, які не належать безлічі B: .

Доповненнямбезлічі AÌ Bназивається безліч C, Що складається з усіх елементів множини B, що не належать A.

Багато, елементами яких є дійсні числа, називаються числовими:

При цьому NÌ ZÌ QÌ R, IÌ Rі R=IÈ Q.

Безліч X, елементи якого задовольняють нерівності називається відрізком(сегментом) і позначається [ a; b]; нерівності a<x<b – інтерваломі позначається (); нерівностям та - напівінтерваламита позначаються відповідно і . Також часто доводиться мати справу з нескінченними інтервалами та напівінтервалами: , , , та . Усі їх зручно називати проміжками .

Інтервал, тобто. безліч точок, що задовольняють нерівності (де ), називається околицею точки a.

Концепція функції. Основні властивості функції

Якщо кожному елементу xбезлічі Xставиться у відповідність єдиний елемент yбезлічі Y, то кажуть, що на безлічі Xзадана функція y=f(x). При цьому xназивають незалежної змінноїабо аргументом, а y – залежною змінноюабо функцією, а fпозначає закон відповідності. Безліч Xназивають областю визначенняфункції, а безліч Y – областю значеньфункції.

Існує кілька способів завдання функцій.

1) Аналітичний метод – функція задається формулою виду y=f(x).

2) Табличний спосіб – функція задається таблицею, що містить значення аргументу та відповідні їм значення функції y=f(x).

3) Графічний метод – зображення графіка функції, тобто. безлічі точок ( x; y) координатної площини, абсциси яких представляють значення аргументу , а ординати – відповідні значення функції y=f(x).

4) Словесний метод – функція описується правилом її складання. Наприклад, функція Діріхле набуває значення 1, якщо x– раціональне число та 0, якщо x- Ірраціональне число.

Вирізняють такі основні властивості функцій.

1 Парність та непарністьФункція y=f(x) називається парноїякщо для будь-яких значень xв галузі її визначення виконується f(–x)=f(x), і непарною, якщо f(–x)=–f(x). Якщо не виконується жодна з перерахованих рівностей, то y=f(x) називається функцією загального вигляду. Графік парної функції симетричний щодо осі Ой, А графік непарної функції симетричний щодо початку координат.

2 МонотонністьФункція y=f(x) називається зростаючою (спадаючою) на проміжку X, якщо більшого значенняаргумент з цього проміжку відповідає більше (менше) значення функції. Нехай x 1 ,x 2 Î X, x 2 >x 1 . Тоді функція зростає на проміжку X, якщо f(x 2)>f(x 1), і зменшується, якщо f(x 2)<f(x 1).

Поряд із зростаючими та спадними функціями розглядають незменшуючі та незростаючі функції. Функція називається невпадаючою (незростаючою), якщо при x 1 ,x 2 Î X, x 2 >x 1 виконується нерівність f(x 2)≥f(x 1) (f(x 2)≤f(x 1)).

Зростаючі та спадні функції, а також незростаючі та незменшувальні функції називають монотонними.

3 ОбмеженістьФункція y=f(x) називається обмеженою на проміжку Xякщо існує таке позитивне число M>0, що | f(x)|≤Mдля будь-кого xÎ X. В іншому випадку функція називається необмеженою на X.

4 ПеріодичністьФункція y=f(x) називається періодичною з періодом T≠0, якщо для будь-яких xз області визначення функції f(x+T)=f(x). Надалі під періодом розумітимемо найменший позитивний період функції.

Функція називається явнийякщо вона задана формулою виду y=f(x). Якщо функція задана рівнянням F(x, y)=0, не дозволеним щодо залежної змінної y, то її називають неявний.

Нехай y=f(x) є функція від незалежної змінної , визначена на множині Xз областю значень Y. Поставимо у відповідність кожному yÎ Yєдине значення xÎ X, за якого f(x)=y. Тоді отримана функція x=φ (y), визначена на безлічі Yз областю значень X, називається зворотнійі позначається y=f –1 (x). Графіки взаємно зворотних функцій симетричні щодо бісектриси першої та третьої координатних чвертей.

Нехай функція y=f(u) є функція змінної u, визначеної на безлічі Uз областю значень Y, а змінна uу свою чергу є функцією u=φ (x), визначеної на безлічі Xз областю значень U. Тоді задана на безлічі Xфункція y=f(φ (x)) називається складною функцією(Композицією функцій, суперпозицією функцій, функцією від функції).

Елементарні функції

До основних елементарних функцій відносять:

• статечну функцію y=x n; y=x – nі y=x 1/ n;
• показову функцію y=a x;
• логарифмічну функцію y=log a x;
• тригонометричні функції y=sin x, y=cos x, y=tg xі y=ctg x;
• зворотні тригонометричні функції y= arcsin x, y=arccos x, y=arctg xі y= arcctg x.

З основних елементарних функцій нові функції можуть бути отримані за допомогою дій алгебри і суперпозицією функцій.

Функції, побудовані з основних елементарних функцій за допомогою кінцевого числа дій алгебри та кінцевого числа операцій суперпозиції, називаються елементарними.

Алгебраїчноюназивається функція, у якій над аргументом проводиться кінцеве число дій алгебри. До алгебраїчних функцій відносяться:

· Ціла раціональна функція (багаточлен або поліном)

· Дробально-раціональна функція (відношення двох багаточленів)

· Ірраціональна функція (якщо у складі операцій над аргументом є вилучення кореня).

Будь-яка неалгебраїчна функція називається трансцендентної. До трансцендентних функцій відносяться показова, логарифмічна, тригонометричні, зворотні тригонометричні функції.

1) Область визначення функції та область значень функції.

Область визначення функції - це безліч усіх допустимих дійсних значеньаргументу x(змінною x), при яких функція y = f(x)визначено. Область значень функції - це безліч усіх дійсних значень y, що приймає функцію.

В елементарної математики вивчаються функції лише з безлічі дійсних чисел.

2) Нулі функції.

Нуль функції – таке значення аргументу, При якому значення функції дорівнює нулю.

3) Проміжки знакостійності функції.

Проміжки знакостійності функції – такі безлічі значень аргументу, у яких значення функції лише позитивні чи лише негативні.

4) Монотонність функції.

Зростаюча функція (у певному проміжку) - функція, яка має більшому значенню аргументу з цього проміжку відповідає більше значення функції.

Зменшуюча функція (у деякому проміжку) - функція, яка має більшому значенню аргументу з цього проміжку відповідає менше значення функції.

5) парність (непарність) функції.

Четна функція - функція, у якої область визначення симетрична щодо початку координат та для будь-якого хв галузі визначення виконується рівність f(-x) = f(x).

Графік парної функції симетричний щодо осі ординат. хНепарна функція - функція, у якої область визначення симетрична щодо початку координат та для будь-якого в галузі визначення справедлива рівність f(-x) = - f(x

)..

Графік непарної функції симетричний щодо початку координат.

6) Обмежена та необмежена функції.

Функція називається обмеженою, якщо є таке позитивне число M, що |f(x)| ≤ M для всіх значень x. Якщо такої кількості немає, то функція - необмежена.

7) Періодичність функції Функція f(x) - періодична, якщо існує таке відмінне від нуля число T, що для будь-якого x з області визначення функції має місце: f(x+T) = f(x). Таке найменше називається періодом функції. Усі тригонометричні функції є періодичними. (Тригонометричні формули). 19. Основні

елементарні функції

, їх властивості та графіки. Застосування функцій економіки.

Основні елементарні функції. Їх властивості та графіки 1. Лінійна функція.

Лінійною функцією називається функція виду , де х - змінна, а і b - дійсні числа.Число аназивають

кутовим коефіцієнтом

прямий, він дорівнює тангенсу кута нахилу цієї прямої до позитивного напрямку осі абсцис. Графік лінійної функції є пряма лінія. Вона визначається двома точками.

Властивості лінійної функції

1. Область визначення - безліч всіх дійсних чисел: Д(y) = R

2. Безліч значень - безліч всіх дійсних чисел: Е(у) = R

3. Функція набуває нульового значення при або.

4. Функція зростає (зменшується) по всій області визначення.

5. Лінійна функція безперервна по всій області визначення, диференційована і . 2. Квадратична функція.

Функція виду , де х – змінна, коефіцієнти а, b, с – дійсні числа, називаєтьсяквадратичні. RОбласть визначення та область значень функції. XВ елементарній математиці вивчаються функції лише на безлічі дійсних чисел x.Це означає, що аргумент функції може набувати ті дійсні значення, у яких функція визначена, тобто. вона також набуває лише дійсних значень. Безліч y= f(xвсіх допустимих дійсних значень аргументу , при яких функція)визначена, називається Yобластю визначення функції y. Безліч всіх дійсних значень, які приймає функція, називається областю значень функції. Тепер можна надати більш точне визначення функції:, за яким для кожного елемента з множиниX можна знайти один і тільки один елемент з множини Y, називається функцією.

З цього визначення випливає, що функція вважається заданою, якщо:

Задано область визначення функції X ;

Задано область значень функції Y ;

Відомо правило (закон) відповідності, причому таке, що для кожного

Значення аргументу можна знайти лише одне значення функції.

Ця вимога однозначності функції є обов'язковою.

Монотонна функція.Якщо для будь-яких двох значень аргументу x 1 та x 2 з умови x 2 > x 1 слід f(x 2) > f(x 1), то функція f(x) називається зростаючою; якщо для будь-яких x 1 та x 2 з умови x 2 > x 1 слід f(x 2) < f(x 1), то функція f(x) називається спадаючою. Функція, яка тільки зростає або лише зменшується, називається монотонної.

Обмежена та необмежена функції.Функція називається обмеженоюякщо існує таке позитивне число M, що | f(x) | Mдля всіх значень x.Якщо такої кількості немає, то функція - необмежена.

Приміри.

Функція, зображена на рис.3 є обмеженою, але не монотонною. Функція на рис.4 - саме навпаки, монотонна, але необмежена. (Поясніть це, будь ласка!).

Безперервна та розривна функції.Функція y = f (x) називається безперервний у точціx = a, якщо:

1) функція визначена при x = a, Тобто. f (a) існує;

2) існує кінцевиймежа lim f (x) ;

x→a

(Див. «Межі функцій»)

3) f (a) = lim f (x) .

x→a

Якщо не виконується хоча б одна з цих умов, то функція називається розривнийу точці x = a.

Якщо функція безперервна у всіх точках своєї галузі визначення, то вона називається безперервною функцією.

Парна та непарна функції.Якщо для будь-якого x f(- x) = f (x), то функція називається парної;якщо має місце: f(- x) = - f (x), то функція називається непарний. Графік парної функціїсиметричний щодо осі Y(рис.5), а графік непарної функції цимметричний щодо початку координат(Рис.6).

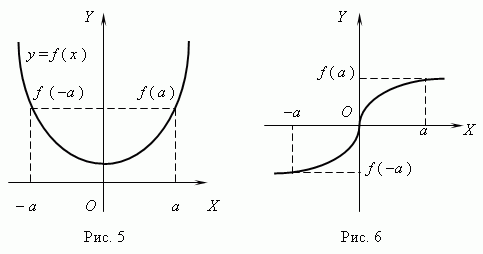
Періодична функція.Функція f (x) - періодичнаякщо існує таке відмінне від нулячисло T, що для будь-якого xв галузі визначення функції має місце: f (x + T) = f (x). Таке найменшечисло називається періодом функції. Усі тригонометричні функції є періодичними.

П р і м е р 1 . Довести, що sin xмає період 2 .

Рішення. Ми знаємо, що sin ( x+ 2n) = sin x, де n= 0, ± 1, ± 2, …

Отже, додавання 2 nдо аргументу синуса не

Змінює його значення. Чи існує інше число з таким

А якістю?

Припустимо, що P- Таке число, тобто. рівність:

Sin ( x+ P) = sin x,

Справедливо для будь-якого значення x. Але тоді воно має

Місце і при x= / 2, тобто.

Sin (/ 2 + P) = sin / 2 = 1.

Але за формулою приведення sin (/2 + P) = cos P. Тоді

З двох останніх рівностей випливає, що cos P= 1, але ми

Знаємо, що це правильно лише за P = 2n. Оскільки найменшим

Відмінним від нуля числом із 2 nє 2, то це число

І є період sin x. Аналогічно доводиться, що 2з nє , таким чином, це період 2 x.

Нулі функції.Значення аргументу, у якому функція дорівнює 0, називається нулем (коренем) функції. Функція може мати кілька нулів.Наприклад, функція y = x (x + 1) (x-3) має три нулі: x= 0, x= -1, x= 3. Геометрично нуль функції - це абсциса точки перетину графіка функції з віссю Х .

На рис.7 представлений графік функції з нулями: x= a, x = bі x= c.

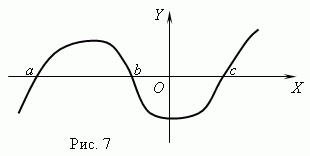
Асимптота.Якщо графік функції необмежено наближається до деякої прямої при віддаленні від початку координат, то ця пряма називається асимптотою.

Представлені властивості та графіки статечних функцій при різних значенняхпоказника ступеня. Основні формули, області визначення та безлічі значень, парність, монотонність, зростання та спадання, екстремуми, опуклість, перегини, точки перетину з осями координат, межі, приватні значення.

Формули зі статечною функцією

На області визначення статечної функції y = x p мають місце такі формули:
; ;
;
; ;
; ;
; .

Властивості статечних функцій та їх графіки

Ступінна функція з показником рівним нулю, p = 0

Якщо показник статечної функції y = x p дорівнює нулю, p = 0, то статечна функція визначена для всіх x ≠ 0 і є постійною рівною одиниці:
y = x p = x 0 = 1, x ≠ 0 .

Ступінна функція з натуральним непарним показником, p = n = 1, 3, 5, ...

Розглянемо статечну функцію y = x p = x n з натуральним непарним показником ступеня n = 1, 3, 5, ....

Такий показник також можна записати у вигляді: n = 2k + 1 де k = 0, 1, 2, 3, ... - ціле не негативне. Нижче наведено властивості та графіки таких функцій.

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... . -∞ < x < ∞
Область визначення: -∞ < y < ∞
Безліч значень:Парність:
непарна, y(-x) = - y(x)Монотонність:
монотонно зростаєЕкстремуми:
ні
Випуклість:< x < 0 выпукла вверх
при -∞< x < ∞ выпукла вниз
при 0Точки перегинів:
Точки перегинів:
x = 0, y = 0
;
Межі:
Приватні значення:
при x = -1
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
за x = 0, y(0) = 0 n = 0
за x = 1, y(1) = 1 n = 1
Зворотня функція:
при n = 1 , функція є зворотною до самої себе: x = y

при n ≠ 1 зворотною функцією є корінь ступеня n :

Ступінна функція з натуральним парним показником, p = n = 2, 4, 6, ...

Графік статечної функції y = x n з натуральним парним показником за різних значень показника ступеня n = 2, 4, 6, ... .

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... . -∞ < x < ∞
Область визначення: 0 ≤ y< ∞
Безліч значень:парна, y(-x) = y(x)
непарна, y(-x) = - y(x)
при x ≤ 0 монотонно зменшується
при x ≥ 0 монотонно зростає
монотонно зростаємінімум, x = 0, y = 0
нівипукла вниз
при 0Екстремуми:
Точки перетину з осями координат:Точки перегинів:
x = 0, y = 0
;
Межі:
при x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
за x = 0, y(0) = 0 n = 0
за x = 1, y(1) = 1 n = 1
при n = 2 квадратний корінь:
при n ≠ 2, корінь ступеня n:

Ступінна функція з цілим негативним показником, p = n = -1, -2, -3, ...

Розглянемо статечну функцію y = x p = x n з цілим негативним показником ступеня n = -1, -2, -3, ....

Якщо покласти n = -k де k = 1, 2, 3, ... - натуральне, то її можна представити у вигляді:

Графік статечної функції y = x n з цілим негативним показником за різних значень показника ступеня n = -1, -2, -3, ... .

Непарний показник, n = -1, -3, -5, ...

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Нижче представлені властивості функції y = x n з непарним негативним показником n = -1, -3, -5, ....
Область визначення: x ≠ 0
Безліч значень:Парність:
непарна, y(-x) = - y(x) y ≠ 0
монотонно зростаєЕкстремуми:
ні
монотонно зменшується< 0 : выпукла вверх
при x
при 0Екстремуми:
Точки перетину з осями координат:Екстремуми:
при x > 0: опукла вниз
монотонно зменшується< 0, y < 0
Знак:
x = 0, y = 0
; ; ;
Межі:
за x = 0, y(0) = 0 n = 0
за x = 1, y(1) = 1 n = 1
при x>0, y>0
при n = -1< -2 ,

при n

Чітний показник, n = -2, -4, -6, ...

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Нижче представлені властивості функції y = x n з непарним негативним показником n = -1, -3, -5, ....
Область визначення:Нижче представлені властивості функції y = x n з парним негативним показником n = -2, -4, -6, ....
Безліч значень:парна, y(-x) = y(x)
непарна, y(-x) = - y(x)
монотонно зменшується< 0 : монотонно возрастает
y > 0
монотонно зростаєЕкстремуми:
нівипукла вниз
при 0Екстремуми:
Точки перетину з осями координат:Екстремуми:
при x > 0: опукла внизНижче представлені властивості функції y = x n з парним негативним показником n = -2, -4, -6, ....
x = 0, y = 0
; ; ;
Межі:
за x = 0, y(0) = 0 n = 0
за x = 1, y(1) = 1 n = 1
при x > 0: монотонно зменшується
при n = -1< -2 ,

при n = -2

Ступенева функція з раціональним (дрібним) показником Розглянемо статечну функцію y = x p з раціональним (дрібним) показником ступеня, де n – ціле, m > 1 – натуральне. Причому n, m не мають.

спільних дільників

Знаменник дробового показника – непарний

Нехай знаменник дрібного показника ступеня непарний: m = 3, 5, 7, ... . У цьому випадку статечна функція x p визначена як для позитивних, так і для негативних значень аргументу x .< 0

Розглянемо властивості таких статечних функцій, коли p знаходиться в певних межах. Показник p негативний, p: .

Нехай раціональний показник ступеня (з непарним знаменником m = 3, 5, 7, ...)

менше нуля

Графіки статечних функцій з раціональним негативним показником при різних значеннях показника ступеня , де m = 3, 5, 7 ... - непарне.

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Нижче представлені властивості функції y = x n з непарним негативним показником n = -1, -3, -5, ....
Область визначення: x ≠ 0
Безліч значень:Парність:
непарна, y(-x) = - y(x) y ≠ 0
монотонно зростаєЕкстремуми:
ні
монотонно зменшується< 0 : выпукла вверх
при x
при 0Екстремуми:
Точки перетину з осями координат:Екстремуми:
при x > 0: опукла вниз
монотонно зменшується< 0, y < 0
Знак:
x = 0, y = 0
; ; ;
Межі:
Непарний чисельник, n = -1, -3, -5, ...
за x = 0, y(0) = 0 n = 0
за x = 1, y(1) = 1 n = 1

Наводимо властивості статечної функції y = x p з раціональним негативним показником , де n = -1, -3, -5, ... - непарне негативне ціле, m = 3, 5, 7 ... - непарне натуральне.

Властивості статечної функції y = x p з раціональним негативним показником , де n = -2, -4, -6, ... - парне негативне ціле, m = 3, 5, 7 ... - непарне натуральне.

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Нижче представлені властивості функції y = x n з непарним негативним показником n = -1, -3, -5, ....
Область визначення:Нижче представлені властивості функції y = x n з парним негативним показником n = -2, -4, -6, ....
Безліч значень:парна, y(-x) = y(x)
непарна, y(-x) = - y(x)
монотонно зменшується< 0 : монотонно возрастает
y > 0
монотонно зростаєЕкстремуми:
нівипукла вниз
при 0Екстремуми:
Точки перетину з осями координат:Екстремуми:
при x > 0: опукла внизНижче представлені властивості функції y = x n з парним негативним показником n = -2, -4, -6, ....
x = 0, y = 0
; ; ;
Межі:
при x = -1, y(-1) = (-1) n = 1
за x = 0, y(0) = 0 n = 0
за x = 1, y(1) = 1 n = 1

Показник p позитивний, менше одиниці, 0< p < 1

Графік статечної функції з раціональним показником (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.

Непарний чисельник, n = 1, 3, 5, ...

< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... . -∞ < x < +∞
Область визначення: -∞ < y < +∞
Безліч значень:Парність:
непарна, y(-x) = - y(x)Монотонність:
монотонно зростаєЕкстремуми:
ні
монотонно зменшується< 0 : выпукла вниз
при x > 0: опукла вгору
при 0Точки перегинів:
Точки перетину з осями координат:Точки перегинів:
при x > 0: опукла вниз
монотонно зменшується< 0, y < 0
Знак:
x = 0, y = 0
;
Межі:
за x = -1, y(-1) = -1
за x = 0, y(0) = 0
за x = 1, y(1) = 1
за x = 1, y(1) = 1 n = 1

Чітний чисельник, n = 2, 4, 6, ...

Представлені властивості статечної функції y = x p з раціональним показником, що знаходиться в межах 0< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... . -∞ < x < +∞
Область визначення: 0 ≤ y< +∞
Безліч значень:парна, y(-x) = y(x)
непарна, y(-x) = - y(x)
монотонно зменшується< 0 : монотонно убывает
при x > 0: монотонно зростає
монотонно зростаємінімум при x = 0, y = 0
ніопукла вгору при x ≠ 0
при 0Екстремуми:
Точки перетину з осями координат:Точки перегинів:
при x > 0: опукла внизпри x ≠ 0, y > 0
x = 0, y = 0
;
Межі:
за x = -1, y(-1) = 1
за x = 0, y(0) = 0
за x = 1, y(1) = 1
за x = 1, y(1) = 1 n = 1

Показник p більше одиниці, p > 1

Графік статечної функції з раціональним показником (p > 1) при різних значеннях показника ступеня, де m = 3, 5, 7, ... - непарне.

Непарний чисельник, n = 5, 7, 9, ...

Властивості статечної функції y = x p з раціональним показником, більшим за одиницю: .

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... . -∞ < x < ∞
Область визначення: -∞ < y < ∞
Безліч значень:Парність:
непарна, y(-x) = - y(x)Монотонність:
монотонно зростаєЕкстремуми:
ні
Випуклість:< x < 0 выпукла вверх
при -∞< x < ∞ выпукла вниз
при 0Точки перегинів:
Точки перетину з осями координат:Точки перегинів:
x = 0, y = 0
;
Межі:
за x = -1, y(-1) = -1
за x = 0, y(0) = 0
за x = 1, y(1) = 1
за x = 1, y(1) = 1 n = 1

Де n = 5, 7, 9, ... - непарне натуральне, m = 3, 5, 7 ... - непарне натуральне.

Чітний чисельник, n = 4, 6, 8, ...

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... . -∞ < x < ∞
Область визначення: 0 ≤ y< ∞
Безліч значень:парна, y(-x) = y(x)
непарна, y(-x) = - y(x)
монотонно зменшується< 0 монотонно убывает
Властивості статечної функції y = x p з раціональним показником, більшим за одиницю: .
монотонно зростаємінімум при x = 0, y = 0
нівипукла вниз
при 0Екстремуми:
Точки перетину з осями координат:Точки перегинів:
x = 0, y = 0
;
Межі:
за x = -1, y(-1) = 1
за x = 0, y(0) = 0
за x = 1, y(1) = 1
за x = 1, y(1) = 1 n = 1

Де n = 4, 6, 8, … – парне натуральне, m = 3, 5, 7… – непарне натуральне.

при x>0 монотонно зростає

Знаменник дробового показника – парний

Нехай знаменник дробового показника ступеня парний: m = 2, 4, 6, .... У цьому випадку статечна функція x p не визначена для негативних значень аргументу. Її властивості збігаються з властивостями статечної функції з ірраціональним показником (див. наступний розділ).

Ступенева функція з ірраціональним показником

Розглянемо статечну функцію y = x p з ірраціональним показником ступеня p.< 0

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Властивості таких функцій відрізняються від розглянутих тим, що вони не визначені для негативних значень аргументу x .
Область визначення:Нижче представлені властивості функції y = x n з парним негативним показником n = -2, -4, -6, ....
непарна, y(-x) = - y(x) y ≠ 0
нівипукла вниз
при 0Екстремуми:
Точки перетину з осями координат:Екстремуми:
x = 0, y = 0 ;
Для позитивних значень аргументу властивості залежать тільки від величини показника ступеня p і не залежать від того, чи є р цілим, раціональним або ірраціональним. y = x p при різних значеннях показника p.

Ступінна функція з негативним показником p

x > 0< p < 1

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Приватне значення:
Область визначення:За x = 1, y(1) = 1 p = 1
непарна, y(-x) = - y(x)Монотонність:
ніСтупенева функція з позитивним показником p > 0
при 0Екстремуми:
Точки перетину з осями координат:Точки перегинів:
x = 0, y = 0
Межі:Показник менше одиниці 0
y = x p при різних значеннях показника p.

x ≥ 0

Графік статечної функції y = x n з натуральним непарним показником за різних значень показника ступеня n = 1, 3, 5, ... .Приватне значення:
Область визначення:За x = 1, y(1) = 1 p = 1
непарна, y(-x) = - y(x)Монотонність:
нівипукла вниз
при 0Екстремуми:
Точки перетину з осями координат:Точки перегинів:
x = 0, y = 0
Межі:Показник менше одиниці 0
y = x p при різних значеннях показника p.

y ≥ 0
випукла вгору

Російська гімназія

КОНСПЕКТ

Виконав

учень 10 "Ф" класу Бурмістрів Сергій

Керівник

вчитель математики

Юліна О.А.

Нижній Новгород

Функція та її властивості

Функція-залежність змінної увід змінної x , якщо кожному значенню хвідповідає єдине значення у .

Змінна х-незалежна змінна чи аргумент.

Змінна у-залежна змінна

Значення функції-значення у, що відповідає заданому значенню х .

Область визначення функції-всі значення, які набуває незалежна змінна.

Область значень функції (безліч значень)-всі значення, які набуває функція.

Функція є парною-якщо для будь-кого х f(x)=f(-x)

Функція є непарною-якщо для будь-кого хв галузі визначення функції виконується рівність f(-x)=-f(x)

Зростаюча функція-якщо для будь-яких х 1і х 2 ,таких, що х 1 < х 2, виконується нерівність f( х 1 ) х 2 )