Паралельне перенесення.
ПЕРЕНОС ВДОЛІ ОСІ ОРДИНАТ
f(x) => f(x) - b
Нехай потрібно збудувати графік функції у = f(х) - b. Неважко помітити, що ординати цього графіка всім значень x на |b| одиниць менше відповідних ординат графіка функцій у = f(х) при b>0 і |b| одиниць більше - при b 0 або нагору при b Для побудови графіка функції y + b = f(x) слід побудувати графік функції y = f(x) і перенести вісь абсцис на | b | одиниць вгору при b>0 чи |b| одиниць вниз у b
ПЕРЕНОС ВДОЛІ ОСІ АБСЦІСС
f(x) => f(x + a)
Нехай потрібно збудувати графік функції у = f(x + a). Розглянемо функцію y = f(x), яка у певній точці x = x1 набуває значення у1 = f(x1). Вочевидь, функція у = f(x + a) прийме таке значення в точці x2, координата якої визначається рівності x2 + a = x1, тобто. x2 = x1 - a, причому розглянута рівність справедливо для сукупності всіх значень з області визначення функції. Отже, графік функції у = f(x + a) може бути отриманий паралельним переміщенням графіка функції y = f(x) вздовж осі абсцис вліво |a| одиниць при a > 0 чи праворуч |a| одиниць при a Для побудови графіка функції y = f(x + a) слід побудувати графік функції y = f(x) і перенести вісь ординат на | одиниць вправо при a>0 чи |a| одиниць ліворуч у a
Приклади:
1.y=f(x+a)
2.y=f(x)+b
Відображення.
ПОБУДУВАННЯ ГРАФІКА ФУНКЦІЇ ВИДУ Y = F(-X)
f(x) => f(-x)
Очевидно, що функції y = f(-x) та y = f(x) приймають рівні значення в точках, абсциси яких рівні за абсолютною величиною, але протилежні за знаком. Інакше висловлюючись, ординати графіка функції y = f(-x) у сфері позитивних (негативних) значень х дорівнюватимуть ординатам графіка функції y = f(x) при відповідних за абсолютною величиною негативних (позитивних) значеннях х. Отже, отримуємо таке правило.
Для побудови графіка функції y = f(-x) слід побудувати графік функції y = f(x) та відобразити його щодо осі ординат. Отриманий графік є графіком функції y = f(-x)
ПОБУДУВАННЯ ГРАФІКА ФУНКЦІЇ ВИДУ Y = - F(X)
f(x) => - f(x)
Ординати графіка функції y = - f(x) при всіх значеннях аргументу дорівнюють абсолютної величини, але протилежні за знаком ординатам графіка функції y = f(x) при тих же значеннях аргументу. Отже, отримуємо таке правило.
Для побудови графіка функції y = f (x) слід побудувати графік функції y = f (x) і відобразити його щодо осі абсцис.
Приклади:
1.y=-f(x)
2.y=f(-x)
3.y=-f(-x)
Деформація.
ДЕФОРМАЦІЯ ГРАФІКА ВДОЛІ ОСІ ОРДИНАТ
f(x) => k f(x)
Розглянемо функцію виду y = k f(x), де k > 0. Неважко помітити, що при рівних значеннях аргументу ординати графіка цієї функції будуть у k разів більшими за ординат графіка функції у = f(x) при k > 1 або 1/k разів менше ординат графіка функції y = f(x) при k Для побудови графіка функції y = k f(x) слід побудувати графік функції y = f(x) і збільшити його ординати в k разів при k > 1(виконати розтягнення графіка вздовж осі ординат ) або зменшити його ординати в 1/k разів при k
k > 1- Розтяг від осі Ох
0 - стиск до осі OX
ДЕФОРМАЦІЯ ГРАФІКА ВДОЛІ ОСІ АБСЦІСС
f(x) => f(k x)
Нехай потрібно побудувати графік функції y = f(kx), де k>0. Розглянемо функцію y = f(x), яка у довільній точці x = x1 набуває значення y1 = f(x1). Очевидно, що функція y = f(kx) приймає таке ж значення в точці x = x2, координата якої визначається рівністю x1 = kx2, причому ця рівність справедлива для сукупності всіх значень х з області визначення функції. Отже, графік функції y = f(kx) виявляється стислим (при k 1) вздовж осі абсцис щодо графіка функції y = f(x). Отже, отримуємо правило.
Для побудови графіка функції y = f(kx) слід побудувати графік функції y = f(x) і зменшити його абсциси в k раз при k>1 (виконати стиснення графіка вздовж осі абсцис) або збільшити його абсциси в 1/k раз при k
k > 1- Стиснення до осі Оу
0 - розтяг від осі OY
§ 11. Графіки синуса та косинуса | ||||||
Повторити: § 5. Годинник, або сучасний поглядна тригонометрію. |
||||||
Побудуємо графік функції y = sin x. При цьому нам знову при- |
||||||
годиться годинник із § 5. | ||||||
Якщо x = 0, то, очевидно, y = 0. Коли x воз- | ||||||
зростає від 0 до π/2, число sin x зростає від 0 до | ||||||
1 (уявіть собі, як змінюється ордината кон- | ||||||
ця стрілки на наших фірмових годинниках). Ділянка | ||||||
графіка для x від 0 до π/2 зображено на рис. 11.1. | ||||||
При малих x наш графік близький до прямої | ||||||
y = x: пригадаємо, що за малих x вірна при- | ||||||
ближня формула sin x ≈ x. Можна сказати, | ||||||
що пряма y = x стосується кривої з рівнянням | ||||||
y = sin x у точці (0; 0). Зауважимо також, що наша ділянка графіка |
||||||
розташований нижче цієї прямої: адже для гострих кутів x, виміряний- |
||||||
них у радіанах, виконано нерівність sin x< x. | ||||||
Чим ближче x до π/2, тим більше порожнього йде наша крива. Це |
||||||
відбувається тому, що проекція кінця стрілки на вісь ординат, |
||||||
вагаючись по відрізку [-1; 1], швидше за все рухається в середині |
||||||
відрізка і сповільнюється біля його країв: ми вже обговорювали в § 5. |
||||||
від ? до 3?/2, sin x зменшується від 0 до -1, а коли x зростає від ? ). Зауважимо, до речі, що крива на рис11.2 а симетрична щодо вертикальної прямої з рівнянням x = π/2. Справді, формула наведення sin(π/2 − x) = sin x показує, що точки з абсцисами x і π − x мають на графіку однакові ординати і, отже, симетричні щодо прямої x = π/2 (рис.11.3) а).
Завдання 11.1. Запишіть рівняння прямої, що стосується графіка функції y = sin x у точці з координатами (π; 0).
Крива на рис 11.2 б центрально симетрична щодо точки з координатами (π; 0); це випливає з іншої формули приведення: sin(2π − x) = − sin x (рис.11.3 б).
Після того, як ми маємо ділянку графіка функції y = sin x для 0 6 x 6 2π, весь графік будується вже просто. Справді, коли кінець стрілки пройшов шлях 2π, стрілка повернулася у вихідне положення; при подальшому русі все повторюватиметься. Отже, графік складатиметься з таких самих шматків, як у рис 11.2 б. Остаточно графік функції y = sin x має такий вигляд, як у рис.11.4 . У цьому ділянки графіка при x , , [−2π; 0]. . . виходять з графіка на рис11.2 б зрушенням уздовж осі абсцис на 2π, 4π, −2π,. . . відповідно. Це просто переформулювання того факту, що функція y = sin x має період 2π.
Мал. 11.4. y = sin x.
Мал. 11.5. y = cos x.
Тепер збудуємо графік функції y = cos x. Можна було б будувати його так, як ми будували графік синуса. Ми, однак, оберемо інший шлях, який дозволить використовувати інформацію, яка вже є у нас.
Саме скористаємося формулою приведення sin(x + π/2) = = cos x. Цю формулу можна розуміти так: функція y = cos x приймає самі значення, як і функція y = sin x, але на π/2 раніше. Наприклад, функція y = sin x приймає значення 1 при x = π/2, а функція y = cos x = sin(x + π/2) приймає це значення вже при x = 0. На графіку це означає наступне: для кожної точки графіка y = sin x є точка графіка y = cos x, у якої ордината та сама, а абсциса на π/2 менше (рис. 11.5). Отже, графік y = cos x вийде, якщо зрушити графік y = sin x уздовж осі абсцис на π/2 вліво. На рис.11.5 графік функції y = cos x зображено суцільною кривою.
Отже, ми з'ясували, що графік косинуса виходить преобра-
ванням (зрушенням) з графіка синуса. Випадки, коли графік однієї функції можна отримати перетворенням із графіка іншої функції, цікаві й самі собою, тому скажемо про них кілька слів.
Як, наприклад, виглядатиме графік функції y = 2 sin x? Зрозуміло, що ординати точок цього графіка виходять з ординат відповідних точок графіка y = sin x множенням на 2, тому наш графік зобразиться суцільною кривою на рис. 11.6. Можна сказати, що графік y = 2 sin x виходить із графіка y = sin x розтягуванням вдвічі вздовж осі ординат.
Мал. 11.6. y = 2 sin x. | |||
Мал. 11.7. y = sin 2x.
Тепер збудуємо графік функції y = sin 2x. Легко зрозуміти,
Мал. 11.8. y = sin(2x + π/3).
що функція y = sin 2x приймає ті самі значення, що і функція y = sin x, але при вдвічі менших значеннях x. Наприклад, функція y = sin x приймає значення 1 при x = π/2, а функція y = sin 2x - вже за x = π/4; іншими словами, щоб отримати графік y = sin 2x, треба абсциси всіх точок графіка y = sin x зменшити вдвічі, а ординати залишити незмінними. Те, що виходить, зображено на рис. 11.7. Можна сміливо сказати, що графік y = sin 2x (суцільна лінія на рис.11.7 ) виходить із графіка y = sin x стисненням вдвічі до осі ординат.
Спробуємо побудувати графік функції y = sin(2x + π/3). Зрозуміло, що він має виходити якимось перетворенням із графіка y = sin 2x. На погляд може здатися, що це перетворення - зрушення вліво на π/3 вздовж осі абсцис, за аналогією з тим, що зображено на рис.11.5. Однак, якби це було так, то вийшло б, наприклад, що функція y = sin(2x + π/3) набуває значення 1 при x = π/4 − π/3 = π/12, що не відповідає дійсності (перевірте !). Правильно міркувати так: sin(2x + π/3) = sin 2(x + π/6), так що функція y = sin(2x+π/3) набуває тих же значень, що і функція y = sin 2x, але на π/6 раніше. Отже зрушення вліво - не так на π/3, але в π/6 (рис.11.8 ).
Криві, що є графіками функцій y = a sin bx, де a 6 = 0, b 6 = 0, називаються синусоїдами. Зауважимо, що кривою "косинусоїда" вводити не треба: як ми бачили, графік косинуса - це та ж крива, що і графік синуса, тільки інакше розташований.
ня щодо осей координат.
Завдання 11.2. Які координати точок, позначені на рис. 11.8 знаками запитання?
Завдання 11.3. Візьміть свічку, тонкий аркуш паперу та гострий ніж. Намотайте аркуш паперу на свічку в кілька шарів і обережно розріжте цю свічку разом з папером навскіс ножем. Тепер розгорніть папір. Ви побачите, що вона виявилася розрізаною хвилястою лінією. Доведіть, що ця хвиляста лінія є синусоїдою.
Завдання 11.4. Побудуйте графіки функцій: | ||||||||||||||
г) y = 3 cos 2x; | ||||||||||||||
а) y = − sin x; б) | в) y = cos(x/2); | |||||||||||||
ж) y = sin(πx). д) | ||||||||||||||
Зауваження. Якщо ви будуєте графіки тригонометричних функційна картатому папері, зручно вибрати трохи різні масштаби по осях, щоб на осі абсцис числу π відповідало ціле число клітин. Наприклад, часто вибирають такий масштаб: по осі ординат відрізок довжини 1 займає дві клітинки, по осі абсцис відрізок довжини π займає 6 клітин.
Завдання 11.5. Побудуйте графіки функцій:
а) y = arcsin x; б) y = arccos x.
Подивимося, як виглядають на графіках вже відомі нам розв'язки рівнянь sin x = a та cos x = a. Ці рішення є абсцисами точок перетину горизонтальної прямої y = a з графіком функцій y = sin x (відповідно y = cos x). На рис. 11.9 ,11.10 добре видно дві серії рішень, що виходять при −1< a < 1.
За графіками синуса і косинуса видно, яких проміжках ці функції зростають, але в яких убувають. Зрозуміло, наприклад, що функція y = sin x зростає відрізках [−π/2; π/2],
Перетворення графіків функцій
У цій статті я познайомлю вас з лінійними перетвореннями графіків функцій і покажу, як за допомогою цих перетворень із графіка функції отримати графік функції 
Лінійним перетворенням функції називається перетворення самої функції та/або її аргументу на вигляд 
, а також перетворення, що містить модуль аргументу та/або функції.
Найбільші труднощі під час побудови графіків з допомогою лінійних перетворень викликають такі действия:
ІСаме на цих моментах ми і зупинимося докладніше.
Розглянемо уважно функцію
У її основі лежить функція. Назвемо її базовою функцією.
При побудові графіка функції ми здійснюємо перетворення графіка базової функції.
Якби ми робили перетворення функції у тому порядку, в якому знаходили її значення при певному значенні аргументу, то
Розглянемо які види лінійних перетворень аргументу та функції існують, та як їх виконувати.
Перетворення аргументу.
1. f(x) f(x+b)
1. Будуємо графік функції
2. Зсуваємо графік функції вздовж осі ОХ на | b | одиниць
Побудуємо графік функції
1. Будуємо графік функції
2. Зрушуємо його на 2 одиниці вправо:
2. f(x) f(kx)
1. Будуємо графік функції
2. Абсциси точок графіка ділимо на к, ординати точок залишаємо без змін.
Побудуємо графік функції.
1. Будуємо графік функції
2. Усі абсциси точок графіка ділимо на 2, ординати залишаємо без змін:
3. f(x) f(-x)
1. Будуємо графік функції
2. Відображаємо його симетрично щодо осі OY.
Побудуємо графік функції.
1. Будуємо графік функції
2. Відображаємо його симетрично щодо осі OY:
4. f(x) f(|x|)
1. Будуємо графік функції
2. Частину графіка, розташовану ліворуч від осі ОY праємо, частину графіка, розташовану правіше від осі ОY Добудовуємо симетрично щодо осі OY:
Графік функції виглядає так:
Побудуємо графік функції
1. Будуємо графік функції (це графік функції, зміщений вздовж осі ОХ на 2 одиниці вліво):
2. Частина графіка, розташовану ліворуч від осі OY (x<0) стираем:
3. Частину графіка, розташовану правіше від осі OY (x>0) добудовуємо симетрично щодо осі OY:
Важливо! Два основні правила перетворення аргументу.
1. Усі перетворення аргументу відбуваються вздовж осі ОХ
2. Усі перетворення аргументу відбуваються "навпаки" і "у зворотному порядку".
Наприклад, функції послідовність перетворень аргументу така:
1. Беремо модуль від х.
2. До модуля х додаємо число 2.
Але побудову графіка ми робили у зворотному порядку:
Спочатку виконали перетворення 2. - змістили графік на 2 одиниці вліво (тобто абсциси крапок зменшили на 2, як би "навпаки")
Потім виконали перетворення f(x) f(|x|).
Коротко послідовність перетворень записується так:
Тепер поговоримо про перетворення функції . Перетворення відбуваються
1. Уздовж осі OY.
2. У тій самій послідовності, в якій виконуються дії.
Ось ці перетворення:
1. f(x)f(x)+D
2. Зміщуємо його вздовж осі OY на | D | одиниць
Побудуємо графік функції
1. Будуємо графік функції
2. Зміщуємо його вздовж осі OY на 2 одиниці вгору:
2. f(x)Af(x)
1. Будуємо графік функції y = f (x)
2. Ординати всіх точок графіка множимо на А, абсцис залишаємо без змін.
Побудуємо графік функції
1. Побудуємо графік функції
2. Ординати всіх точок графіка помножимо на 2:
3. f(x)-f(x)
1. Будуємо графік функції y = f (x)
Побудуємо графік функції.
1. Будуємо графік функції.
2. Відображаємо його симетрично щодо осі ОХ.
4. f(x)|f(x)|
1. Будуємо графік функції y = f (x)
2. Частину графіка, розташовану вище осі ОХ залишаємо без змін, частину графіка, розташовану нижче за осі OX, відображаємо симетрично щодо цієї осі.
Побудуємо графік функції
1. Будуємо графік функції. Він виходить усуненням графіка функції вздовж осі OY на 2 одиниці вниз:
2. Тепер частину графіка, розташовану нижче осі ОХ, відобразимо симетрично щодо цієї осі:
І останнє перетворення, яке, строго кажучи, не можна назвати перетворенням функції, оскільки результат цього перетворення функцією не є:
| y | = f (x)
1. Будуємо графік функції y = f (x)
2. Частину графіка, розташовану нижче осі ОХ стираємо, потім частину графіка, розташовану вище осі ОХ, добудовуємо симетрично щодо цієї осі.
Побудуємо графік рівняння
1. Будуємо графік функції:
2. Частина графіка, розташовану нижче осі ОХ праємо:
3. Частину графіка, розташовану вище за осю ОХ добудовуємо симетрично щодо цієї осі.
І, нарешті, пропоную вам подивитися ВІДЕОУРОК у якому я показую покроковий алгоритм побудови графіка функції
Графік цієї функції виглядає так:
З графіків видно що:
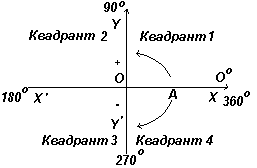На рис. зліва показані перпендикулярні осі ХХ" та YY"; що перетинаються на початку координат О. При роботі з графіками вимірювання вправо і вгору від Про вважаються позитивними, ліворуч і вниз від Про - негативними. Нехай ОА вільно обертається щодо О. При повороті ОА проти годинникової стрілки кут, що вимірюється, вважається позитивним, а при повороті за годинниковою стрілкою - негативним.
Графік. Позитивне чи негативне
напрямок при русі по колу.
Нехай ОА обертається проти годинникової стрілки таким чином, що 1 - будь-який кут у першому квадранті, і побудуємо перпендикуляр АВ для отримання прямокутного трикутника ОАВ на рис. зліва. Оскільки всі три сторони трикутника є позитивними, тригонометричні функції синус, косинус і тангенс у першому квадранті будуть позитивними. (Зазначимо, що довжина ОА завжди є позитивною, оскільки є радіусом кола.)
Нехай ОА обертається далі таким чином, що 2 - будь-який кут у другому квадранті, і побудуємо АС так, щоб утворився прямокутний трикутник ОАС. Тоді sin 2 =+/+ = +; cos Θ 2 =+/- = -; tg 2 =+/- = -. Нехай ОА обертається далі таким чином, що 3 - будь-який кут у третьому квадранті, і побудуємо АD так, щоб утворився прямокутний трикутник ОАD. Тоді sin 3 = -/+ = -; cos 3 = -/+ = -; tg 3 = -/- =+ .
Нехай ОА обертається далі таким чином, що 4 - будь-який кут у четвертому квадранті, і побудуємо АЕ так, щоб утворився прямокутний трикутник ОАЕ. Тоді sin 4 = -/+= -; cos Θ 4 =+/+=+; tg 4 = -/+= -.
У першому квадранті всі тригонометричні функції мають позитивні значення, у другому позитивний тільки синус, у третьому - лише тангенс, у четвертому лише косинус, що й показано на рис. зліва.
Знання кутів довільної величини необхідно при знаходженні, наприклад, всіх кутів між 0 o і 360 o синус яких дорівнює, скажімо, 0,3261. Якщо ввести калькулятор 0,3261 і натиснути кнопку sin -1 , отримаємо відповідь 19,03 o . Однак існує другий кут між 0 o і 360 o який калькулятор не покаже. Синус також позитивний у другому квадранті. Інший кут показано на рис. нижче як кут Θ, де Θ=180 o - 19,03 o = 160,97 o . Таким чином, 19,03 o і 160,97 o - це кути в діапазоні від 0 o до 360 o синус яких дорівнює 0,3261.
Будьте уважні! Калькулятор дає лише одне з цих значень. Друге значення слід визначити згідно з теорією кутів довільної величини.
Приклад 1
Знайти всі кути в діапазоні від 0 o до 360 o , синус яких дорівнює -0,7071 
Рішення:
Кути, синус яких дорівнює -0,7071 o знаходяться в третьому та четвертому квадранті, оскільки синус від'ємний у цих квадрантах (див. рис. зліва).
Графік. Знаходження всіх кутів по
заданому значенню синуса (приклад)
.gif)
Примітка.Калькулятор дає лише одну відповідь.
Графік. Знаходження всіх кутів по
заданому значенню синуса (приклад)
Приклад 2
Знайти всі кути між 0 o і 360 o тангенс яких дорівнює 1, 327. 
Рішення:
Тангенс позитивний у першому та третьому квадрантах - рис. зліва.
Графік. Знаходження всіх кутів по
З рис нижче Θ = arctg1,327 = 53 o. .gif)
Два кути в діапазоні від 0 o до 360 o тангенс яких дорівнює 1327 це 53 o і 180 o + 53 o т.е. 233 o .
Графік. Знаходження всіх кутів по
заданому значенню тангенсу (приклад)
Нехай ОR на рис. ліворуч- це вектор одиничної довжини, що вільно обертається проти годинникової стрілки навколо О. За один оборот виходить коло, показаний на рис. і розділений секторами по 15 o. Кожен радіус має горизонтальну та вертикальну складову. Наприклад, для 30 o вертикальна складова - це TS, а горизонтальна - OS. З визначення тригонометричних функцій
sin30 o = TS/TO = TS/1, тобто. TS = sin30 oі cos30 o = OS / TO = OS / 1, тобто. OS=cos30 o
Вертикальну складову TS можна перенести на графік у вигляді T"S", що дорівнює значенню, що відповідає куту 30 o на графіку залежності y від кута х. Якщо всі вертикальні складові, подібно до TS, перенести на графік, то вийде синусоїда, показана на рис. вище.
 |
 |
 |
 |
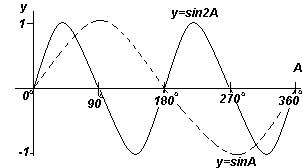Періодичні функції та період
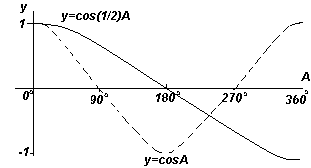
Кожен із графіків функцій, показаних на чотирьох рис. вище, повторюється зі збільшенням кута А, тому їх називають періодичними функціями.
Функції y=sinA та y=cosA повторюються через кожні 360 o (або 2π радіан), тому 360 o називається періодомцих функцій. Функції y = sin2A і y = cos2A повторюються через кожні 180 o (або π радіан), тому 180 o - це період для даних функцій.
У випадку якщо y=sinpA і y=cospA (де р - константа), то період функції дорівнює 360 o /p (або 2π/p радіан). Отже, якщо y=sin3A, то період цієї функції дорівнює 360 o /3= 120 o якщо y=cos4A, то період цієї функції дорівнює 360 o /4= 90 o .
Амплітуда
Амплітудоюназивається максимальне значення синусоїди. Кожен із графіків 1-4 має амплітуду +1 (тобто вони коливаються між +1 та -1). Однак, якщо y=4sinA, кожна з величин sinA множиться на 4, таким чином, максимальна величина амплітуди - 4. Аналогічно для y=5cos2A амплітуда дорівнює 5, а період - 360 o /2 = 180 o .
приклад 3.
Побудувати y=3sin2A у діапазоні від А= 0 o до А=360 o . 
Рішення:
Амплітуда = 3, період = 360 o /2 = 180 o.
приклад 4.
Побудувати графік y=4cos2x у діапазоні від х=0 o до х=360 o 
Рішення:
Амплітуда = 4. період = 360 o /2 = 180 o.
Кути запізнення та випередження
Криві синуса та косинуса не завжди починаються в 0 o . Щоб врахувати цю обставину, періодична функція представляється у вигляді y=sin(A±α), де α - зсув фази щодо y=sinA та y=cosA.
.gif)
Склавши таблицю значень, можна побудувати графік функції y = sin (A-60 o), показаний на рис. зліва. Якщо крива y=sinA починається в 0 o , то крива y=sin(A-60 o) починається в 60 o (тобто її нульове значення на 60 o правіше). Таким чином, кажуть, що y=sin(A-60 o) запізнюєтьсящодо y=sinA на 60 o .
Графік. y=sin(A-60 o) (синусоїда).
.gif)
Склавши таблицю значень, можна побудувати графік функції y = cos (A + 45 o), показаний на рис. нижче.
Якщо крива y=cosA починається в 0 o , то крива y=cos(A+45 o) починається на 45 o ліворуч (тобто її нульова величина знаходиться на 45 o раніше).
Таким чином, кажуть, що графік y = cos (A + 45 o) випереджаєграфік y=cosA на 45 o .
Графік. y=cos(A+45 o) (косинусоїда).
Загалом, графік y=sin(A-α) запізнюється щодо y=sinAна кут α.
Косинусоїда має ту форму, як і синусоїда, але починається на 90 o ліворуч, тобто. випереджає її на 90 o. Отже, cosA=sin(A+90 o).
Приклад 5.
Побудувати графік y=5sin(A+30 o) у діапазоні від А=0 o до А=360 o
.gif)
Приклад 6.
Побудувати графік y=7sin(2A-π/3) в діапазоні від А=0 до А=360 o .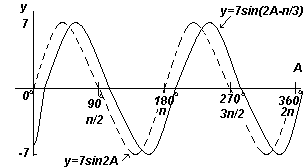 
Рішення:
Амплітуда = 7, період = 2π/2 = π радіан
У загальному випадку y=sin(pt-α) запізнюється щодо y=sinpt на α/p, Отже 7sin(2A-π/3) запізнюється щодо 7sin2A на (π/3)/2, тобто. на π/6 радіан або на 30 o
Синусоїда виду Asin(ωt±α). Фазовий кут. Зсув фазою. 
Нехай OR на рис. ліворуч являє собою вектор, що вільно обертається проти годинникової стрілки навколо Про зі швидкістю радіан/с. Вектор, що обертається, називається фазовим вектором. Через час t секунд OR повернеться на кут t радіан (на рис. зліва це кут TOR). Якщо перпендикулярно OR побудувати ST, то sinωt=ST/OT, тобто. ST=OTsinωt.
Якщо всі подібні вертикальні складові спроектувати на графік залежності від ωt, вийде синусоїда з амплітудою OR.
Якщо фазовий вектор OR робить один оборот (тобто 2π радіан) за Т секунд, то кутова швидкість ω=2π/Т рад/с, звідки
Т=2π/ ω (с), де
Т – це період
Число повних періодів, що проходять за 1 секунду, називається частотою f.
Частота = (кількість періодів)/(секунда) = 1/ T = ω/2π Гц,тобто. f= ω/2π Гц
Отже, кутова швидкість
ω=2πf рад/с.
Якщо у загальному вигляді синусоїдальна функція виглядає як y=sin(ωt± α), то
А – амплітуда
ω - кутова швидкість
2π/ ω - період Т, с
ω/2π - частота f, Гц
α - кут випередження або запізнення (щодо y=Аsinωt) у радіанах, він називається також фазовим кутом.
Приклад 7.
Змінний струм визначається як i=20sin(90πt+0,26) ампер. Визначити амплітуду, період, частоту та фазовий кут (у градусах)
Рішення:
i=20sin(90πt+0,26)А, отже,
амплітуда дорівнює 20 А
кутова швидкість ω=90π, отже,
період Т= 2π/ω = 2π/ 90π = 0,022 с = 22мс
частота f= 1/Т = 1/0,022 = 45,46 Гц
фазовий кут α= 0,26 рад. = (0,26 * 180/π) o = 14,9 o.
приклад 8.
Коливальний механізм має максимальне усунення 3 м і частоту 55 Гц. Під час t=0 усунення становить 100см. Виразити усунення у загальному вигляді Аsin(ωt± α).
Рішення
Амплітуда = максимальне усунення = 3м
Кутова швидкість ω=2πf = 2π(55) = 110 πрад./с
Отже, усунення 3sin(110πt + α) м.
При t=0 усунення = 100см=1м.
Отже, 1=3sin(0 + α), тобто. sinα=1/3=0,33
Отже α=arcsin0,33=19 o
Отже, зсув дорівнює 3sin(110 πt + 0,33).
Приклад 9.
Значення миттєвого напруження у схемі змінного струму у будь-які t секунд задається у вигляді v=350sin(40πt-0,542)В. Знайти:
а) Амплітуду, період, частоту та фазовий кут (у градусах)
б) значення напруги за t =0
в) значення напруги при t = 10 мс
г) час, протягом якого напруга вперше досягне значення 200 У. 
Рішення:
а) Амплітуда дорівнює 350 В, кутова швидкість дорівнює ω=40π
Отже,
період Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовий кут = 0,542 рад (0,542*180/π) = 31 o із запізненням щодо v=350sin(40πt)
б) Якщо t =0, то v=350sin(0-0,542)=350sin(-31 o)=-180,25
в) Якщо t =10 мс, то v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6
г) Якщо v=200 І, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)
Графік. Коливальний механізм
(Приклад, синусоїда).
v=350sin(40πt-0,542) Отже, (40πt-0,542)=arcsin200/350=35 o або 0,611 рад.
40πt = 0,611 +0,542 = 1,153.
Отже, якщо v=200В, час t=1,153/40π=9,179 мс
