
Electric field energy. The energy of a charged capacitor can be expressed in terms of quantities characterizing electric field in the gap between the plates. Let's do this using the example of a flat capacitor. Substituting the expression for capacitance into the formula for the energy of a capacitor gives
Private U / d equal to the field strength in the gap; work S· d is the volume V occupied by the field. Consequently,
![]()
If the field is uniform (which is the case in a flat capacitor at a distance d much smaller than the linear dimensions of the plates), then the energy contained in it is distributed in space with a constant density w. Then bulk energy density electric field is
Taking into account the relation, we can write
In an isotropic dielectric, the directions of the vectors D and E match and
We substitute the expression , we get
The first term in this expression coincides with the energy density of the field in vacuum. The second term is the energy spent on the polarization of the dielectric. Let us show this by the example of a nonpolar dielectric. The polarization of a nonpolar dielectric is that the charges that make up the molecules are displaced from their positions under the influence of an electric field E. Per unit volume of the dielectric, the work expended on the displacement of charges q i by d r i , is
The expression in brackets is the dipole moment per unit volume or the polarization of the dielectric R. Consequently, .
Vector P linked to vector E ratio . Substituting this expression into the formula for work, we get
Having carried out the integration, we determine the work expended on the polarization of a unit volume of the dielectric
Knowing the energy density of the field at each point, you can find the energy of the field enclosed in any volume V. To do this, you need to calculate the integral:
QUESTION
electricity- directed (ordered) movement of charged particles. Such particles can be: in metals - electrons, in electrolytes - ions (cations and anions), in gases - ions and electrons, in vacuum under certain conditions - electrons, in semiconductors - electrons and holes (electron-hole conductivity). Sometimes electric current is also called the displacement current resulting from a change in time electric field.
Electric current has the following manifestations:
heating of conductors (in superconductors there is no heat release);
· change chemical composition conductors (observed mainly in electrolytes);
· creation magnetic field(manifested in all conductors without exception).
If charged particles move inside macroscopic bodies relative to a particular medium, then such a current is called an electric conduction current. If macroscopic charged bodies are moving (for example, charged raindrops), then this current is called convection current.
Distinguish between a variable alternating current, AC), permanent (eng. direct current, DC) and pulsating electric currents, as well as their various combinations. In such terms, the word "electric" is often omitted.
Direct current - current, the direction and magnitude of which change little over time.
Alternating current is a current whose magnitude and direction change with time. AT broad sense Alternating current is any current that is not direct. Among the alternating currents, the main one is the current, the value of which varies according to a sinusoidal law. In this case, the potential of each end of the conductor changes with respect to the potential of the other end of the conductor alternately from positive to negative and vice versa, while passing through all intermediate potentials (including the zero potential). As a result, a current arises that continuously changes direction: when moving in one direction, it increases, reaching a maximum, called the amplitude value, then decreases, at some point becomes zero, then increases again, but in the other direction and also reaches the maximum value , falls off to then pass through zero again, after which the cycle of all changes resumes.
Quasi-stationary current- “a relatively slowly changing alternating current, for the instantaneous values of which the laws of direct currents are satisfied with sufficient accuracy” (TSB). These laws are Ohm's law, Kirchhoff's rules and others. Quasi-stationary current, as well as direct current, has the same current strength in all sections of an unbranched circuit. When calculating quasi-stationary current circuits due to the emerging e. d.s. capacitance and inductance inductions are taken into account as lumped parameters. Quasi-stationary are ordinary industrial currents, except for currents in long-distance transmission lines, in which the condition of quasi-stationarity along the line is not satisfied.
High frequency alternating current- current, in which the condition of quasi-stationarity is no longer satisfied, the current passes over the surface of the conductor, flowing around it from all sides. This effect is called the skin effect.
Pulsating current is a current in which only the magnitude changes, but the direction remains constant.
Eddy currents[edit | edit source text]
Main article:Eddy currents
Eddy currents (Foucault currents) are “closed electric currents in a massive conductor that occur when the magnetic flux penetrating it changes”, therefore eddy currents are induction currents. The faster the magnetic flux changes, the stronger the eddy currents. Eddy currents do not flow along certain paths in the wires, but, closing in the conductor, form vortex-like contours.
The existence of eddy currents leads to the skin effect, that is, to the fact that the alternating electric current and magnetic flux propagate mainly in the surface layer of the conductor. Heating by eddy currents of conductors leads to energy losses, especially in the cores of the coils alternating current. To reduce energy losses due to eddy currents, the alternating current magnetic circuits are divided into separate plates, isolated from each other and located perpendicular to the direction of eddy currents, which limits the possible contours of their paths and greatly reduces the magnitude of these currents. At very high frequencies, instead of ferromagnets, magnetodielectrics are used for magnetic circuits, in which, due to the very high resistance, eddy currents practically do not occur.
Characteristics[edit | edit source]
Historically, it is accepted that the direction of the current coincides with the direction of movement of positive charges in the conductor. In this case, if the only current carriers are negatively charged particles (for example, electrons in a metal), then the direction of the current is opposite to the direction of movement of charged particles. .
The speed of the directed motion of particles in conductors depends on the material of the conductor, the mass and charge of the particles, the ambient temperature, the applied potential difference, and is much less than the speed of light. In 1 second, the electrons in the conductor move by orderly movement by less than 0.1 mm. Despite this, the rate of propagation of the actual electric current equal to the speed of light (speed of propagation of the front of an electromagnetic wave). That is, the place where the electrons change their speed of movement after a change in voltage moves with the speed of propagation electromagnetic oscillations.
Strength and current density[edit | edit source]
Main article:Current strength
Electric current has quantitative characteristics: scalar - current strength, and vector - current density.
The current strength is a physical quantity equal to the ratio of the amount of charge that has passed through the cross section of the conductor in some time to the value of this time interval.
Current in international system units (SI) is measured in amperes ( Russian designation: AND).
According to Ohm's law, the current strength in a circuit section is directly proportional to the voltage applied to this section of the circuit, and inversely proportional to its resistance:
If the electric current is not constant in the circuit section, then the voltage and current strength are constantly changing, while for ordinary alternating current the average values of voltage and current strength are zero. However, the average power of the heat released in this case is not equal to zero. Therefore, the following terms are used:
instantaneous voltage and current, that is, acting at a given moment in time.
amplitude voltage and current strength, that is, the maximum absolute values
The effective (effective) voltage and current strength are determined by the thermal effect of the current, that is, they have the same values that they have for direct current with the same thermal effect.
The current density is a vector, the absolute value of which is equal to the ratio of the current flowing through a certain section of the conductor, perpendicular to the direction of the current, to the area of this section, and the direction of the vector coincides with the direction of movement of the positive charges that form the current.
According to Ohm's law in differential form, the current density in the medium is proportional to the electric field strength and the conductivity of the medium:
Power[edit | edit source]
Main article:Joule-Lenz law
In the presence of current in the conductor, work is done against the forces of resistance. The electrical resistance of any conductor consists of two components:
active resistance - resistance to heat generation;
reactance - "resistance due to the transfer of energy to an electric or magnetic field (and vice versa)" (TSB).
Generally, most of the work done by an electric current is released as heat. The power of heat loss is a value equal to the amount of heat released per unit time. According to the Joule-Lenz law, the power of heat loss in a conductor is proportional to the strength of the flowing current and the applied voltage:
Power is measured in watts.
In a continuous medium, the volumetric power loss is determined by the scalar product of the current density vector and the electric field strength vector at a given point:
Volumetric power is measured in watts per cubic meter.
Radiation resistance is caused by the formation of electromagnetic waves around the conductor. This resistance is in complex dependence on the shape and dimensions of the conductor, on the wavelength of the emitted wave. For single straight conductor, in which everywhere the current is of the same direction and strength, and the length of which L is much less than the length of the electromagnetic wave emitted by it, the dependence of the resistance on the wavelength and conductor is relatively simple:
The most used electric current with a standard frequency of 50 Hz corresponds to a wave with a length of about 6 thousand kilometers, which is why the radiation power is usually negligibly small compared to the heat loss power. However, as the frequency of the current increases, the length of the emitted wave decreases, and the radiation power increases accordingly. A conductor capable of radiating appreciable energy is called an antenna.
Frequency[edit | edit source]
See also: Frequency
Frequency refers to an alternating current that periodically changes strength and/or direction. This also includes the most commonly used current, which varies according to a sinusoidal law.
An alternating current period is the shortest period of time (expressed in seconds) after which changes in current (and voltage) are repeated. The number of periods completed by the current per unit of time is called the frequency. Frequency is measured in hertz, one hertz (Hz) corresponds to one cycle per second.
Bias current[edit | edit source]
Main article:Displacement current (electrodynamics)
Sometimes, for convenience, the concept of displacement current is introduced. In Maxwell's equations, the displacement current is present on an equal footing with the current caused by the movement of charges. The intensity of the magnetic field depends on the total electric current, equal to the sum conduction current and displacement current. By definition, the displacement current density is a vector quantity proportional to the rate of change of the electric field over time:
The fact is that when the electric field changes, as well as when the current flows, a magnetic field is generated, which makes these two processes similar to each other. In addition, a change in the electric field is usually accompanied by energy transfer. For example, when charging and discharging a capacitor, despite the fact that there is no movement of charged particles between its plates, they speak of a displacement current flowing through it, carrying some energy and closing the electrical circuit in a peculiar way. The displacement current in the capacitor is determined by the formula:
![]() ,
,
where is the charge on the capacitor plates, is the potential difference between the plates, is the capacitance of the capacitor.
Displacement current is not an electric current, because it is not related to the movement of an electric charge.
Main types of conductors[edit | edit source]
Unlike dielectrics, conductors have free carriers of uncompensated charges, which, under the action of a force, as a rule, the difference electrical potentials, start moving and create an electric current. The current-voltage characteristic (current versus voltage) is the most important characteristic conductor. For metallic conductors and electrolytes, it has simplest form: current is directly proportional to voltage (ohm's law).
Metals - here the current carriers are conduction electrons, which are usually considered as an electron gas, clearly showing the quantum properties of a degenerate gas.
Plasma is an ionized gas. Electric charge is carried by ions (positive and negative) and free electrons, which are formed under the influence of radiation (ultraviolet, X-ray and others) and (or) heating.
Electrolytes - "liquid or solids and systems in which ions are present in any noticeable concentration, causing the passage of an electric current. Ions are formed in the process electrolytic dissociation. When heated, the resistance of electrolytes decreases due to an increase in the number of molecules decomposed into ions. As a result of the passage of current through the electrolyte, the ions approach the electrodes and are neutralized, settling on them. Faraday's laws of electrolysis determine the mass of the substance released on the electrodes.
There is also an electric current of electrons in a vacuum, which is used in cathode ray devices.
Electric currents in nature[edit | edit source]
Intracloud lightning over Toulouse, France. 2006
Atmospheric electricity is electricity that is contained in the air. For the first time, Benjamin Franklin showed the presence of electricity in the air and explained the cause of thunder and lightning. Later it was found that electricity accumulates in the condensation of vapors in upper layers atmosphere, and the following laws are indicated, which atmospheric electricity follows:
In a clear sky, as well as in a cloudy one, the electricity of the atmosphere is always positive, if at some distance from the place of observation it does not rain, hail or snow;
the voltage of the electricity of the clouds becomes strong enough to release it from environment only when cloud vapors condense into raindrops, as evidenced by the fact that there are no lightning discharges without rain, snow or hail at the place of observation, excluding the return stroke of lightning;
Atmospheric electricity increases with increasing humidity and reaches a maximum when rain, hail and snow fall;
· A place where it rains is a reservoir of positive electricity, surrounded by a belt of negative electricity, which, in turn, is enclosed in a belt of positive electricity. At the boundaries of these belts, the stress is zero. The movement of ions under the action of electric field forces forms a vertical conduction current in the atmosphere with medium density, equal to about (2÷3) 10 −12 A/m².
The total current flowing to the entire surface of the Earth is approximately 1800 A.
Lightning is a natural sparking electrical discharge. The electrical nature of the auroras was established. St. Elmo's fires are a natural corona electrical discharge.
Biocurrents - the movement of ions and electrons plays a very significant role in all life processes. The biopotential created in this case exists both at the intracellular level and in separate parts body and organs. The transmission of nerve impulses occurs with the help of electrochemical signals. Some animals ( electric ramps, electric eel) are capable of accumulating a potential of several hundred volts and use this for self-defense.
Application[edit | edit source]
When studying electric current, many of its properties were discovered, which allowed him to find practical use in various areas human activity, and even create new areas that would be impossible without the existence of an electric current. After the electric current found practical application, and for the reason that the electric current can be obtained different ways, in the industrial sphere a new concept arose - the electric power industry.
Electric current is used as a carrier of signals of varying complexity and types in different areas (telephone, radio, control panel, button door lock and so on).
In some cases, unwanted electric currents appear, such as stray currents or short circuit current.
The use of electric current as a carrier of energy[edit | edit source]
obtaining mechanical energy in various electric motors,
obtaining thermal energy in heating appliances, electric furnaces, electric welding,
obtaining light energy in lighting and signaling devices,
excitation of electromagnetic oscillations of high frequency, ultrahigh frequency and radio waves,
receive sound,
receiving various substances through electrolysis. This is where electromagnetic energy is converted into chemical energy.
creation of a magnetic field (in electromagnets).
The use of electric current in medicine[edit | edit source]
Diagnosis - the biocurrents of healthy and diseased organs are different, while it is possible to determine the disease, its causes and prescribe treatment. The section of physiology that studies electrical phenomena in the body is called electrophysiology.
· Electroencephalography - a method of studying the functional state of the brain.
· Electrocardiography - a technique for recording and studying electric fields during the work of the heart.
· Electrogastrography - a method of studying the motor activity of the stomach.
· Electromyography - a method of studying the bioelectric potentials that occur in skeletal muscles.
· Treatment and resuscitation: electrical stimulation of certain areas of the brain; treatment of Parkinson's disease and epilepsy, also for electrophoresis. A pacemaker that stimulates the heart muscle with a pulsed current is used for bradycardia and other cardiac arrhythmias.
QUESTION
Electricity. Current strength.
Ohm's law for a circuit section. conductor resistance.
Series and parallel connection of conductors.
Electromotive force. Ohm's law for a complete circuit.
Work and current power.
Directional movement of electric charges is called electric shock. Electrons can move freely in metals, ions in conducting solutions, and both electrons and ions can exist in a mobile state in gases.
Conventionally, the direction of movement of positive particles is considered to be the direction of current, the current goes from (+) to (-), therefore, in metals this direction is opposite to the direction of movement of electrons.
Current strength I is the amount of charge passing per unit time through the full cross section of the conductor. If a charge q passes through the total cross section of the conductor in time t, then
The unit of current strength is Ampere. If the state of the conductor (its temperature, etc.) is stable, then there is a connection between the voltage applied to its ends and the current that arises in this case. It is called Ohm's law and written like this:
R- electrical resistance conductor, depending on the type of substance and on its geometric dimensions. A conductor has unit resistance, in which a current of 1 A occurs at a voltage of 1 V. This unit of resistance is called an ohm.
Distinguish consistent
and parallel conductor connections.
At serial connection the current flowing through all sections of the circuit is the same, and the voltage at the ends of the circuit is equal to the sum of the voltages in all sections.
The total resistance is equal to the sum of the resistances
At parallel connection conductors, the voltage remains constant, and the current is the sum of the currents flowing through all branches.
In this case, the reciprocal of the resistance are added:
1/R= 1/R 1 +1/R 2 or you can write it like this
To obtain direct current on charges in electrical circuit inside the current source, forces must act that are different from the forces electrostatic field; they are called outside forces.
If we consider complete electrical circuit, it is necessary to include in it the action of these third-party forces and internal resistance current source r. In this case Ohm's law for a complete circuit will take the form:
E - electromotive force(EMF) source. It is measured in the same units as voltage.
The quantity (R + r) is sometimes called circuit impedance.
Let's formulate Kirkhoff's rules:
First rule: the algebraic sum of the strengths of the currents in the sections of the circuit converging at one branching point is equal to zero.
Second rule: for any closed circuit, the sum of all voltage drops is equal to the sum of all EMF in this circuit.
The current power is calculated by the formula
P=UI=I 2 R=U 2 /R.
Joule-Lenz law. The work of electric current ( thermal effect current)
A=Q=UIt=I 2 Rt=U 2 t/R.
QUESTION
A magnetic field- a force field acting on moving electric charges and on bodies with a magnetic moment, regardless of the state of their movement; magnetic component electromagnetic field.
The magnetic field can be created by the current of charged particles and/or by the magnetic moments of electrons in atoms (and by the magnetic moments of other particles, although to a much lesser extent) (permanent magnets).
In addition, it appears in the presence of a time-varying electric field.
The main power characteristic of the magnetic field is magnetic induction vector
(magnetic field induction vector) . From a mathematical point of view ![]() - vector field that defines and specifies the physical concept of a magnetic field. Often the vector of magnetic induction is called simply a magnetic field for brevity (although this is probably not the most strict use of the term).
- vector field that defines and specifies the physical concept of a magnetic field. Often the vector of magnetic induction is called simply a magnetic field for brevity (although this is probably not the most strict use of the term).
Another fundamental characteristic of the magnetic field (alternative magnetic induction and closely related to it, practically equal to it in physical value) is vector potential .
Often in the literature, as the main characteristic of the magnetic field in vacuum (that is, in the absence of a magnetic medium), they choose not the magnetic induction vector, but the magnetic field strength vector, which formally can be done, since these two vectors coincide in vacuum; however, in a magnetic medium, the vector does not carry the same physical sense, being an important, but still auxiliary quantity. Therefore, with the formal equivalence of both approaches for vacuum, from a systematic point of view, it should be considered the main characteristic of the magnetic field precisely
A magnetic field can be called a special kind of matter, through which interaction is carried out between moving charged particles or bodies that have a magnetic moment.
Magnetic fields are a necessary (in the context of special relativity) consequence of the existence of electric fields.
Together, the magnetic and electric fields form the electromagnetic field, the manifestations of which are, in particular, light and all other electromagnetic waves.
Electric current (I), passing through the conductor, creates a magnetic field (B) around the conductor.
From the point of view of quantum field theory, magnetic interaction - as a special case of electromagnetic interaction - is carried by a fundamental massless boson - a photon (a particle that can be represented as a quantum excitation of an electromagnetic field), often (for example, in all cases of static fields) - virtual.
Sources of the magnetic field[edit | edit source]
The magnetic field is created (generated) by the current of charged particles, or by a time-varying electric field, or by the intrinsic magnetic moments of the particles (the latter, for the sake of uniformity of the picture, can be formally reduced to electric currents).
Calculation[edit | edit source]
In simple cases, the magnetic field of a current-carrying conductor (including the case of a current distributed arbitrarily over volume or space) can be found from the Biot-Savart-Laplace law or the circulation theorem (it is also Ampère's law). In principle, this method is limited to the case (approximation) of magnetostatics - that is, the case of constant (if we are talking about strict applicability) or rather slowly changing (if we are talking about approximate application) magnetic and electric fields.
In more difficult situations is sought as a solution to Maxwell's equations.
The manifestation of the magnetic field[edit | edit source]
The magnetic field manifests itself in the effect on the magnetic moments of particles and bodies, on moving charged particles (or current-carrying conductors). The force acting on an electrically charged particle moving in a magnetic field is called the Lorentz force, which is always directed perpendicular to the vectors v and B. It is proportional to the charge of the particle q, the velocity component v, perpendicular to the direction of the magnetic field vector B, and the magnitude of the magnetic field induction B. In the SI system of units, the Lorentz force is expressed as follows:
![]()
in system cgs units:
![]()
where square brackets denote the vector product.
Also (due to the action of the Lorentz force on charged particles moving along the conductor), the magnetic field acts on the conductor with current. The force acting on a current-carrying conductor is called the ampere force. This force is the sum of the forces acting on individual charges moving inside the conductor.
Interaction of two magnets[edit | edit source]
One of the most common manifestations of a magnetic field in ordinary life is the interaction of two magnets: identical poles repel, opposite ones attract. It seems tempting to describe the interaction between magnets as an interaction between two monopoles, and from a formal point of view, this idea is quite realizable and often very convenient, and therefore practically useful (in calculations); however, a detailed analysis shows that in fact this is not completely correct description phenomenon (the most obvious question that cannot be explained within the framework of such a model is the question of why the monopoles can never be separated, that is, why the experiment shows that no isolated body actually has a magnetic charge; in addition, the weakness of the model is that it is inapplicable to a magnetic field created by a macroscopic current, and therefore, if not considered as a purely formal technique, it only leads to a complication of the theory in a fundamental sense).
It would be more correct to say that a force acts on a magnetic dipole placed in an inhomogeneous field, which tends to rotate it so that the magnetic moment of the dipole is co-directed with the magnetic field. But no magnet experiences a (total) force from a uniform magnetic field. Force acting on a magnetic dipole with a magnetic moment m is expressed by the formula:
The force acting on a magnet (not being a single point dipole) from an inhomogeneous magnetic field can be determined by summing all the forces (defined by this formula) acting on the elementary dipoles that make up the magnet.
However, an approach is possible that reduces the interaction of magnets to the Ampère force, and the formula itself above for the force acting on a magnetic dipole can also be obtained based on the Ampère force.
Phenomenon electromagnetic induction[edit | edit source]
Main article:Electromagnetic induction
If the flow of the magnetic induction vector through a closed circuit changes in time, an electromagnetic induction emf arises in this circuit, generated (in the case of a fixed circuit) by a vortex electric field arising from a change in the magnetic field with time (in the case of a magnetic field unchanged with time and a change in the flux from - due to the movement of the conductor circuit, such an EMF arises through the action of the Lorentz force).
QUESTION
acon of Biot-Savart-Laplace- a physical law for determining the induction vector of a magnetic field generated by a direct electric current. It was established experimentally in 1820 by Biot and Savart and formulated in general view Laplace. Laplace also showed that this law can be used to calculate the magnetic field of a moving point charge (assuming the movement of one charged particle is a current).
The Biot-Savart-Laplace law plays the same role in magnetostatics as Coulomb's law plays in electrostatics. The Biot-Savart-Laplace law can be considered the main law of magnetostatics, deriving from it the rest of its results.
In the modern formulation, the Biot-Savart-Laplace law is more often considered as a consequence of two Maxwell equations for a magnetic field under the condition of a constant electric field, i.e. in the modern formulation, Maxwell's equations act as more fundamental (primarily, if only because the Biot-Savart-Laplace formula cannot simply be generalized to the general case of time-dependent fields).
For a current flowing along a circuit (thin conductor)[edit | edit source]
Let a direct current flow through a circuit (conductor) located in a vacuum - the point at which the field is sought (observed), then the magnetic field induction in e that point expressed as an integral (in the International System of Units (SI))
where square brackets denote the vector product, - the position of the contour points, - the vector of the contour element (the current flows along it); - magnetic constant; - unit vector directed from the contour element to the observation point.
Theme: Electric field energy
1. Energy of a solitary charged conductor
and systems of charged conductors
![]()
2. Energy of a charged capacitor
![]()
4. Ponderomotive forces. Application of the law of conservation of energy to the calculation of ponderomotive forces.
Energy of a solitary charged conductor and a system of conductors
When a conductor is given a certain charge, an electric field arises around it. To inform the conductor of the next portion of the charge, it is necessary to do work against the forces of this field. Since the electrostatic field is potential, the work done goes to increase the potential energy of the conductor.
Consider a solitary conductor with a capacitance FROM and potential . When transferring charge dQ from infinity to the surface of the conductor, it is necessary to do work dA against the forces of the field
Both quantities on the right side of formula (1) are variables. Using the relationship between quantities FROM, and Q let's bring the right part to one variable. For this, we express dQ through and substitute into formula (1)
To find the work of charging a conductor from zero potential to some potential let's integrate the expression (2)
 .(3)
.(3)
By definition, this work is equal to the change in potential energy. therefore solitary conductor energy, charged to the potential is determined by the formula
Using the relationship between quantities FROM, and Q formula (4) can be represented in several forms
Applying the principle of superposition of electric fields, one can obtain the following formula for the energy of the system from n motionless charged conductors
where is the potential of the total field at the point where the conductor with the charge is located Q i .
Energy of a charged capacitor
The process of charging a capacitor can be represented as a sequential movement of small portions dQ charge from one plate (plate) to another. If the plates are initially neutral, then the transfer of, for example, a positive charge from the first plate to the second will lead to the appearance of a negative charge on the first plate. Consequently, as a result of such transfers, the first plate will be charged negatively, and the second - positively. Between the plates there will be a gradually increasing potential difference 1 – 2 =U. The derivation of the formula for the energy of a charged capacitor is similar to the derivation of formula (4) above. The difference lies in the replacement of the potential for potential difference U
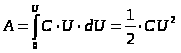 .
(7)
.
(7)
So the formula for charged capacitor energy It has next view
3. Energy of the electrostatic field. Volumetric energy density.
When studying the field stationary charges we cannot consider separately the electric charge and the electric field created by it. Therefore, remaining within the framework of electrostatics, it is impossible to unambiguously indicate whether the carrier of electrical energy is an electric charge or an electric field. The study of variable electromagnetic fields showed that they can exist separately from the electric charges that gave rise to them and propagate in space in the form of electromagnetic waves. The fact of the existence of electromagnetic waves and the transfer of energy by them allows us to assert that the energy of charged conductors is concentrated in an electric field. Taking this into account, we transform formula (7) for the energy of a charged capacitor in such a way that it includes the field characteristic - its strength. For this, in (7) instead of the capacity FROM we substitute the expression for the capacitance of a flat capacitor, and the voltage U replace with the expression . Then for the energy of a charged capacitor we get
![]() . (9)
. (9)
The product in formula (9) is equal to the volume V occupied by the electric field. Dividing the left and right parts of formula (9) by the volume V we get the formula for volume energy density w(energy per unit volume)
![]() or . (10)
or . (10)
Considering the electrical displacement connection D with polarization R dielectric ![]() , we can obtain another formula for the volume energy density of the electric field
, we can obtain another formula for the volume energy density of the electric field
![]() .
(11)
.
(11)
In formula (11), the first term expresses the energy density of the electric field in vacuum, and the second term expresses the energy spent on the polarization of a unit volume of the dielectric.
In the general case of an inhomogeneous electric field, its energy in a certain volume V can be calculated using the formula
4. Ponderomotive forces. Application of the law of conservation of energy to the calculation of ponderomotive forces.
A mechanical force acts on any charged body placed in an electric field. Ponderomotive forces are forces acting from the electric field on macroscopic charged bodies..
Let us determine the force of mutual attraction between oppositely charged plates of a flat capacitor (ponderomotive force) in two ways.
On the one hand, this force can be defined as the force F 2 acting on the second plate from the side of the first
where Q 2 is the amount of charge on the second plate, E 1 is the field strength of the first plate.
Charge amount Q 2 the second plate is determined by the formula
where σ 2 is the surface charge density on the second plate, and the intensity E 1 the field created by the first plate is calculated by the formula
where σ 1 is the surface charge density on the first plate.
We substitute formulas (16) and (15) into formula (14)
![]() or
or 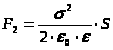 (17) because σ
1
=
σ
2
.
(17) because σ
1
=
σ
2
.
Given that ![]() , we obtain the formula for the force acting on one plate from the other
, we obtain the formula for the force acting on one plate from the other
![]() .
.
For the force acting per unit area of the plate, the formula will have the following form
Now we get the formula for the ponderomotive force using the law of conservation of energy. If a body moves in an electric field, then the ponderomotive forces of the field will do work AND. According to the law of conservation of energy, this work will be done due to the energy of the field, that is
Or . (nineteen)
The work of changing the distance between the plates of a charged capacitor by the value dx is determined by the formula
where F is the force of interaction between the plates (ponderomotive force).
The energy of a charged capacitor is determined by formula (9). When one of the plates is displaced by a distance dx energy of the capacitor will change by the value
![]() (21).
(21).
Equating formulas (20) and (21), we obtain the formula for the force acting per unit area of the plate
As you can see, formulas (18) and (22) are the same. At the same time, the use of the law of conservation of energy to calculate ponderomotive forces greatly simplifies the calculations.
Questions for self-examination:
1. Derive a formula for the energy of a solitary charged conductor and a system of conductors.
2. What is the carrier of electrical energy? What is meant by volumetric energy density? Derive a formula for the volumetric energy density of the electric field.
3. What is meant by ponderomotive forces? How can we calculate the interaction force between the plates of a charged capacitor?
G Signature of the teacher Dielectrics in electric field, energy electric fields. Electrical field- one of the components of the electromagnetic fields, special kind matter...
WE - bulk density energy electric fields equal to (5) wH - bulk density energy magnetic fields equal to (6) Using...
burning rate; Transformation in the volume of the flame energy electric fields into heat, resulting in increased ... flame spread electric field is affected simultaneously both by the ionic wind and by the transformation energy
The process of the appearance of charges on the plates of the capacitor +q and -q It can be imagined that portions of the charge are sequentially taken from one plate and transferred to another plate. The work of transferring the next portion is equal to:
where U is the voltage across the capacitor. Replacing U through the ratio of charge to capacity and passing to differentials, we get:
.
Integrating, we get:
![]() .
.
Electric field energy
The energy of a capacitor can be expressed in terms of quantities characterizing the electric field in the gap between the plates. Let's do this for a flat capacitor. Substitute in the expression for the energy of the capacitor expressions for the capacitance of a flat capacitor, then:
. (14.23)
Since , a S d=V- the volume occupied by the field, then you can write:
Formula (14.23) connects the energy of a capacitor with the charge on its plates, formula (14.24) - with the field strength. It is logical to raise the question: where is the energy localized (i.e. concentrated), what is the carrier of energy - charges or field? Within the limits of electrostatics, which studies the fields of fixed charges that are constant in time, it is impossible to give an answer to this question. Permanent fields and the charges that caused them cannot exist separately from each other. However, time-varying fields can exist independently of the charges that excite them and propagate in space in the form of electromagnetic waves. Experience shows that electromagnetic waves carry energy. Therefore, the energy carrier is the field.
If the field is homogeneous, the energy contained in it is distributed in space with a constant density equal to the field energy divided by the volume filled by the field. Therefore, the energy density of the flat capacitor field is:
This formula can be given the form:
replacing D(14.14), we obtain the energy density in the dielectric:
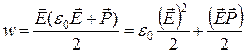 .
.
The first term coincides with the energy density of the field in vacuum. The second is the energy spent on the polarization of the dielectric.
CHAPTER 15. DIRECT ELECTRIC CURRENT
Strength and current density
electric shock any ordered (directed) movement of electric charges is called q. In a conductor under the action of an applied electric field E free electric charges move: positive - along the field, negative - against the field, i.e. an electric current is generated in a conductor called conduction current.
For the direction of the electric current conditionally take the direction of travel positive charges. The carriers of electricity in metal conductors are electrons, in semiconductors - electrons " holes, in liquid electrons ions, in gases ions and electrons.
The quantitative measure of electric current is current strength I - scalar physical quantity, defined electric charge passing through the cross section of the conductor per unit time:
A current whose strength and direction does not change with time is called permanent. For DC current strength I is a constant, so
Unit of current strength - ampere(AND). Physical quantity, determined by the amount of current passing through a unit area cross section conductor perpendicular to the direction of current is called current density:
But for direct current.
We express the strength and current density in terms of the speed of the ordered movement of charges in a metal conductor. If the concentration of current carriers is n and each carrier has elementary charge e, then in time through the cross section S conductor charge is transferred ![]() . Current strength
. Current strength
 ,
,
and current density
Current density - vector, oriented in the direction of current, i.e. the direction of the vector coincides with the direction of the ordered movement of positive charges. The unit of current density is (A / m 2).
Current through an arbitrary surface S is defined as the flow of the vector , i.e.
where dS = dS ( - unit vector of the normal to the site dS, constituting the angle a with the vector.
Third party forces. EMF.
If an electric field is created in the conductor and no measures are taken to maintain it, then the movement of charge carriers will very quickly lead to the disappearance of the field and the cessation of the current. To maintain the current, it is necessary to continuously remove the charges brought here by the current from the end of the conductor with a lower potential (the charge carriers are assumed to be positive), and continuously bring them to the end with a higher potential.
That is, it is necessary to carry out the circulation of charges, in which they would move along a closed path. The circulation of the electrostatic field voltage vector is zero
Therefore, in a closed circuit, along with areas where positive charges move in the direction of decreasing j, there must be areas where the transfer of positive charges occurs in the direction of increase j, i.e. against the forces of an electrostatic field (see Fig. 15.1). The movement of carriers in these areas is possible only with the help of forces of non-electrostatic origin, called outside forces. Thus, to maintain the current, external forces are needed that act either throughout the circuit or in its individual sections. They may be due chemical processes, diffusion of charge carriers in an inhomogeneous medium or through the boundary of two dissimilar substances, electric fields generated by time-varying magnetic fields.
The value equal to the work of external forces expended on moving a single positive charge is called the electromotive force (EMF) e acting in the chain or in its section
From a comparison of this formula with the formula that determines the potential: , it follows that the dimension of the EMF coincides with the dimension of the potential.
The external force acting on the charge can be represented as
The vector quantity is called field strength of external forces . The work of external forces on the charge throughout the closed circuit can be expressed as follows:
![]() .
.
Dividing this work by , we get the EMF acting in the circuit: e= . Thus, the EMF acting in a closed circuit can be defined as the circulation of the field strength vector of external forces.
The emf acting in section 1-2 is obviously equal to e 12 = .
In addition to external forces, the electrostatic field forces act on the charge
The resulting force acting at each point of the circuit on the charge is equal to
The work done by this force on the charge in the circuit section 1-2 is given by the expression
![]() e 12 .
e 12 .
The value numerically equal to the work done by electrostatic and external forces when moving a single positive charge is called voltage drop or simply voltage on this part of the circuit
e 12 .
In the absence of external forces, the voltage coincides with the potential difference.
Ohm's law
The German physicist G. Ohm (1787-1854) experimentally established in 1826 that the current strength I, flowing through a homogeneous metal conductor (i.e., a conductor in which external forces do not act), is proportional to the voltage U at the ends of the conductor:
where R- electrical resistance of the conductor. This equation expresses Ohm's law for a circuit section(not containing an emf source): the current strength in the conductor is directly proportional to the applied voltage and inversely proportional to the resistance of the conductor. This formula allows you to set the unit of resistance - ohm(Ohm): 1 Ohm is the resistance of such a conductor in which a direct current of 1 A flows at a voltage of 1 V.
The value is called electrical conductivity wire ika. Conductivity unit - Siemens(Cm): 1 Cm is the conductivity of a section of an electrical circuit with a resistance of 1 ohm. The resistance of conductors depends on its size and shape, as well as on the material from which the conductor is made. For a homogeneous linear conductor, the resistance R directly proportional to its length l and inversely proportional to its cross-sectional area S :
where r- coefficient of proportionality characterizing the material of the conductor. It is called electrical resistivity. The unit of electrical resistivity is Ohm×meter (Ohm×m).
Consider an inhomogeneous section of the circuit, where the effective EMF in section 1-2 will be denoted by e 12, and the potential difference applied at the ends of the section - through j 1 - j 2 .
If the current passes through motionless conductors forming section 1-2, then the work A 12 of all forces (external and electrostatic) performed on current carriers, according to the law of conservation and conversion of energy, is equal to the heat released in the section. The work of forces performed when moving a charge q 0 in section 1-2,
e 12 . (15.1)
EMF e 12 as well as current I is a scalar value. It must be taken either with a positive or with a negative sign, depending on the sign of the work done by external forces. If the EMF contributes to the movement of positive charges in the chosen direction (in the direction 1 -2 ), then e 12 > 0. If the EMF prevents the movement of positive charges in this direction, then e 12 <0.
During t heat is released in the conductor
From formulas (15.1) and (15.2) we obtain ![]() e 12 . (15.3)
e 12 . (15.3)
From here. (15.4)
Expression (15.3) or (15.4) is Ohm's law for an inhomogeneous section of a circuit in integral form, which is generalized Ohm's law.
 If in this section of the chain no current source(e 12 =0), then from (15.4) we arrive at Ohm's law for a homogeneous section of the chain: (in the absence of external forces, the voltage at the ends of the section is equal to the potential difference). If the electrical circuit closed then the chosen points 1 and 2 coincide, j 1 =j 2; then from (15.4) we get Ohm's law for a closed circuit: I \u003d e / R, where e- EMF acting in the circuit, R- the total resistance of the entire circuit. In general
If in this section of the chain no current source(e 12 =0), then from (15.4) we arrive at Ohm's law for a homogeneous section of the chain: (in the absence of external forces, the voltage at the ends of the section is equal to the potential difference). If the electrical circuit closed then the chosen points 1 and 2 coincide, j 1 =j 2; then from (15.4) we get Ohm's law for a closed circuit: I \u003d e / R, where e- EMF acting in the circuit, R- the total resistance of the entire circuit. In general
Rice. 15.2. R=r+R 1 , where r- internal resistance of the EMF source, R 1 - external circuit resistance. Therefore, Ohm's law for a closed circuit will have the form I = e /(r+r).