Limits and continuity
Sets
Under many is understood as a collection of homogeneous objects. Objects that form a set are called elements or dots of this multitude. Sets denote in capital letters, and their elements are lowercase. If a is an element of the set A, then the entry is used aÎ A. If b is not an element of the set A, then it is written like this: b Ï A. A set that does not contain a single element is called an empty set and is denoted as follows: Ø.
If the set B consists of part of the elements of the set A or coincides with it, then the set B called subset sets and denote BÌ A.
The two sets are called equal, if they consist of the same elements.
Association two sets A And B called a set C, consisting of all elements belonging to at least one of the sets: C=AÈ B.
By crossing two sets A And B called a set C, consisting of all elements belonging to each of these sets: C=AÇ B.
By difference sets A And B called a set E A, which do not belong to the set B: .
Supplement sets AÌ B called a set C, consisting of all elements of the set B, not belonging A.
Sets whose elements are real numbers are called numerical:
Wherein NÌ ZÌ QÌ R, IÌ R And R=IÈ Q.
A bunch of X, whose elements satisfy the inequality is called segment(segment) and is denoted by [ a; b]; inequality a<x<b – interval and is denoted by () ; inequalities and - half-intervals and are denoted by and respectively. You also often have to deal with infinite intervals and half-intervals: , , , and . It’s convenient to call them all at intervals .
Interval, i.e. set of points satisfying the inequality (where ), is called the -neighborhood of the point a.
The concept of function. Basic properties of a function
If each element x sets X a single element is matched y sets Y, then they say that on the set X given function y=f(x). Wherein x called independent variable or argument, A y – dependent variable or function, A f denotes the law of correspondence. A bunch of X called domain of definition functions, and a set Y – range of values functions.
There are several ways to specify functions.
1) Analytical method - the function is given by a formula of the form y=f(x).
2) Tabular method - the function is specified by a table containing the argument values and the corresponding function values y=f(x).
3) Graphical method - depicting a graph of a function, i.e. set of points ( x; y) coordinate plane, the abscissas of which represent the values of the argument, and the ordinates represent the corresponding values of the function y=f(x).
4) Verbal method - a function is described by the rule for its composition. For example, the Dirichlet function takes the value 1 if x is a rational number and 0 if x– irrational number.
The following main properties of functions are distinguished.
1 Even and odd Function y=f(x) is called even, if for any values x from its domain of definition is satisfied f(–x)=f(x), And odd, If f(–x)=–f(x). If none of the listed equalities is satisfied, then y=f(x) is called general function. The graph of an even function is symmetrical about the axis Oy, and the graph of the odd function is symmetrical about the origin.
2 Monotony Function y=f(x) is called increasing (decreasing) on the interval X, If higher value an argument from this interval corresponds to a larger (smaller) value of the function. Let x 1 ,x 2 Î X, x 2 >x 1 . Then the function increases on the interval X, If f(x 2)>f(x 1), and decreases if f(x 2)<f(x 1).
Along with increasing and decreasing functions, non-decreasing and non-increasing functions are considered. The function is called non-decreasing (non-increasing), if at x 1 ,x 2 Î X, x 2 >x 1 inequality holds f(x 2)≥f(x 1) (f(x 2)≤f(x 1)).
Increasing and decreasing functions, as well as non-increasing and non-decreasing functions are called monotonic.
3 Limited Function y=f(x) is called bounded on the interval X, if there is such a positive number M>0, what | f(x)|≤M for anyone xÎ X. Otherwise the function is said to be unbounded X.
4 Frequency Function y=f(x) is called periodic with a period T≠0, if for any x from the domain of the function f(x+T)=f(x). In what follows, by period we mean the smallest positive period of a function.
The function is called explicit, if it is given by a formula of the form y=f(x). If the function is given by the equation F(x, y)=0, not allowed relative to the dependent variable y, then it is called implicit.
Let y=f(x) is a function of the independent variable defined on the set X with range Y. Let's match each one yÎ Y single meaning xÎ X, at which f(x)=y.Then the resulting function x=φ (y), defined on the set Y with range X, called reverse and is designated y=f –1 (x). The graphs of mutually inverse functions are symmetrical with respect to the bisector of the first and third coordinate quarters.
Let the function y=f(u) is a function of a variable u, defined on the set U with range Y, and the variable u in turn is a function u=φ (x), defined on the set X with range U. Then given on the set X function y=f(φ (x)) is called complex function(composition of functions, superposition of functions, function of a function).
Elementary functions
The main elementary functions include:
From the basic elementary functions, new functions can be obtained using algebraic operations and superposition of functions.
Functions constructed from basic elementary functions using a finite number of algebraic operations and a finite number of superposition operations are called elementary.
Algebraic is a function in which a finite number of algebraic operations are performed on the argument. Algebraic functions include:
· an entire rational function (polynomial or polynomial)
· fractional-rational function (ratio of two polynomials)
· irrational function (if the operations on the argument include extracting the root).
Any non-algebraic function is called transcendental. Transcendental functions include exponential, logarithmic, trigonometric, and inverse trigonometric functions.
1) Function domain and function range.
The domain of a function is the set of all valid valid argument values x(variable x), for which the function y = f(x) determined. The range of a function is the set of all real values y, which the function accepts.
In elementary mathematics, functions are studied only on the set of real numbers.
2) Function zeros.
Function zero is argument value, at which the value of the function is equal to zero.
3) Intervals of constant sign of a function.
Intervals of constant sign of a function are sets of argument values on which the function values are only positive or only negative.
4) Monotonicity of the function.
An increasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a larger value of the function.
A decreasing function (in a certain interval) is a function in which a larger value of the argument from this interval corresponds to a smaller value of the function.
5) Even (odd) function.
An even function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality f(-x) = f(x). The graph of an even function is symmetrical about the ordinate.
An odd function is a function whose domain of definition is symmetrical with respect to the origin and for any X from the domain of definition the equality is true f(-x) = - f(x). The graph of an odd function is symmetrical about the origin.
6) Limited and unlimited functions.
A function is called bounded if there is a positive number M such that |f(x)| ≤ M for all values of x. If such a number does not exist, then the function is unlimited.
7) Periodicity of the function.
A function f(x) is periodic if there is a non-zero number T such that for any x from the domain of definition of the function the following holds: f(x+T) = f(x). This smallest number is called the period of the function. All trigonometric functions are periodic. (Trigonometric formulas).
19. Basic elementary functions, their properties and graphs. Application of functions in economics.
Linear function is called a function of the form , where x is a variable, a and b are real numbers.
Number A called slope straight line, it is equal to the tangent of the angle of inclination of this straight line to the positive direction of the abscissa axis. The graph of a linear function is a straight line. It is defined by two points.
1. Domain of definition - the set of all real numbers: D(y)=R
2. The set of values is the set of all real numbers: E(y)=R
3. The function takes a zero value when or.
4. The function increases (decreases) over the entire domain of definition.
5. A linear function is continuous over the entire domain of definition, differentiable and .
A function of the form, where x is a variable, coefficients a, b, c are real numbers, is called quadratic
The domain of definition and the range of values of a function. In elementary mathematics, functions are studied only on the set of real numbers R.This means that the function argument can only take those real values for which the function is defined, i.e. it also accepts only real values. A bunch of X all valid valid argument values x, for which the function y= f(x)defined, called domain of the function. A bunch of Y all real values y, which the function accepts, is called function range. Now we can give a more precise definition of the function: rule(law) of correspondence between sets X and Y, according to which for each element from the setX can find one and only one element from the set Y, called a function.
From this definition it follows that a function is considered defined if:
The domain of the function is specified X ;
The function range is specified Y ;
The rule (law) of correspondence is known, and such that for each
Only one function value can be found for an argument value.
This requirement of uniqueness of the function is mandatory.
Monotonic function. If for any two values of the argument x 1 and x 2 of the condition x 2 > x 1 follows f(x 2) > f(x 1), then the function f(x) is called increasing; if for any x 1 and x 2 of the condition x 2 > x 1 follows f(x 2) < f(x 1), then the function f(x) is called decreasing. A function that only increases or only decreases is called monotonous.
Limited and unlimited functions. The function is called limited, if there is such a positive number M what | f(x) | M for all values x. If such a number does not exist, then the function is unlimited.
EXAMPLES.
The function shown in Fig. 3 is limited, but not monotonic. The function in Fig. 4 is just the opposite, monotonic, but unlimited. (Explain this please!).
Continuous and discontinuous functions. Function y = f (x) is called continuous at the pointx = a, If:
1) the function is defined when x = a, i.e. f (a) exists;
2) exists finite limit lim f (x) ;
x→a
(see Function Limits)
3) f (a) = lim f (x) .
x→a
If at least one of these conditions is not met, then the function is called explosive at the point x = a.
If the function is continuous during everyone points of its domain of definition, then it is called continuous function.
Even and odd functions. If for any x f(- x) = f (x), then the function is called even;if it occurs: f(- x) = - f (x), then the function is called odd. Graph of an even function symmetrical about the Y axis(Fig. 5), a graph odd function Simmetric with respect to the origin(Fig. 6).
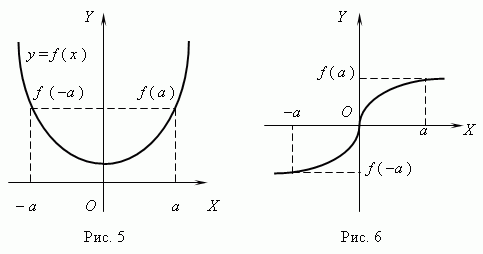
Periodic function. Function f (x) - periodic, if such a thing exists non-zero number T what for any x from the domain of definition of the function the following holds: f (x + T) = f (x). This least the number is called period of the function. All trigonometric functions are periodic.
Example 1. Prove that sin x has a period of 2.
Solution: We know that sin ( x+ 2n) = sin x, Where n= 0, ± 1, ± 2, …
Therefore, addition 2 n not to the sine argument
Changes its meaning. Is there another number with this
Same property?
Let's pretend that P- such a number, i.e. equality:
Sin ( x+ P) = sin x,
Valid for any value x. But then it has
Place and time x= / 2, i.e.
Sin(/2 + P) = sin / 2 = 1.
But according to the reduction formula sin ( / 2 + P) = cos P. Then
From the last two equalities it follows that cos P= 1, but we
We know that this is true only when P = 2n. Since the smallest
A non-zero number from 2 n is 2, then this number
And there is a period sin x. It can be proven in a similar way that 2 from n is , so this is the period sin 2 x.
Function zeros. The argument value at which the function is equal to 0 is called zero (root) function. A function can have multiple zeros. For example, the function y = x (x + 1) (x-3) has three zeros: x= 0, x= -1, x= 3. Geometrically null function - this is the abscissa of the point of intersection of the function graph with the axis X .
Figure 7 shows a graph of a function with zeros: x= a, x = b And x= c.
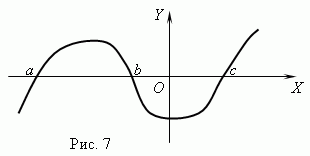
Asymptote. If the graph of a function indefinitely approaches a certain line as it moves away from the origin, then this line is called asymptote.
The properties and graphs of power functions are presented for different meanings exponent. Basic formulas, domains of definition and sets of values, parity, monotonicity, increasing and decreasing, extrema, convexity, inflections, points of intersection with coordinate axes, limits, particular values.
On the domain of definition power function y = x p the following formulas apply:
;
;
;
;
;
;
;
;
.
If the exponent of the power function y = x p is equal to zero, p = 0, then the power function is defined for all x ≠ 0 and is a constant equal to one:
y = x p = x 0 = 1, x ≠ 0.
Consider a power function y = x p = x n with a natural odd exponent n = 1, 3, 5, ... . This indicator can also be written in the form: n = 2k + 1, where k = 0, 1, 2, 3, ... is a non-negative integer. Below are the properties and graphs of such functions.
Graph of a power function y = x n with a natural odd exponent for various values of the exponent n = 1, 3, 5, ....
Domain: -∞ < x < ∞
Multiple meanings: -∞ < y < ∞
Parity: odd, y(-x) = - y(x)
Monotone: monotonically increases
Extremes: No
Convex:
at -∞< x < 0
выпукла вверх
at 0< x < ∞
выпукла вниз
Inflection points: x = 0, y = 0
x = 0, y = 0
Limits:
;
Private values:
at x = -1,
y(-1) = (-1) n ≡ (-1) 2k+1 = -1
at x = 0, y(0) = 0 n = 0
for x = 1, y(1) = 1 n = 1
Reverse function:
for n = 1, the function is its inverse: x = y
for n ≠ 1, the inverse function is the root of degree n:
Consider a power function y = x p = x n with a natural even exponent n = 2, 4, 6, ... . This indicator can also be written in the form: n = 2k, where k = 1, 2, 3, ... - natural. The properties and graphs of such functions are given below.
Graph of a power function y = x n with a natural even exponent for various values of the exponent n = 2, 4, 6, ....
Domain: -∞ < x < ∞
Multiple meanings: 0 ≤ y< ∞
Parity: even, y(-x) = y(x)
Monotone:
for x ≤ 0 monotonically decreases
for x ≥ 0 monotonically increases
Extremes: minimum, x = 0, y = 0
Convex: convex down
Inflection points: No
Intersection points with coordinate axes: x = 0, y = 0
Limits:
;
Private values:
at x = -1, y(-1) = (-1) n ≡ (-1) 2k = 1
at x = 0, y(0) = 0 n = 0
for x = 1, y(1) = 1 n = 1
Reverse function:
for n = 2, Square root:
for n ≠ 2, root of degree n:
Consider a power function y = x p = x n with an integer negative exponent n = -1, -2, -3, ... . If we put n = -k, where k = 1, 2, 3, ... is a natural number, then it can be represented as:
Graph of a power function y = x n with a negative integer exponent for various values of the exponent n = -1, -2, -3, ... .
Below are the properties of the function y = x n with an odd negative exponent n = -1, -3, -5, ....
Domain: x ≠ 0
Multiple meanings: y ≠ 0
Parity: odd, y(-x) = - y(x)
Monotone: monotonically decreases
Extremes: No
Convex:
at x< 0
:
выпукла вверх
for x > 0: convex downward
Inflection points: No
Intersection points with coordinate axes: No
Sign:
at x< 0, y < 0
for x > 0, y > 0
Limits:
; ; ;
Private values:
for x = 1, y(1) = 1 n = 1
Reverse function:
when n = -1,
at n< -2
,
Below are the properties of the function y = x n with an even negative exponent n = -2, -4, -6, ....
Domain: x ≠ 0
Multiple meanings: y > 0
Parity: even, y(-x) = y(x)
Monotone:
at x< 0
:
монотонно возрастает
for x > 0: monotonically decreases
Extremes: No
Convex: convex down
Inflection points: No
Intersection points with coordinate axes: No
Sign: y > 0
Limits:
; ; ;
Private values:
for x = 1, y(1) = 1 n = 1
Reverse function:
at n = -2,
at n< -2
,
Consider a power function y = x p with a rational (fractional) exponent, where n is an integer, m > 1 is a natural number. Moreover, n, m do not have common divisors.
Let the denominator of the fractional exponent be odd: m = 3, 5, 7, ... . In this case, the power function x p is defined for both positive and negative values of the argument x. Let us consider the properties of such power functions when the exponent p is within certain limits.
Let the rational exponent (with odd denominator m = 3, 5, 7, ...) less than zero: .
Graphs of power functions with a rational negative exponent for various values of the exponent, where m = 3, 5, 7, ... - odd.
We present the properties of the power function y = x p with a rational negative exponent, where n = -1, -3, -5, ... is an odd negative integer, m = 3, 5, 7 ... is an odd natural integer.
Domain: x ≠ 0
Multiple meanings: y ≠ 0
Parity: odd, y(-x) = - y(x)
Monotone: monotonically decreases
Extremes: No
Convex:
at x< 0
:
выпукла вверх
for x > 0: convex downward
Inflection points: No
Intersection points with coordinate axes: No
Sign:
at x< 0, y < 0
for x > 0, y > 0
Limits:
; ; ;
Private values:
at x = -1, y(-1) = (-1) n = -1
for x = 1, y(1) = 1 n = 1
Reverse function:
Properties of the power function y = x p with a rational negative exponent, where n = -2, -4, -6, ... is an even negative integer, m = 3, 5, 7 ... is an odd natural integer.
Domain: x ≠ 0
Multiple meanings: y > 0
Parity: even, y(-x) = y(x)
Monotone:
at x< 0
:
монотонно возрастает
for x > 0: monotonically decreases
Extremes: No
Convex: convex down
Inflection points: No
Intersection points with coordinate axes: No
Sign: y > 0
Limits:
; ; ;
Private values:
at x = -1, y(-1) = (-1) n = 1
for x = 1, y(1) = 1 n = 1
Reverse function:
Graph of a power function with rational exponent (0< p < 1 ) при различных значениях показателя степени , где m = 3, 5, 7, ... - нечетное.
< p < 1 , где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
Domain: -∞ < x < +∞
Multiple meanings: -∞ < y < +∞
Parity: odd, y(-x) = - y(x)
Monotone: monotonically increases
Extremes: No
Convex:
at x< 0
:
выпукла вниз
for x > 0: convex upward
Inflection points: x = 0, y = 0
Intersection points with coordinate axes: x = 0, y = 0
Sign:
at x< 0, y < 0
for x > 0, y > 0
Limits:
;
Private values:
at x = -1, y(-1) = -1
at x = 0, y(0) = 0
for x = 1, y(1) = 1
Reverse function:
The properties of the power function y = x p with a rational exponent within 0 are presented< p < 1 , где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.
Domain: -∞ < x < +∞
Multiple meanings: 0 ≤ y< +∞
Parity: even, y(-x) = y(x)
Monotone:
at x< 0
:
монотонно убывает
for x > 0: increases monotonically
Extremes: minimum at x = 0, y = 0
Convex: convex upward for x ≠ 0
Inflection points: No
Intersection points with coordinate axes: x = 0, y = 0
Sign: for x ≠ 0, y > 0
Limits:
;
Private values:
at x = -1, y(-1) = 1
at x = 0, y(0) = 0
for x = 1, y(1) = 1
Reverse function:
Graph of a power function with a rational exponent (p > 1) for various values of the exponent, where m = 3, 5, 7, ... - odd.
Properties of the power function y = x p with a rational exponent greater than one: . Where n = 5, 7, 9, ... - odd natural, m = 3, 5, 7 ... - odd natural.
Domain: -∞ < x < ∞
Multiple meanings: -∞ < y < ∞
Parity: odd, y(-x) = - y(x)
Monotone: monotonically increases
Extremes: No
Convex:
at -∞< x < 0
выпукла вверх
at 0< x < ∞
выпукла вниз
Inflection points: x = 0, y = 0
Intersection points with coordinate axes: x = 0, y = 0
Limits:
;
Private values:
at x = -1, y(-1) = -1
at x = 0, y(0) = 0
for x = 1, y(1) = 1
Reverse function:
Properties of the power function y = x p with a rational exponent greater than one: . Where n = 4, 6, 8, ... - even natural, m = 3, 5, 7 ... - odd natural.
Domain: -∞ < x < ∞
Multiple meanings: 0 ≤ y< ∞
Parity: even, y(-x) = y(x)
Monotone:
at x< 0
монотонно убывает
for x > 0 monotonically increases
Extremes: minimum at x = 0, y = 0
Convex: convex down
Inflection points: No
Intersection points with coordinate axes: x = 0, y = 0
Limits:
;
Private values:
at x = -1, y(-1) = 1
at x = 0, y(0) = 0
for x = 1, y(1) = 1
Reverse function:
Let the denominator of the fractional exponent be even: m = 2, 4, 6, ... . In this case, the power function x p is not defined for negative values of the argument. Its properties coincide with the properties of a power function with an irrational exponent (see the next section).
Consider a power function y = x p with an irrational exponent p. The properties of such functions differ from those discussed above in that they are not defined for negative values of the argument x. For positive values of the argument, the properties depend only on the value of the exponent p and do not depend on whether p is integer, rational, or irrational.
y = x p for different values of the exponent p.
Domain: x > 0
Multiple meanings: y > 0
Monotone: monotonically decreases
Convex: convex down
Inflection points: No
Intersection points with coordinate axes: No
Limits: ;
Private meaning: For x = 1, y(1) = 1 p = 1
Domain: x ≥ 0
Multiple meanings: y ≥ 0
Monotone: monotonically increases
Convex: convex upward
Inflection points: No
Intersection points with coordinate axes: x = 0, y = 0
Limits:
Private values: For x = 0, y(0) = 0 p = 0 .
For x = 1, y(1) = 1 p = 1
Domain: x ≥ 0
Multiple meanings: y ≥ 0
Monotone: monotonically increases
Convex: convex down
Inflection points: No
Intersection points with coordinate axes: x = 0, y = 0
Limits:
Private values: For x = 0, y(0) = 0 p = 0 .
For x = 1, y(1) = 1 p = 1
References:
I.N. Bronstein, K.A. Semendyaev, Handbook of mathematics for engineers and college students, “Lan”, 2009.
Russian gymnasium
ABSTRACT
Completed
student of class 10 “F” Burmistrov Sergey
Supervisor
mathematic teacher
Yulina O.A.
Nizhny Novgorod
Function and its properties
Function- variable dependence at from variable x , if each value X matches a single value at .
Variable x- independent variable or argument.
Variable y- dependent variable
Function value- meaning at, corresponding to the specified value X .
The scope of the function is all the values that the independent variable takes.
Function range (set of values) - all the values that the function accepts.
The function is even- if for anyone X f(x)=f(-x)
The function is odd- if for anyone X from the domain of definition of the function the equality f(-x)=-f(x)
Increasing function- if for any x 1 And x 2, such that x 1
<
x 2, the inequality holds f(
x 1
)
Decreasing function- if for any x 1 And x 2, such that x 1 < x 2, the inequality holds f( x 1 )>f( x 2 )
Methods for specifying a function
¨ To define a function, you need to specify a way in which, for each argument value, the corresponding function value can be found. The most common way to specify a function is using a formula at =f(x), Where f(x)- expression with a variable X. In this case, they say that the function is given by a formula or that the function is given analytically.
¨ In practice it is often used tabular way to specify a function. With this method, a table is provided indicating the function values for the argument values available in the table. Examples of table functions are a table of squares and a table of cubes.
Types of functions and their properties
1) Constant function - function given by formula y= b , Where b- some number. The graph of the constant function y=b is a straight line parallel to the abscissa axis and passing through the point (0;b) on the ordinate axis
2) Direct proportionality - function given by formula y= kx , where k¹0. Number k called proportionality factor .
Function properties y=kx :
1. The domain of a function is the set of all real numbers
2. y=kx- odd function
3. When k>0 the function increases, and when k<0 убывает на всей числовой прямой
3)Linear function- function, which is given by the formula y=kx+b, Where k And b - real numbers. If in particular k=0, then we get a constant function y=b; If b=0, then we get direct proportionality y=kx .
Function Properties y=kx+b :
1. Domain - the set of all real numbers
2. Function y=kx+b general form, i.e. neither even nor odd.
3. When k>0 the function increases, and when k<0 убывает на всей числовой прямой
The graph of the function is straight .
4)Inverse proportionality- function given by formula y=k /X, where k¹0 Number k called coefficient of inverse proportionality.
Function Properties y=k / x:
1. Domain - the set of all real numbers except zero
2. y=k / x - odd function
3. If k>0, then the function decreases on the interval (0;+¥) and on the interval (-¥;0). If k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).
The graph of the function is hyperbola .
5)Function y=x2
Function Properties y=x2:
2. y=x2 - even function
3. On the interval the function decreases
The graph of the function is parabola .
6)Function y=x 3
Function Properties y=x 3:
1. Domain of definition - the entire number line
2. y=x 3 - odd function
3. The function increases along the entire number line
The graph of the function is cubic parabola
7)Power function with natural exponent - function given by formula y=xn, Where n- natural number. When n=1 we obtain the function y=x, its properties are discussed in paragraph 2. For n=2;3 we obtain the functions y=x 2 ; y=x 3 . Their properties are discussed above.
Let n be an arbitrary even number greater than two: 4,6,8... In this case, the function y=xn has the same properties as the function y=x 2. The graph of the function resembles a parabola y=x 2, only the branches of the graph for |x|>1 rise steeper the larger n, and for |x|<1 тем “теснее прижимаются” к оси Х, чем больше n.
Let n be an arbitrary odd number greater than three: 5,7,9... In this case, the function y=xn has the same properties as the function y=x 3 . The graph of the function resembles a cubic parabola.
8)Power function with a negative integer exponent - function given by formula y=x -n , Where n- natural number. For n=1 we obtain y=1/x; the properties of this function are discussed in paragraph 4.
Let n be an odd number greater than one: 3,5,7... In this case, the function y=x -n has basically the same properties as the function y=1/x.
Let n be an even number, for example n=2.
Function Properties y=x -2 :
1. The function is defined for all x¹0
2. y=x -2 - even function
3. The function decreases by (0;+¥) and increases by (-¥;0).
Any functions with even n greater than two have the same properties.
9)Function y= Ö X
Function Properties y= Ö X :
1. Domain of definition - ray)
