
Everyone knows that electric charges do not interact directly with each other. Every charged body, including the space around it, is surrounded by an active electric field. Therefore, the interaction occurs not directly between the charges themselves, but between the electric fields surrounding them. Everyone has a certain force, the magnitude of which has a direct effect on any charge. The ability to interact is considered one of the main characteristics of the field.
To explore electric field, located around an object with an electric charge, a so-called test charge is used. Usually, a point charge with an insignificant value is used, which is called a test charge and does not have a noticeable effect on the main charge under study.
In order to maximum accuracy determine the quantitative parameters of charged objects, there are special quantities that represent tension lines electric field. This is due to the fact that tension itself is a stable physical quantity. The intensity value is calculated as the ratio of the field strength with which it acts on the test charge to the magnitude of this charge. IN in this case the test charge has a positive value and is located at a certain point.
Lines of tension are its main characterizing indicator. They represent a vector physical quantity. Their direction at any point in space coincides with the direction of the force acting on the test positive charge. Charges that are stationary and do not change over time have an electrostatic electric field.
When studying electric fields created by several charged bodies at once, the value of their total strength will be the sum of the geometric values of each individual charged body influencing the test charge. Therefore, electric field lines include the sum of all electric field lines that are created by charges at each individual point.
Thus, field lines clearly display graphical indicators of electric fields. At each individual point, they have a direction towards the tangent, which is located in strict relation to them. The number of tension lines is proportional to the general vector of the electric field strength.
To depict the electric field in the space surrounding the charge, you can use intensity vectors (Fig. 15.3): This method of depiction is time consuming and not always convenient. Faraday proposed to represent the field by lines of force, which we will henceforth call lines of tension. One of these lines is drawn through point A so that vector E is directed along it. By drawing a series of straight lines from the charge in this way, we obtain an image of the field by lines of intensity (Fig. 15.4).
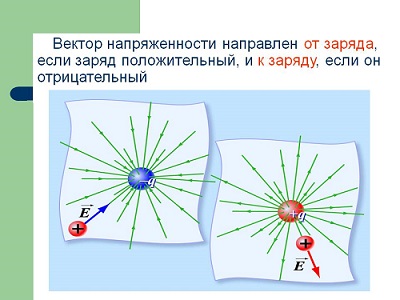
To distinguish between images of fields of positive and negative charges, the intensity line is considered to be directed in the direction where the intensity vector E points.
Then the fields of positive and negative charges will differ in the direction of the tension lines (Fig. 15.4).

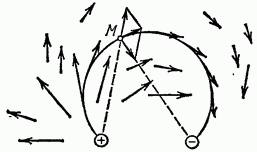
It is more difficult to draw tension lines when the field is created by several charges, for example two. In most cases, it is impossible to draw a line so that the tension vectors depicted at each point lie entirely on it. But you can always draw a curved line so that the tension vectors are tangent to it everywhere. One such line is drawn through point M in Fig. 15.5, which shows the field strength vectors of two equal opposite charges. (Think about why only one line can be drawn through each point of the field using the indicated method.)
So, a tension line is such a line, at each point of which the field strength vector is directed tangentially. In Fig. 15.6 and 15.7, the intensity lines depict the fields of equal-sized opposite and like charges.
When depicting the field graphically, it should be remembered that the electric field strength lines:
1) do not intersect with each other anywhere;
2) have a beginning on a positive charge (or at infinity
and end on the negative (or at infinity), that is, they are open lines;
3) between charges they are not interrupted anywhere.
The picture of the field depicted by tension lines will be clearer if we agree to draw these lines more densely where the field strength is greater. So, the density of tension lines must be proportional to E.
When calculating, it is conventionally assumed that through a unit of surface area located perpendicular to the lines of tension, a number of lines pass through, which is numerically equal to E at that location. where is this surface located? (Think about where the tension is greater in Figures 15.6 and 15.7 and how the tension vector is directed at three randomly selected points in the field in each figure.)
Coulomb's law, studied in the last lesson, was established experimentally and is valid for charged bodies at rest. How does the interaction of charged bodies at a distance occur? Until some time when studying electrical interactions Two fundamentally different theories developed side by side: short range theory And long-range theory(actions at a distance).
The theory of short-range action is that charged bodies interact with each other through an intermediate link (for example, the chain in the problem of lifting a bucket from a well is an intermediate link through which we act on the bucket, that is, we lift it).
The theory of long-range interaction states that charged bodies interact through emptiness. Charles Coulomb adhered to precisely this theory and said that charged bodies “feel” each other. IN early XIX century, Michael Faraday put an end to the debate (Fig. 1). In works related to the electric field, he established that between charged bodies there is a certain object, which carries out the action of charged bodies on each other. Michael Faraday's work was confirmed by James Maxwell (Fig. 2). He showed that the action of one charged body on another extends in a finite time, thus, between the charged bodies there must be an intermediate link through which the interaction occurs.

Rice. 2. James Clerk Maxwell ()
Definition: Electric field- This special shape matter, which is created by charges at rest and is determined by the action on other charges.
The electric field is characterized by certain values. One of them is called tension.
Recall that according to Coulomb's law, the force of interaction between two charges is:
where l is the distance between charged particles, and c is the speed of light, the speed of propagation of electromagnetic waves.
Let's consider an experiment on the interaction of two charges. Let the electric field be created by a positive charge +q 0, and a test, point positive charge +q is placed in this field at a certain distance (Fig. 3a). According to Coulomb's law, the test charge will be subject to the force of electrostatic interaction from the charge creating the electric field. Then the ratio of this force to the value of the test charge will characterize the action of the electric field at a given point. If twice the test charge is placed at this point, then the interaction force will also double (Fig. 3, b). Similarly, the ratio of the force to the magnitude of the test charge will again give the value of the action of the electric field at a given point. The effect of the electric field is also determined if the test charge is negative (Fig. 3, c).
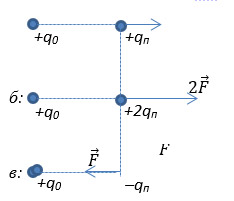
Rice. 3. The force of electrostatic interaction between two point charges
Thus, at the point where the test charge is located, the field is characterized by the value:
Tension is a vector quantity and is power characteristic of the electric field, is directed in the same direction as the force of electrostatic interaction. It shows how strong the electric field acts on a charge placed in it.
Let us consider the electric field strength of a solitary point charge or a charged sphere.
From the definition of the intensity it follows that for the case of interaction of two point charges, knowing the strength of their Coulomb interaction, we can obtain the magnitude of the electric field strength that is created by the charge q 0 at a point at a distance r from it to the point at which the electric field is being studied:
This formula shows that the field strength of a point charge changes in inverse proportion to the square of the distance from a given charge, that is, for example, when the distance doubles, the strength decreases fourfold.
Let us now try to characterize the electrostatic field of several charges. In this case, it is necessary to use the addition of the vector values of the intensities of all charges. Let's introduce a test charge and write down the sum of the vectors of forces acting on this charge. The resulting tension value is obtained by dividing the values of these forces by the value of the test charge. This method is called superposition principle.
Tension electrostatic field It is customary to depict graphically using power lines, which are also called tension lines. Such an image can be obtained by constructing field strength vectors at as many points as possible near a given charge or an entire system of charged bodies.
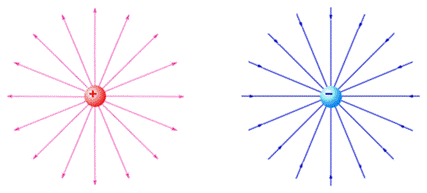
a) positive b) negative
Rice. 4. Lines of electric field strength of a point charge ()
Let's look at several examples of images of field lines. The tension lines come out of the positive charge (Fig. 4, a), that is, the positive charge is the source of the force lines. The tension lines end at the negative charge (Fig. 4,b).
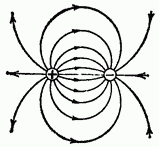
Let us now consider a system consisting of positive and negative charges located at a finite distance from each other (Fig. 5). In this case, the tension lines are directed from the positive charge to the negative one.
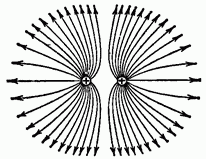
Of great interest is the electric field between two infinite planes. If one of the plates is charged positively and the other negatively, then in the gap between the planes a homogeneous an electrostatic field, the lines of intensity of which turn out to be parallel to each other (Fig. 6).
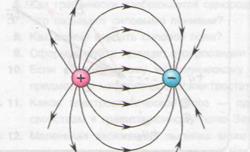
Rice. 5. Tension lines of a system of two charges ()
![]()
Rice. 6. Field strength lines between charged plates ()
When heterogeneous Electric field strength is determined by the density of the field lines: where the field lines are denser, the field strength is greater (Fig. 7).
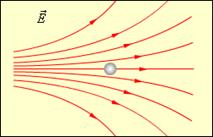
Rice. 7. Non-uniform electric field ()
Definition: Tension lines are continuous lines whose tangents at each point coincide with the tension vectors at that point.
Tension lines begin at positive charges, end at negative charges, and are continuous.
We can depict the electric field using lines of force as we see fit, that is, the number of lines of force and their density are not limited in any way. But in this case it is necessary to take into account the direction of the field strength vectors and their absolute values.
The following remark is very important. As mentioned earlier, Coulomb's law is applicable only for point charges at rest, as well as charged balls and spheres. Tension makes it possible to characterize the electric field regardless of the shape of the charged body that this field creates.
Bibliography
Homework