Transfer równoległy.
TŁUMACZENIE WZDŁUŻ OSI Y
f(x) => f(x) - b
Załóżmy, że chcesz zbudować wykres funkcji y = f(x) - b. Łatwo zauważyć, że rzędne tego wykresu dla wszystkich wartości x na |b| jednostki mniejsze niż odpowiadające im rzędne wykresu funkcji y = f(x) dla b>0 i |b| jednostki więcej - w b 0 lub w górę w b Aby wykreślić wykres funkcji y + b = f(x), należy skonstruować wykres funkcji y = f(x) i przesunąć oś x do |b| jednostki w górę przy b>0 lub o |b| jednostki w dół w b
TRANSFER WZDŁUŻ OSI ABSCIS
f(x) => f(x + a)
Załóżmy, że chcesz wykreślić funkcję y = f(x + a). Rozważmy funkcję y = f(x), która w pewnym momencie x = x1 przyjmuje wartość y1 = f(x1). Oczywiście funkcja y = f(x + a) przyjmie tę samą wartość w punkcie x2, którego współrzędna wyznaczana jest z równości x2 + a = x1, tj. x2 = x1 - a, a rozważana równość obowiązuje dla ogółu wszystkich wartości z dziedziny definicji funkcji. Zatem wykres funkcji y = f(x + a) można otrzymać przesuwając równolegle wykres funkcji y = f(x) wzdłuż osi x w lewo o |a| jednostki dla a > 0 lub w prawo o |a| jednostki dla a Aby skonstruować wykres funkcji y = f(x + a), należy skonstruować wykres funkcji y = f(x) i przesunąć oś rzędnych do |a| jednostki w prawo, gdy a>0 lub przez |a| jednostki po lewej stronie w a
Przykłady:
1.y=f(x+a)
2.y=f(x)+b
Odbicie.
BUDOWA WYKRESU FUNKCJI FORMY Y = F(-X)
f(x) => f(-x)
Jest oczywiste, że funkcje y = f(-x) i y = f(x) przyjmują równe wartości w punktach, których odcięte są równe w wartości bezwzględnej, ale przeciwne pod względem znaku. Innymi słowy, współrzędne wykresu funkcji y = f(-x) w obszarze dodatnich (ujemnych) wartości x będą równe rzędnym wykresu funkcji y = f(x) dla odpowiednich ujemnych (dodatnich) wartości x w wartości bezwzględnej. W ten sposób otrzymujemy następującą regułę.
Aby wykreślić funkcję y = f(-x), należy wykreślić funkcję y = f(x) i odzwierciedlić ją względem rzędnej. Powstały wykres jest wykresem funkcji y = f(-x)
KONSTRUKCJA WYKRESU FUNKCJI FORMY Y = - F(X)
f(x) => - f(x)
Współrzędne wykresu funkcji y = - f(x) dla wszystkich wartości argumentu są równe co do wartości bezwzględnej, ale przeciwne pod względem znaku do rzędnych wykresu funkcji y = f(x) dla te same wartości argumentu. W ten sposób otrzymujemy następującą regułę.
Aby wykreślić wykres funkcji y = - f(x), należy wykreślić wykres funkcji y = f(x) i odzwierciedlić go względem osi x.
Przykłady:
1.y=-f(x)
2.y=f(-x)
3.y=-f(-x)
Odkształcenie.
DEFORMACJA WYKRESU WZDŁUŻ OSI Y
f(x) => k f(x)
Rozważmy funkcję o postaci y = k f(x), gdzie k > 0. Łatwo zauważyć, że przy równych wartościach argumentu rzędne wykresu tej funkcji będą k razy większe od rzędnych wykres funkcji y = f(x) dla k > 1 lub 1/k razy mniej niż rzędne wykresu funkcji y = f(x) dla k Aby skonstruować wykres funkcji y = k f(x ), należy skonstruować wykres funkcji y = f(x) i zwiększyć jej rzędne k razy dla k > 1 (rozciągnąć wykres wzdłuż osi rzędnych ) lub zmniejszyć jej rzędne 1/k razy w k
k > 1- rozciąganie od osi Wołu
0 - kompresja do osi OX
DEFORMACJA WYKRESU WZDŁUŻ OSI ABSCIS
f(x) => f(kx)
Niech będzie konieczne skonstruowanie wykresu funkcji y = f(kx), gdzie k>0. Rozważmy funkcję y = f(x), która w dowolnym punkcie x = x1 przyjmuje wartość y1 = f(x1). Jest oczywiste, że funkcja y = f(kx) przyjmuje tę samą wartość w punkcie x = x2, którego współrzędna jest określona przez równość x1 = kx2, a równość ta obowiązuje dla ogółu wszystkich wartości x z dziedziny definicji funkcji. W rezultacie wykres funkcji y = f(kx) okazuje się skompresowany (dla k 1) wzdłuż osi odciętych względem wykresu funkcji y = f(x). W ten sposób otrzymujemy regułę.
Aby skonstruować wykres funkcji y = f(kx), należy skonstruować wykres funkcji y = f(x) i zmniejszyć jej odcięte k razy dla k>1 (ścisnąć wykres wzdłuż osi odciętych) lub zwiększyć jego odcięte o 1/k razy dla k
k > 1- kompresja do osi Oy
0 - rozciąganie od osi OY
§ 11. Wykresy sinusa i cosinusa | ||||||
Powtórz: § 5. Zegar, lub nowoczesny wygląd do trygonometrii. |
||||||
Narysujmy funkcję y = sin x. Jednocześnie znowu musimy |
||||||
odpowiedni jest zegar z § 5. | ||||||
Jeśli x = 0, to oczywiście y = 0. Gdy x wynosi | ||||||
topi się od 0 do π/2, liczba sin x wzrasta od 0 do | ||||||
1 (wyobraź sobie, jak rzędna połączenia | ||||||
tsa w ręce naszych markowych zegarków). Działka | ||||||
Wykres dla x od 0 do π/2 pokazano na ryc. 11.1. | ||||||
Dla małego x nasz wykres jest zbliżony do linii prostej | ||||||
y = x: pamiętaj, że dla małego x obowiązuje następująca reguła: | ||||||
przybliżony wzór sin x ≈ x. Można powiedzieć | ||||||
że prosta y = x jest styczna do krzywej z równaniem | ||||||
y = grzech x w punkcie (0; 0). Należy również pamiętać, że nasza część wykresu |
||||||
znajduje się poniżej tej linii: przecież dla ostre zakręty x, zmierzone |
||||||
w radianach, nierówność sin x< x. | ||||||
Im bliżej x jest π/2, tym bardziej płaska jest nasza krzywa. Ten |
||||||
następuje wskutek rzutu końca strzałki na oś rzędnych, |
||||||
oscylujące wzdłuż odcinka [−1; 1], najszybciej porusza się w środku |
||||||
segmentu i zwalnia na jego krawędziach: mówiliśmy już o tym w § 5. |
||||||
od π do 3π/2, sin x maleje od 0 do −1, a gdy x wzrasta od 3π/2 do 2π, wzrasta od −1 do 0. Zatem fragment wykresu dla 0 6 x 6 2π jest gotowy (Rys. 11.2 b ). Przy okazji zauważmy, że krzywa na rys. 11.2 a jest symetryczna względem prostej pionowej o równaniu x = π/2. W rzeczywistości wzór redukcyjny sin(π/2 − x) = sin x pokazuje, że punkty z odciętymi x i π − x mają na wykresie te same rzędne, a zatem są symetryczne względem prostej x = π/ 2 (ryc. 11.3 A).
Zadanie 11.1. Zapisz równanie prostej stycznej do wykresu funkcji y = sin x w punkcie o współrzędnych (π; 0).
Krzywa na rys. 11.2 b jest centralnie symetryczna względem punktu o współrzędnych (π; 0); wynika to z innego wzoru redukcyjnego: sin(2π − x) = − sin x (Rys. 11.3 b).
Kiedy już mamy fragment wykresu funkcji y = sin x dla 0 6 x 6 2π, cały wykres jest łatwy do skonstruowania. W rzeczywistości, gdy koniec strzały przebył odległość 2π, strzałka powróciła do swojego pierwotnego położenia; przy dalszym ruchu wszystko się powtórzy. Oznacza to, że wykres będzie składał się z tych samych fragmentów, co na ryc. 11.2 b. Ostateczny wykres funkcji y = sin x wygląda jak na rys. 11.4. W tym przypadku odcinki wykresu w x , , [−2π; 0],. . . uzyskuje się z wykresu na ryc. 11.2 b poprzez przesunięcie wzdłuż osi odciętych o 2π, 4π, −2π,. . . odpowiednio. Jest to po prostu powtórzenie faktu, że funkcja y = sin x ma okres 2π.
Ryż. 11.4. y = grzech x.
Ryż. 11,5. y = cos x.
Teraz narysujmy funkcję y = cos x. Można by go zbudować w taki sam sposób, w jaki zbudowaliśmy wykres sinusoidalny. My jednak wybierzemy inną ścieżkę, która pozwoli nam wykorzystać informacje, które już posiadamy.
Mianowicie skorzystamy ze wzoru redukcyjnego sin(x + π/2) = = cos x. Wzór ten można rozumieć następująco: funkcja y = cos x przyjmuje takie same wartości jak funkcja y = sin x, ale wcześniej π/2. Przykładowo funkcja y = sin x przyjmuje wartość 1 przy x = π/2, a funkcja y = cos x = sin(x + π/2) przyjmuje tę samą wartość już przy x = 0. Na wykresie to oznacza: dla każdego punktu wykresu y = sin x jest punktem wykresu y = cos x, którego rzędna jest taka sama, a odcięta jest o π/2 mniejsza (rys. 11.5). Zatem wykres y = cos x otrzymamy, jeśli wykres y = sin x przesuniemy wzdłuż osi odciętych o π/2 w lewo. Na ryc. 11.5 wykres funkcji y = cos x pokazano jako krzywą ciągłą.
Odkryliśmy więc, że wykres cosinusa ulega transformacji
wywołanie (przesunięcie) z wykresu sinusoidalnego. Przypadki, w których wykres jednej funkcji można otrzymać poprzez przekształcenie z wykresu innej funkcji, są same w sobie interesujące, dlatego powiedzmy o nich kilka słów.
Na przykład, jak wyglądałby wykres funkcji y = 2 sin x? Oczywiste jest, że współrzędne punktów tego wykresu uzyskuje się ze rzędnych odpowiednich punktów wykresu y = sin x poprzez pomnożenie przez 2, tak że nasz wykres będzie przedstawiony jako pełna krzywa na ryc. 11.6. Można powiedzieć, że wykres y = 2 sin x otrzymujemy z wykresu y = sin x rozciągając go dwukrotnie wzdłuż rzędnej.
Ryż. 11.6. y = 2 grzech x. | |||
Ryż. 11.7. y = grzech 2x.
Teraz narysujmy funkcję y = sin 2x. Łatwo to zrozumieć
Ryż. 11.8. y = grzech (2x + π/3).
że funkcja y = sin 2x przyjmuje te same wartości co funkcja y = sin x, ale o połowę wartości x. Przykładowo funkcja y = sin x przyjmuje wartość 1 przy x = π/2, a funkcja y = sin 2x - już przy x = π/4; innymi słowy, aby otrzymać wykres y = sin 2x, należy podzielić o połowę odcięte wszystkich punktów wykresu y = sin x i pozostawić rzędne bez zmian. To, co się dzieje, pokazano na ryc. 11.7. Można powiedzieć, że wykres y = sin 2x (linia ciągła na ryc. 11.7) otrzymuje się z wykresu y = sin x poprzez 2-krotne skompresowanie do rzędnej.
Spróbujmy także wykreślić funkcję y = sin(2x + π/3). Oczywiste jest, że należy to uzyskać poprzez jakąś transformację z wykresu y = sin 2x. Na pierwszy rzut oka może się wydawać, że transformacja ta jest przesunięciem w lewo o π/3 wzdłuż osi x, podobnie jak pokazano na rys. 11.5. Gdyby jednak tak było, okazałoby się np., że funkcja y = sin(2x + π/3) przyjmuje wartość 1 przy x = π/4 − π/3 = π/12, co nie jest prawda (sprawdź!). Prawidłowe rozumowanie jest następujące: sin(2x + π/3) = sin 2(x + π/6), więc funkcja y = sin(2x+π/3) przyjmuje takie same wartości jak funkcja y = sin 2x , ale π/6 wcześniej. Zatem przesunięcie w lewo nie następuje o π/3, ale o π/6 (ryc. 11.8).
Krzywe będące wykresami funkcji y = a sin bx, gdzie a 6 = 0, b 6 = 0, nazywane są sinusoidami. Należy zauważyć, że nie ma potrzeby wprowadzania krzywej „cosinus”: jak widzieliśmy, wykres cosinus jest tą samą krzywą co wykres sinus, tylko jest umiejscowiony inaczej.
względem osi współrzędnych.
Zadanie 11.2. Jakie współrzędne mają punkty zaznaczone na ryc. 11,8 znaków zapytania?
Zadanie 11.3. Weź świecę, cienką kartkę papieru i ostry nóż. Owiń świecę kilkoma warstwami arkusza papieru i ostrożnie przetnij nożem świecę i papier po przekątnej. Teraz rozłóż papier. Zobaczysz, że został przecięty wzdłuż falistej linii. Udowodnić, że ta linia falista jest sinusoidą.
Zadanie 11.4. Wykres funkcji: | ||||||||||||||
d) y = 3 cos 2x; | ||||||||||||||
a) y = - grzech x; B) | c) y = cos(x/2); | |||||||||||||
g) y = sin(πx). D) | ||||||||||||||
Komentarz. Jeśli spiskujesz funkcje trygonometryczne na papierze w kratkę wygodnie jest wybrać nieco inne skale wzdłuż osi, tak aby na osi odciętych liczba π odpowiadała całkowitej liczbie komórek. Na przykład często wybiera się następującą skalę: wzdłuż osi rzędnych odcinek o długości 1 zajmuje dwie komórki; wzdłuż osi odciętych odcinek o długości π zajmuje 6 komórek.
Zadanie 11.5. Wykres funkcji:
a) y = arcsin x; b) y = arccos x.
Zobaczmy jak na wykresach wyglądają już znane rozwiązania równań sin x = a i cos x = a. Rozwiązania te są odciętymi punktów przecięcia prostej poziomej y = a z wykresem funkcji y = sin x (odpowiednio y = cos x). Na ryc. 11.9,11.10 wyraźnie widoczne są dwie serie rozwiązań otrzymanych przy -1< a < 1.
Wykresy sinusa i cosinusa pokazują, w jakich odstępach te funkcje rosną, a w jakich maleją. Widać na przykład, że funkcja y = sin x rośnie na przedziałach [−π/2; π/2],
Konwersja wykresów funkcji
W tym artykule przedstawię Państwu przekształcenia liniowe wykresów funkcyjnych oraz pokażę jak za pomocą tych przekształceń otrzymać wykres funkcji z wykresu funkcji 
Transformacja liniowa funkcji to transformacja samej funkcji i/lub jej argumentu do postaci 
, a także transformację zawierającą argument i/lub moduł funkcji.
Największe trudności przy konstruowaniu wykresów za pomocą przekształceń liniowych powodują następujące działania:
I Właśnie w tych punktach zajmiemy się bardziej szczegółowo.
Przyjrzyjmy się bliżej funkcji
Opiera się na funkcji. Zadzwońmy do niej podstawowa funkcja.
Podczas kreślenia funkcji dokonujemy przekształceń na wykresie funkcji bazowej.
Gdybyśmy mieli dokonać przekształceń funkcji wówczas w tej samej kolejności, w jakiej znaleziono jego wartość dla określonej wartości argumentu
Zastanówmy się, jakie rodzaje transformacji liniowych argumentów i funkcji istnieją i jak je wykonać.
Transformacje argumentów.
1. f(x) f(x+b)
1. Zbuduj wykres funkcji
2. Przesuń wykres funkcji wzdłuż osi OX o |b| jednostki
Narysujmy funkcję
1. Zbuduj wykres funkcji
2. Przesuń go o 2 jednostki w prawo:
2. f(x) f(kx)
1. Zbuduj wykres funkcji
2. Podziel odcięte punktów wykresu przez k, pozostawiając rzędne punktów bez zmian.
Zbudujmy wykres funkcji.
1. Zbuduj wykres funkcji
2. Podziel wszystkie odcięte punktów wykresu przez 2, pozostawiając rzędne bez zmian:
3. f(x) f(-x)
1. Zbuduj wykres funkcji
2. Wyświetl go symetrycznie względem osi OY.
Zbudujmy wykres funkcji.
1. Zbuduj wykres funkcji
2. Wyświetl go symetrycznie względem osi OY:
4. f(x) fa(|x|)
1. Zbuduj wykres funkcji
2. Wymazuje się część wykresu znajdującą się na lewo od osi OY, część wykresu znajdującą się na prawo od osi OY uzupełnia się symetrycznie względem osi OY:
Wykres funkcji wygląda następująco:
Narysujmy funkcję
1. Budujemy wykres funkcji (jest to wykres funkcji przesunięty wzdłuż osi OX o 2 jednostki w lewo):
2. Część wykresu zlokalizowana na lewo od osi OY (x).<0) стираем:
3. Uzupełniamy część wykresu znajdującą się na prawo od osi OY (x>0) symetrycznie względem osi OY:
Ważny! Dwie główne zasady przekształcania argumentu.
1. Wszystkie transformacje argumentów wykonywane są wzdłuż osi OX
2. Wszelkie przekształcenia argumentu wykonujemy „odwrotnie” i „w odwrotnej kolejności”.
Przykładowo w funkcji kolejność transformacji argumentów jest następująca:
1. Weź moduł x.
2. Dodaj liczbę 2 do modulo x.
Ale skonstruowaliśmy wykres w odwrotnej kolejności:
Najpierw wykonano transformację 2 - wykres przesunięto o 2 jednostki w lewo (czyli odcięte punktów zmniejszono o 2, jakby „na odwrót”)
Następnie wykonaliśmy transformację f(x) f(|x|).
W skrócie sekwencję przekształceń zapisuje się następująco:
Teraz porozmawiajmy o transformacja funkcji . Następują przemiany
1. Wzdłuż osi OY.
2. W tej samej kolejności, w jakiej wykonywane są czynności.
Oto przekształcenia:
1. f(x)f(x)+D
2. Przesuń go wzdłuż osi OY o |D| jednostki
Narysujmy funkcję
1. Zbuduj wykres funkcji
2. Przesuń go wzdłuż osi OY o 2 jednostki w górę:
2. f(x)Af(x)
1. Zbuduj wykres funkcji y=f(x)
2. Mnożymy rzędne wszystkich punktów wykresu przez A, pozostawiając odcięte bez zmian.
Narysujmy funkcję
1. Zbudujmy wykres funkcji
2. Pomnóż współrzędne wszystkich punktów na wykresie przez 2:
3.f(x)-f(x)
1. Zbuduj wykres funkcji y=f(x)
Zbudujmy wykres funkcji.
1. Zbuduj wykres funkcji.
2. Wyświetlamy go symetrycznie względem osi OX.
4. f(x)|f(x)|
1. Zbuduj wykres funkcji y=f(x)
2. Część wykresu znajdującą się powyżej osi OX pozostawiamy bez zmian, część wykresu znajdującą się poniżej osi OX wyświetlamy symetrycznie względem tej osi.
Narysujmy funkcję
1. Zbuduj wykres funkcji. Uzyskuje się to poprzez przesunięcie wykresu funkcji wzdłuż osi OY o 2 jednostki w dół:
2. Teraz wyświetlimy część wykresu znajdującą się poniżej osi OX symetrycznie względem tej osi:
I ostatnia transformacja, której, ściśle rzecz biorąc, nie można nazwać transformacją funkcyjną, ponieważ wynik tej transformacji nie jest już funkcją:
|y|=f(x)
1. Zbuduj wykres funkcji y=f(x)
2. Wymazujemy część wykresu znajdującą się poniżej osi OX, następnie uzupełniamy część wykresu znajdującą się powyżej osi OX symetrycznie względem tej osi.
Ułóżmy równanie
1. Budujemy wykres funkcji:
2. Usuń część wykresu znajdującą się poniżej osi OX:
3. Uzupełniamy część wykresu znajdującą się nad osią OX symetrycznie względem tej osi.
Na koniec proponuję obejrzeć TUTORIAL WIDEO, w którym pokazuję krok po kroku algorytm konstruowania wykresu funkcji
Wykres tej funkcji wygląda następująco:
Z wykresów jasno wynika, że:
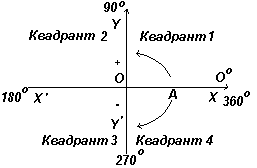Na ryc. po lewej stronie znajdują się prostopadłe osie XX” i YY”; przecinają się w początku współrzędnych O. Podczas pracy z wykresami pomiary w prawo i w górę od O są uważane za dodatnie, a w lewo i w dół od O za ujemne. Niech OA obraca się swobodnie względem O. Kiedy OA jest obracany w kierunku przeciwnym do ruchu wskazówek zegara, zmierzony kąt uważa się za dodatni, a gdy obraca się zgodnie z ruchem wskazówek zegara, jest uważany za ujemny.
Harmonogram. Pozytywne lub negatywne
kierunek podczas poruszania się po okręgu.
Niech OA obraca się w kierunku przeciwnym do ruchu wskazówek zegara w taki sposób, aby Θ 1 było dowolnym kątem w pierwszej ćwiartce i konstruuje prostopadłą AB, aby otrzymać trójkąt prostokątny OAB na ryc. lewy. Ponieważ wszystkie trzy boki trójkąta są dodatnie, funkcje trygonometryczne sinus, cosinus i tangens w pierwszej ćwiartce będą dodatnie. (Zauważ, że długość OA jest zawsze dodatnia, ponieważ jest to promień okręgu.)
Niech OA obraca się dalej w taki sposób, aby Θ 2 było dowolnym kątem w drugiej ćwiartce i konstruuje AC tak, aby powstał trójkąt prostokątny OAC. Wtedy grzech Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tan Θ 2 =+/- = -. Niech OA obraca się dalej w taki sposób, aby Θ 3 było dowolnym kątem w trzeciej ćwiartce i konstruuje AD tak, aby powstał trójkąt prostokątny OAD. Wtedy grzech Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tan Θ 3 = -/- =+ .
Niech OA obraca się dalej w taki sposób, aby Θ 4 było dowolnym kątem w czwartej ćwiartce i konstruuje AE tak, aby powstał trójkąt prostokątny OAE. Wtedy grzech Θ 4 = -/+= -; sałata Θ 4 =+/+=+; tan Θ 4 = -/+= -.
W pierwszej ćwiartce wszystkie funkcje trygonometryczne mają wartości dodatnie, w drugiej tylko sinus jest dodatni, w trzeciej tylko tangens, w czwartej tylko cosinus, jak pokazano na ryc. lewy.
Znajomość kątów o dowolnej wielkości jest konieczna przy znajdowaniu na przykład wszystkich kątów z zakresu od 0 o do 360 o, których sinus wynosi, powiedzmy, 0,3261. Jeśli wpiszemy do kalkulatora 0,3261 i wciśniemy przycisk sin -1, otrzymamy odpowiedź 19,03 o. Istnieje jednak drugi kąt pomiędzy 0 o a 360 o, którego kalkulator nie pokaże. Sinus jest również dodatni w drugiej ćwiartce. Inny kąt pokazano na ryc. poniżej jako kąt Θ, gdzie Θ=180 o - 19,03 o = 160,97 o. Zatem 19,03 o i 160,97 o to kąty z zakresu od 0 o do 360 o, których sinus wynosi 0,3261.
Bądź ostrożny! Kalkulator podaje tylko jedną z tych wartości. Drugą wartość należy wyznaczyć zgodnie z teorią kątów dowolnych.
Przykład 1
Znajdź wszystkie kąty z zakresu od 0 o do 360 o, których sinus wynosi -0,7071 
Rozwiązanie:
Kąty, których sinus wynosi -0,7071 o, znajdują się w trzeciej i czwartej ćwiartce, ponieważ sinus w tych ćwiartkach jest ujemny (patrz rysunek po lewej).
Harmonogram. Znalezienie wszystkich kątów według
podana wartość sinusa (przykład)
.gif)
Notatka. Kalkulator podaje tylko jedną odpowiedź.
Harmonogram. Znalezienie wszystkich kątów według
podana wartość sinusa (przykład)
Przykład 2
Znajdź wszystkie kąty od 0 o do 360 o, których tangens wynosi 1,327. 
Rozwiązanie:
Tangens jest dodatni w pierwszej i trzeciej ćwiartce - rys. lewy.
Harmonogram. Znalezienie wszystkich kątów według
Z poniższego rysunku Θ = arctan1,327= 53 o. .gif)
Dwa kąty z zakresu od 0 o do 360 o, których tangens wynosi 1,327, to 53 o i 180 o + 53 o, tj. 233 o.
Harmonogram. Znalezienie wszystkich kątów według
podana wartość tangensu (przykład)
Niech OR na ryc. po lewej stronie znajduje się wektor o jednostkowej długości, swobodnie obracający się wokół O w kierunku przeciwnym do ruchu wskazówek zegara. Jeden obrót tworzy okrąg pokazany na ryc. i podzielony na sektory po 15 o. Każdy promień ma składową poziomą i pionową. Na przykład dla 30 o składowa pionowa to TS, a składowa pozioma to OS. Z definicji funkcji trygonometrycznych
sin30 o =TS/TO=TS/1, tj. TS= sin30 o I cos30 o =OS/TO=OS/1, tj. OS=cos30 o
Składową pionową TS można przedstawić jako T"S", która jest równa wartości odpowiadającej kątowi 30 o na wykresie zależności y od kąta x. Jeśli wszystkie składowe pionowe, takie jak TS, przeniesiemy na wykres, otrzymamy sinusoidę pokazaną na ryc. wyższy.
 |
 |
 |
 |
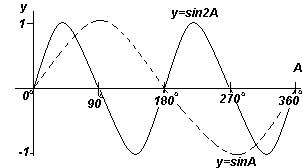Funkcje okresowe i okres
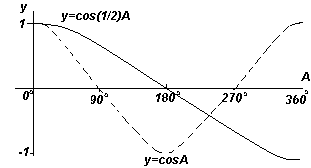
Każdy z wykresów funkcji pokazanych na czterech ryc. powyżej, powtarza się wraz ze wzrostem kąta A i dlatego są nazywane funkcje okresowe.
Funkcje y=sinA i y=cosA powtarzają się co 360 o (lub 2π radianów), zatem 360 o nazywa się okres te funkcje. Funkcje y=sin2A i y=cos2A powtarzają się co 180 o (lub π radianów), zatem 180 o jest okresem tych funkcji.
Generalnie, jeśli y=sinpA i y=cospA (gdzie p jest stałą), to okres funkcji wynosi 360 o /p (czyli 2π/p radianów). Zatem jeśli y=sin3A, to okres tej funkcji wynosi 360 o /3= 120 o, jeśli y=cos4A, to okres tej funkcji wynosi 360 o /4= 90 o.
Amplituda
Amplituda nazywa się maksymalną wartością sinusoidy. Każdy z wykresów 1-4 ma amplitudę +1 (tzn. wahają się pomiędzy +1 a -1). Jeżeli jednak y=4sinA, to każdą z wartości sinA mnoży się przez 4, więc maksymalna wartość amplitudy wynosi 4. Podobnie dla y=5cos2A amplituda wynosi 5, a okres wynosi 360 o /2 = 180 o.
Przykład 3.
Skonstruuj y=3sin2A w zakresie od A=0 o do A=360 o. 
Rozwiązanie:
Amplituda =3, okres = 360 o /2 =180 o.
Przykład 4.
Narysuj wykres y=4cos2x w zakresie od x=0 o do x=360 o 
Rozwiązanie:
Amplituda = 4. okres = 360 o /2 =180 o.
Kąty opóźnienia i wyprzedzenia
Krzywe sinus i cosinus nie zawsze zaczynają się od 0 o. Aby uwzględnić tę okoliczność, funkcję okresową przedstawia się jako y=sin(A± α), gdzie α jest przesunięciem fazowym względem y=sinA i y=cosA.
.gif)
Po skompletowaniu tabeli wartości można zbudować wykres funkcji y=sin(A-60 o), pokazany na ryc. lewy. Jeżeli krzywa y=sinA zaczyna się od 0 o, to krzywa y=sin(A-60 o) zaczyna się od 60 o (tzn. jej wartość zerowa jest przesunięta o 60 o w prawo). Mówią więc, że y=sin(A-60 o) jest późno względem y=sinA o 60 o.
Harmonogram. y=sin(A-60 o) (sinusoida).
.gif)
Po skompletowaniu tabeli wartości można zbudować wykres funkcji y=cos(A+45 o), pokazanej na ryc. poniżej.
Jeżeli krzywa y=cosA zaczyna się od 0 o, to krzywa y=cos(A+45 o) zaczyna się 45 o w lewo (tzn. jej wartość zerowa jest 45 o wcześniej).
Zatem mówimy, że wykres ma postać y=cos(A+45 o) dalej wykres y=cosA przy 45 o.
Harmonogram. y=cos(A+45 o) (fala cosinus).
Generalnie wykres y=sin(A-α) jest opóźniony względem y=sinA o kąt α.
Fala cosinus ma taki sam kształt jak fala sinusoidalna, ale zaczyna się o 90 o w lewo, tj. przed nią o 90 o. Zatem cosA=sin(A+90 o).
Przykład 5.
Narysuj wykres y=5sin(A+30 o) w przedziale od A=0 o do A=360 o
.gif)
Przykład 6.
Narysuj wykres y=7sin(2A-π/3) w przedziale od A=0 o do A=360 o.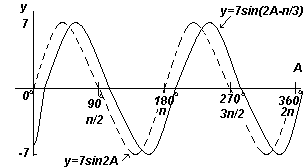 
Rozwiązanie:
Amplituda = 7, okres =2π/2= π radianów
Zazwyczaj y=sin(pt-α) jest opóźnione względem y=sinpt o α/p, dlatego 7sin(2A-π/3) pozostaje w tyle za 7sin2A o (π/3)/2, tj. o π/6 radianów lub 30 o
Sinusoida postaci Asin(ωt±α). Kąt fazowy. Przesunięcie fazowe. 
Niech OR na ryc. po lewej stronie wektor swobodnie obracający się w kierunku przeciwnym do ruchu wskazówek zegara wokół O z prędkością ω radianów/s. Nazywa się wektor obracający się wektor fazowy. Po czasie t sekund OR obróci się o kąt ωt radianów (na rysunku po lewej stronie jest to kąt TOR). Jeśli skonstruujemy ST prostopadle do OR, to sinωt=ST/OT, tj. ST=OTsinωt.
Jeśli wszystkie takie składowe pionowe zostaną rzutowane na wykres y w funkcji ωt, otrzymana zostanie sinusoida o amplitudzie OR.
Jeżeli wektor fazowy OR wykona jeden obrót (tj. 2π radianów) w T sekundach, to prędkość kątowa ω=2π/T rad/s, skąd
T=2π/ ω (s), gdzie
T jest okres
Nazywa się liczbą pełnych okresów upływających w ciągu 1 sekundy częstotliwość F.
Częstotliwość = (liczba okresów)/(sekunda) = 1/ T = ω/2π Hz, te. f= ω/2π Hz
Dlatego prędkość kątowa
ω=2πf rad/s.
Jeśli ogólnie funkcja sinusoidalna wygląda jak y=sin(ωt± α), to
A - amplituda
ω - prędkość kątowa
2π/ ω - okres T, s
ω/2π - częstotliwość f, Hz
α jest kątem wyprzedzenia lub opóźnienia (względem y=Asinωt) w radianach, nazywany jest także kątem fazowym.
Przykład 7.
Prąd przemienny wyraża się jako i=20sin(90πt+0,26) amperów. Określ amplitudę, okres, częstotliwość i kąt fazowy (w stopniach)
Rozwiązanie:
i=20sin(90πt+0,26)I dlatego
amplituda jest 20 A
prędkość kątowa ω=90π zatem,
koniec dyskusji= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
częstotliwość F= 1/T = 1/0,022 = 45,46 Hz
kąt fazowy α= 0,26 rad. = (0,26*180/π) o = 14,9 o.
Przykład 8.
Mechanizm oscylacyjny ma maksymalne przemieszczenie 3 m i częstotliwość 55 Hz. W chwili t=0 przemieszczenie wynosi 100 cm. Wyraź przemieszczenie w ogólnej formie Аsin(ωt± α).
Rozwiązanie
Amplituda = maksymalne przemieszczenie = 3 m
Prędkość kątowa ω=2πf = 2π(55) = 110 πrad/s
Zatem przemieszczenie wynosi 3sin(110πt + α)m.
Przy t=0 przemieszczenie = 100cm=1m.
Dlatego 1= 3sin(0 + α), tj. sinα=1/3=0,33
Zatem α=arcsin0,33=19 o
Zatem przesunięcie wynosi 3 sin(110 πt + 0,33).
Przykład 9.
Wartość chwilowego napięcia w obwodzie prądu przemiennego w dowolnej chwili t sekund jest podawana jako v=350sin(40πt-0,542)V. Znajdować:
a) Amplituda, okres, częstotliwość i kąt fazowy (w stopniach)
b) wartość napięcia w chwili t = 0
c) wartość napięcia w czasie t = 10 ms
d) czas, w którym napięcie po raz pierwszy osiąga 200 V. 
Rozwiązanie:
a) Amplituda wynosi 350 V, prędkość kątowa ω=40π
Stąd,
okres T=2π/ ω=2π/40π=0,05 s =50ms
częstotliwość f=1/T=1/0,05=20 Hz
kąt fazowy = 0,542 rad (0,542*180/π) = 31 o z opóźnieniem względem v=350sin(40πt)
b) Jeżeli t =0, to v=350sin(0-0,542)=350sin(-31 o)=-180,25 V
c) Jeżeli t =10 ms, to v=350sin(40π10/10 3 -0,542)=350sin(0,714)=350sin41 o =229,6 V
d) Jeżeli v=200 I, to 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)
Harmonogram. Mechanizm oscylacyjny
(na przykład sinusoida).
v=350sin(40πt-0,542) Zatem (40πt-0,542)=arcsin200/350=35 o lub 0,611 rad.
40πt= 0,611+0,542=1,153.
Zatem jeśli v=200V, to czas t=1,153/40π=9,179 ms
