
Pochodna funkcji jest jednym z trudnych tematów w program nauczania. Nie każdy absolwent odpowie na pytanie, czym jest pochodna.
Ten artykuł w prosty i jasny sposób wyjaśnia, czym jest pochodna i dlaczego jest potrzebna.. Nie będziemy teraz dążyć do matematycznego rygoru prezentacji. Najważniejszą rzeczą jest zrozumienie znaczenia.
Zapamiętajmy definicję:
Pochodna to szybkość zmiany funkcji.
Rysunek przedstawia wykresy trzech funkcji. Jak myślisz, który z nich rośnie najszybciej?
Odpowiedź jest oczywista – trzecia. Ma najwyższą stopę zmiany, czyli największą pochodną.
Oto kolejny przykład.
Kostia, Grisha i Matvey dostali pracę w tym samym czasie. Zobaczmy, jak zmieniły się ich dochody w ciągu roku:

Możesz od razu zobaczyć wszystko na wykresie, prawda? Dochody Kostii wzrosły ponad dwukrotnie w ciągu sześciu miesięcy. Dochody Grishy również wzrosły, ale tylko trochę. A dochód Mateusza spadł do zera. Warunki początkowe są takie same, ale tempo zmiany funkcji, tj. pochodna, - różne. Co do Matveya, pochodna jego dochodu jest na ogół ujemna.
Intuicyjnie możemy łatwo oszacować tempo zmian funkcji. Ale jak to robimy?
To, na co naprawdę patrzymy, to to, jak stromo rośnie (lub spada) wykres funkcji. Innymi słowy, jak szybko zmienia się y z x. Oczywiście ta sama funkcja w różnych punktach może mieć różną wartość pochodnej - to znaczy może zmieniać się szybciej lub wolniej.
Pochodna funkcji jest oznaczona przez .
Pokażmy, jak znaleźć za pomocą wykresu.

Narysowany jest wykres jakiejś funkcji. Wskaż na to punkt odciętą. Narysuj styczną do wykresu funkcji w tym miejscu. Chcemy ocenić, jak stromo rośnie wykres funkcji. Przydatną wartością tego jest tangens nachylenia stycznej.
Pochodna funkcji w punkcie jest równa tangensowi nachylenia stycznej narysowanej na wykresie funkcji w tym punkcie.
Uwaga - jako kąt nachylenia stycznej przyjmujemy kąt pomiędzy styczną a dodatnim kierunkiem osi.
Czasami uczniowie pytają, jaka jest styczna do wykresu funkcji. Jest to linia prosta, która ma jedyny wspólny punkt z wykresem w tej sekcji, co więcej, jak pokazano na naszym rysunku. Wygląda jak styczna do okręgu.
Znajdźmy . Pamiętamy, że tangens kąta ostrego w trójkąt prostokątny równy stosunkowi przeciwnej nogi do sąsiedniej. Z trójkąta:
Znaleźliśmy pochodną, korzystając z wykresu, nie znając nawet wzoru funkcji. Takie zadania często znajdują się na egzaminie z matematyki pod numerem.
Jest jeszcze jedna ważna korelacja. Przypomnijmy, że linię prostą daje równanie
Wielkość w tym równaniu nazywa się nachylenie linii prostej. Jest równy tangensowi kąta nachylenia linii prostej do osi.
.
Rozumiemy to
Zapamiętajmy tę formułę. Wyraża geometryczne znaczenie pochodnej.
Pochodna funkcji w punkcie jest równa nachyleniu stycznej narysowanej na wykresie funkcji w tym punkcie.
Innymi słowy, pochodna jest równa tangensowi nachylenia stycznej.
Powiedzieliśmy już, że ta sama funkcja może mieć różne pochodne w różnych punktach. Zobaczmy, jak pochodna jest związana z zachowaniem funkcji.
Narysujmy wykres jakiejś funkcji. Niech ta funkcja wzrośnie w niektórych obszarach, zmniejszy się w innych, a wraz z inna prędkość. I niech ta funkcja ma punkty maksymalne i minimalne.

W pewnym momencie funkcja się zwiększa. Styczna do wykresu narysowanego w postaci punktowej ostry róg; z dodatnim kierunkiem osi. Więc pochodna jest dodatnia w tym punkcie.
W tym momencie nasza funkcja maleje. Styczna w tym miejscu tworzy kąt rozwarty; z dodatnim kierunkiem osi. Od stycznej kąt rozwarty jest ujemna, pochodna jest ujemna w punkcie.
Oto, co się dzieje:
Jeśli funkcja rośnie, jej pochodna jest dodatnia.
Jeśli maleje, to jego pochodna jest ujemna.
A co się stanie na maksymalnym i minimalnym punkcie? Widzimy, że w punkcie (punkt maksymalny) i (punkt minimalny) styczna jest pozioma. Dlatego tangens nachylenia stycznej w tych punktach wynosi zero, a pochodna również wynosi zero.
Punkt jest punktem maksymalnym. W tym momencie wzrost funkcji zostaje zastąpiony spadkiem. W konsekwencji znak pochodnej zmienia się w punkcie z „plus” na „minus”.
W punkcie - punkcie minimalnym - pochodna również jest równa zeru, ale jej znak zmienia się z "minus" na "plus".
Wniosek: za pomocą pochodnej możesz dowiedzieć się wszystkiego, co nas interesuje o zachowaniu funkcji.
Jeśli pochodna jest dodatnia, funkcja rośnie.
Jeśli pochodna jest ujemna, funkcja maleje.
W punkcie maksymalnym pochodna wynosi zero i zmienia znak z plusa na minus.
W punkcie minimalnym pochodna również wynosi zero i zmienia znak z minus na plus.
Wyniki te zapisujemy w formie tabeli:
| wzrasta | maksymalny punkt | malejący | punkt minimalny | wzrasta | |
| + | 0 | - | 0 | + |
Zróbmy dwa małe wyjaśnienia. Jedna z nich będzie Ci potrzebna podczas rozwiązywania problemu. Kolejny - w pierwszym roku, z poważniejszym badaniem funkcji i pochodnych.
Możliwy jest przypadek, gdy pochodna funkcji w pewnym momencie jest równa zeru, ale funkcja nie ma w tym punkcie ani maksimum, ani minimum. To tak zwane :

W pewnym momencie styczna do wykresu jest pozioma, a pochodna wynosi zero. Jednak przed punktem funkcja wzrosła - a po punkcie nadal rośnie. Znak pochodnej nie zmienia się – pozostał dodatni, jak był.
Zdarza się też, że w punkcie maksimum lub minimum pochodna nie istnieje. Na wykresie odpowiada to ostrej przerwie, kiedy nie da się narysować stycznej w danym punkcie.

Ale jak znaleźć pochodną, jeśli funkcja jest podana nie przez wykres, ale przez formułę? W tym przypadku ma zastosowanie
Pochodna jest jednym z głównych pojęć matematyki wyższej. W tej lekcji przedstawimy tę koncepcję. Zapoznajmy się, bez ścisłych sformułowań matematycznych i dowodów.
To wprowadzenie pozwoli Ci:
Zrozumieć istotę prostych zadań z pochodną;
Pomyślnie rozwiąż te najbardziej trudne zadania;
Przygotuj się na poważniejsze lekcje na temat pochodnych.
Najpierw miła niespodzianka.
Ścisła definicja pochodnej opiera się na teorii granic, a sprawa jest dość skomplikowana. To denerwujące. Ale praktyczne zastosowanie pochodnej z reguły nie wymaga tak rozległej i głębokiej wiedzy!
Aby pomyślnie wykonać większość zadań w szkole i na uczelni, wystarczy wiedzieć tylko kilka terminów- zrozumieć zadanie i tylko kilka zasad- rozwiązać go. I to wszystko. To sprawia, że jestem szczęśliwy.
Poznamy się?)
W matematyce elementarnej jest wiele operacji matematycznych. Dodawanie, odejmowanie, mnożenie, potęgowanie, logarytm itp. Jeśli do tych operacji doda się jeszcze jedną operację, matematyka elementarna stanie się wyższa. Ta nowa operacja nazywa się różnicowanie. Definicja i znaczenie tej operacji zostaną omówione w osobnych lekcjach.
Tutaj ważne jest, aby zrozumieć, że różniczkowanie jest tylko operacją matematyczną na funkcji. Przyjmujemy dowolną funkcję i, zgodnie z pewnymi zasadami, przekształcamy ją. Rezultatem jest nowa funkcja. Ta nowa funkcja nosi nazwę: pochodna.
Różnicowanie- działanie na funkcji.
Pochodna jest wynikiem tego działania.
Tak jak na przykład suma jest wynikiem dodania. Lub prywatny jest wynikiem podziału.
Znając terminy, możesz przynajmniej zrozumieć zadania.) Sformułowanie jest następujące: znaleźć pochodną funkcji; weź pochodną; zróżnicować funkcję; obliczyć pochodną itp. To wszystko To samo. Oczywiście istnieją bardziej złożone zadania, w których znalezienie pochodnej (różnicowanie) będzie tylko jednym z etapów rozwiązania zadania.
Pochodna jest oznaczona kreską w prawym górnym rogu nad funkcją. Lubię to: y" lub f"(x) lub S”(t) itp.
czytać y skok, ef skok od x, es skok od te, dobrze rozumiesz...)
Liczba pierwsza może również oznaczać pochodną określonej funkcji, na przykład: (2x+3)", (x 3 )" , (sinx)” itp. Często pochodną oznacza się różniczkami, ale nie będziemy rozważać takiego zapisu w tej lekcji.
Załóżmy, że nauczyliśmy się rozumieć zadania. Nic nie zostało - nauczyć się je rozwiązywać.) Przypomnę jeszcze raz: znalezienie pochodnej to przekształcenie funkcji według określonych reguł. Tych zasad jest zaskakująco niewiele.
Aby znaleźć pochodną funkcji, wystarczy znać trzy rzeczy. Trzy filary, na których opiera się wszelkie zróżnicowanie. Oto trzy wieloryby:
1. Tablica instrumentów pochodnych (wzory różniczkowania).
3. Pochodna funkcji zespolonej.
Zacznijmy w kolejności. W tej lekcji rozważymy tabelę instrumentów pochodnych.
Świat ma nieskończoną liczbę funkcji. Wśród tego zestawu znajdują się funkcje, które są najważniejsze dla praktyczne zastosowanie. Te funkcje znajdują się we wszystkich prawach natury. Z tych funkcji, jak z klocków, można zbudować wszystkie inne. Ta klasa funkcji nazywa się funkcje podstawowe. To właśnie te funkcje są badane w szkole - liniowa, kwadratowa, hiperbola itp.
Zróżnicowanie funkcji „od zera”, czyli w oparciu o definicję pochodnej i teorię granic - rzecz dość czasochłonna. A matematycy to też ludzie, tak, tak!) Więc uprościli swoje życie (i nas). Obliczyli przed nami pochodne funkcji elementarnych. Rezultatem jest tabela instrumentów pochodnych, na której wszystko jest gotowe.)
Oto ta płyta dla najpopularniejszych funkcji. Lewy - elementarna funkcja, po prawej jest jego pochodna.
| Funkcjonować tak |
Pochodna funkcji y y" |
|
| 1 | C (stała) | C” = 0 |
| 2 | x | x" = 1 |
| 3 | x n (n jest dowolną liczbą) | (x n)" = nx n-1 |
| x 2 (n = 2) | (x 2)" = 2x | |
 |
||
| 4 | grzech x | (sinx)” = cosx |
| bo x | (cos x)" = - sin x | |
| tg x | ||
| ctg x | ||
| 5 | arcus sinus x |  |
| arccos x | 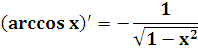 |
|
| arctg x | ||
| arcctg x | ||
| 4 | a x | |
| mi x | ||
| 5 | dziennik a x | |
| w x ( a = e) |
Polecam zwrócić uwagę na trzecią grupę funkcji w tej tabeli pochodnych. Pochodna funkcji potęgowej jest jednym z najczęstszych wzorów, jeśli nie najczęstszym! Czy wskazówka jest jasna?) Tak, dobrze jest znać na pamięć tabelę instrumentów pochodnych. Nawiasem mówiąc, nie jest to takie trudne, jak mogłoby się wydawać. Spróbuj się zdecydować więcej przykładów, sam stół zostanie zapamiętany!)
Jak rozumiesz, znalezienie wartości tabelarycznej pochodnej nie jest najtrudniejszym zadaniem. Dlatego bardzo często w takich zadaniach pojawiają się dodatkowe żetony. Albo w sformułowaniu zadania, albo w pierwotnej funkcji, której nie ma w tabeli ...
Spójrzmy na kilka przykładów:
1. Znajdź pochodną funkcji y = x 3
W tabeli nie ma takiej funkcji. Ale istnieje pochodna funkcji potęgowej w ogólny widok(trzecia grupa). W naszym przypadku n=3. Więc podstawiamy trójkę zamiast n i ostrożnie zapisujemy wynik:
(x 3) " = 3 x 3-1 = 3x 2
To wszystko.
Odpowiedź: y" = 3x 2
2. Znajdź wartość pochodnej funkcji y = sinx w punkcie x = 0.
To zadanie oznacza, że musisz najpierw znaleźć pochodną sinusa, a następnie podstawić wartość x = 0 do tej samej pochodnej. W tej kolejności! W przeciwnym razie zdarza się, że natychmiast podstawiają zero do oryginalnej funkcji ... Jesteśmy proszeni o znalezienie nie wartości oryginalnej funkcji, ale wartości jego pochodna. Pochodna, przypomnijmy, jest już nową funkcją.
Na płytce znajdujemy sinus i odpowiednią pochodną:
y" = (sinx)" = cosx
Podstaw zero do pochodnej:
y"(0) = cos 0 = 1
To będzie odpowiedź.
3. Rozróżnij funkcję:
![]()
Co inspiruje?) W tabeli derywatów nie ma nawet bliskiej takiej funkcji.
Przypomnę, że różniczkowanie funkcji to po prostu znalezienie pochodnej tej funkcji. Jeśli zapomnimy o elementarnej trygonometrii, znalezienie pochodnej naszej funkcji jest dość kłopotliwe. Stół nie pomaga...
Ale jeśli widzimy, że naszą funkcją jest cosinus podwójnego kąta, wtedy wszystko natychmiast się poprawia!
Tak tak! Pamiętaj, że przekształcenie pierwotnej funkcji przed zróżnicowaniem całkiem do przyjęcia! A to znacznie ułatwia życie. Zgodnie ze wzorem na cosinus podwójnego kąta:
![]()
Tych. nasza podstępna funkcja to nic innego jak y = cox. A to jest funkcja tabeli. Od razu otrzymujemy:
Odpowiedź: y" = - grzech x.
Przykład dla zaawansowanych absolwentów i studentów:
4. Znajdź pochodną funkcji:
Oczywiście nie ma takiej funkcji w tabeli pochodnych. Ale jeśli pamiętasz elementarną matematykę, działania z potęgami... Wtedy całkiem możliwe jest uproszczenie tej funkcji. Lubię to:

A x do potęgi jednej dziesiątej jest już funkcją tabelaryczną! Trzecia grupa, n=1/10. Bezpośrednio według wzoru i napisz:

To wszystko. To będzie odpowiedź.
Mam nadzieję, że przy pierwszym wielorybie zróżnicowania – tabeli pochodnych – wszystko jest jasne. Pozostaje zająć się dwoma pozostałymi wielorybami. W następnej lekcji poznamy zasady różnicowania.
Pierwszy poziom
Wyobraź sobie prostą drogę przechodzącą przez pagórkowaty teren. Oznacza to, że porusza się w górę iw dół, ale nie skręca w prawo ani w lewo. Jeśli oś jest skierowana poziomo wzdłuż drogi i pionowo, to linia drogi będzie bardzo podobna do wykresu jakiejś funkcji ciągłej:
Oś to pewien poziom zerowej wysokości, w życiu używamy jako niego poziomu morza.
Posuwając się do przodu taką drogą, poruszamy się również w górę lub w dół. Możemy też powiedzieć: gdy zmienia się argument (poruszanie się wzdłuż osi odciętych), zmienia się wartość funkcji (poruszanie się wzdłuż osi rzędnych). Zastanówmy się teraz, jak określić „stromo” naszej drogi? Jaka może być ta wartość? Bardzo proste: o ile zmieni się wysokość podczas poruszania się do przodu o określoną odległość. Rzeczywiście, na różnych odcinkach drogi, posuwając się do przodu (wzdłuż osi odciętej) przez jeden kilometr, wznosimy się lub opadamy o inna kwota metrów względem poziomu morza (wzdłuż osi y).
Oznaczamy postęp do przodu (czytaj „delta x”).
Grecka litera (delta) jest powszechnie używana w matematyce jako przedrostek oznaczający „zmianę”. To znaczy - to jest zmiana wielkości, - zmiana; więc co to jest? Zgadza się, zmiana rozmiaru.
Ważne: wyrażenie to pojedyncza jednostka, jedna zmienna. Nigdy nie należy odrywać „delty” od „x” ani żadnej innej litery! Czyli na przykład .
Tak więc posunęliśmy się do przodu, poziomo, dalej. Jeśli porównamy linię drogi z wykresem funkcji, to jak oznaczyć wzrost? Na pewno, . Oznacza to, że idąc naprzód, wznosimy się wyżej.
Łatwo policzyć wartość: jeśli na początku byliśmy na wysokości, a po przemieszczeniu byliśmy na wysokości, to. Jeśli punkt końcowy okazał się niższy niż punkt początkowy, będzie ujemny – oznacza to, że nie wznosimy się, ale schodzimy.

Powrót do „stromo”: jest to wartość, która wskazuje, jak bardzo (stromo) wzrasta wysokość podczas poruszania się do przodu na jednostkę odległości:
Załóżmy, że na jakimś odcinku ścieżki, posuwając się o kilometr, droga podnosi się o kilometr. Wtedy stromość w tym miejscu jest równa. A jeśli droga, posuwając się o m, zatonie o kilometr? Wtedy nachylenie jest równe.
Rozważmy teraz szczyt wzgórza. Jeśli weźmiesz początek odcinka pół kilometra do góry, a koniec pół kilometra za nim, zobaczysz, że wysokość jest prawie taka sama.

To znaczy, zgodnie z naszą logiką, okazuje się, że nachylenie tutaj jest prawie równe zeru, co oczywiście nie jest prawdą. Wiele może się zmienić w odległości kilku kilometrów. Należy wziąć pod uwagę mniejsze obszary, aby uzyskać bardziej adekwatne i dokładne oszacowanie stromości. Na przykład, jeśli zmierzysz zmianę wysokości podczas poruszania się o jeden metr, wynik będzie znacznie dokładniejszy. Ale nawet ta dokładność może nam nie wystarczyć – w końcu, jeśli na środku drogi stoi słup, możemy się przez niego po prostu prześlizgnąć. Jaką odległość zatem wybrać? Centymetr? Milimetr? Mniej znaczy lepiej!
W prawdziwe życie zmierzenie odległości z dokładnością do milimetra jest więcej niż wystarczające. Ale matematycy zawsze dążą do perfekcji. Dlatego koncepcja była: nieskończenie mały, to znaczy, że wartość modulo jest mniejsza niż jakakolwiek liczba, którą możemy nazwać. Na przykład mówisz: jeden bilionowy! O ile mniej? I dzielisz tę liczbę przez - i będzie jeszcze mniej. Itp. Jeśli chcemy napisać, że wartość jest nieskończenie mała, piszemy tak: (czytamy „x dąży do zera”). Bardzo ważne jest, aby zrozumieć że ta liczba nie jest równa zero! Ale bardzo blisko. Oznacza to, że można go podzielić na.
Pojęcie przeciwne do nieskończenie małego jest nieskończenie duże (). Prawdopodobnie już zetknąłeś się z tym, gdy pracowałeś nad nierównościami: ta liczba jest większa pod względem modułu niż jakakolwiek liczba, którą możesz wymyślić. Jeśli wymyślisz największą możliwą liczbę, po prostu pomnóż ją przez dwa, a otrzymasz jeszcze więcej. A nieskończoność to nawet więcej niż to, co się dzieje. W rzeczywistości nieskończenie duże i nieskończenie małe są odwrotne do siebie, to znaczy w i odwrotnie: w.
Teraz wróćmy na naszą drogę. Idealnie obliczone nachylenie to nachylenie obliczone dla nieskończenie małego segmentu ścieżki, czyli:
Zauważam, że przy nieskończenie małym przemieszczeniu zmiana wysokości również będzie nieskończenie mała. Ale przypomnę, że nieskończenie małe nie znaczy równe zero. Jeśli podzielisz nieskończenie małe liczby przez siebie, możesz uzyskać całkiem wspólny numer, Na przykład, . Oznacza to, że jedna mała wartość może być dokładnie dwa razy większa od innej.
Po co to wszystko? Droga, stromizna... Nie jedziemy na rajd, ale uczymy się matematyki. A w matematyce wszystko jest dokładnie takie samo, tylko inaczej nazywane.
Pochodna funkcji to stosunek przyrostu funkcji do przyrostu argumentu przy nieskończenie małym przyrostie argumentu.
Przyrost w matematyce nazywa się zmianą. Jak bardzo zmienił się argument () podczas poruszania się wzdłuż osi jest nazywany przyrost argumentów i oznaczony jako Jak bardzo zmieniła się funkcja (wysokość) podczas poruszania się do przodu wzdłuż osi o odległość jest wywoływana przyrost funkcji i jest oznaczony.
Zatem pochodną funkcji jest relacja do kiedy. Pochodną oznaczamy taką samą literą jak funkcja, tylko kreską od góry po prawej: lub po prostu. Zapiszmy więc wzór na pochodną, używając tych notacji:
Podobnie jak w analogii do drogi, tutaj, gdy funkcja rośnie, pochodna jest dodatnia, a gdy maleje, jest ujemna.
Ale czy pochodna jest równa zeru? Na pewno. Na przykład, jeśli jedziemy po płaskiej poziomej drodze, nachylenie wynosi zero. Rzeczywiście, wysokość wcale się nie zmienia. Czyli z pochodną: pochodna funkcji stałej (stałej) jest równa zeru:
ponieważ przyrost takiej funkcji wynosi zero dla każdego.
Weźmy przykład ze szczytu wzgórza. Okazało się, że można w taki sposób ułożyć końce segmentu różne strony od góry, że wysokość na końcach jest taka sama, czyli odcinek jest równoległy do osi:

Ale duże segmenty są oznaką niedokładnego pomiaru. Podniesiemy nasz odcinek równolegle do siebie, wtedy jego długość się zmniejszy.

W końcu, gdy będziemy nieskończenie blisko szczytu, długość odcinka stanie się nieskończenie mała. Ale jednocześnie pozostała równoległa do osi, to znaczy różnica wysokości na jej końcach jest równa zeru (nie ma tendencji, ale jest równa). Więc pochodna
Można to rozumieć tak: gdy stoimy na samej górze, niewielkie przesunięcie w lewo lub w prawo zmienia nasz wzrost pomijalnie.
Jest też wyjaśnienie czysto algebraiczne: po lewej stronie od góry funkcja rośnie, a po prawej maleje. Jak już wcześniej dowiedzieliśmy się, gdy funkcja rośnie, pochodna jest dodatnia, a gdy maleje, jest ujemna. Ale zmienia się płynnie, bez skoków (bo droga nie zmienia nigdzie ostro swojego nachylenia). Dlatego musi być między wartościami ujemnymi i dodatnimi. Będzie tam, gdzie funkcja ani nie wzrasta, ani nie maleje - w punkcie wierzchołka.
To samo dotyczy doliny (obszar, w którym funkcja zmniejsza się z lewej strony, a zwiększa z prawej):

Trochę więcej o przyrostach.
Więc zmieniamy argument na wartość. Z jakiej wartości się zmieniamy? Czym się teraz (argument) stał? Możemy wybrać dowolny punkt, a teraz będziemy z niego tańczyć.
Rozważ punkt ze współrzędną. Wartość funkcji w nim jest równa. Następnie robimy ten sam przyrost: zwiększamy współrzędną o. Jaki jest teraz argument? Bardzo łatwe: . Jaka jest teraz wartość funkcji? Tam, gdzie idzie argument, funkcja idzie tam: . A co z przyrostem funkcji? Nic nowego: to wciąż kwota, o jaką zmieniła się funkcja:
Przećwicz znajdowanie przyrostów:
Rozwiązania:
W różnych punktach, z tym samym przyrostem argumentu, przyrost funkcji będzie inny. Oznacza to, że pochodna w każdym punkcie ma swoją własną (o tym mówiliśmy na samym początku - stromość drogi w różnych punktach jest różna). Dlatego pisząc pochodną musimy wskazać w którym momencie:
Funkcja potęgowa nazywana jest funkcją, której argument jest do pewnego stopnia (logiczny, prawda?).
Oraz - w dowolnym zakresie: .
Najprostszy przypadek to wykładnik:
Znajdźmy jego pochodną w punkcie. Zapamiętaj definicję pochodnej:
Tak więc argument zmienia się z na. Jaki jest przyrost funkcji?
Przyrost jest. Ale funkcja w dowolnym momencie jest równa jej argumentowi. Więc:
Pochodna to:
Pochodna to:
b) Teraz rozważ funkcja kwadratowa (): .
A teraz pamiętajmy o tym. Oznacza to, że wartość przyrostu można pominąć, ponieważ jest nieskończenie mała, a więc nieistotna na tle innego wyrazu:
Mamy więc inną zasadę:
c) Kontynuujemy ciąg logiczny: .
Wyrażenie to można uprościć na różne sposoby: otwórz pierwszy nawias, korzystając ze wzoru na skrócone mnożenie sześcianu sumy, lub rozłóż całe wyrażenie na czynniki, korzystając ze wzoru na różnicę sześcianów. Spróbuj zrobić to sam w dowolny z sugerowanych sposobów.
Tak więc otrzymałem:
I znowu, pamiętaj o tym. Oznacza to, że możemy pominąć wszystkie terminy zawierające:
Otrzymujemy: .
d) Podobne zasady można uzyskać dla dużych potęg:
e) Okazuje się, że regułę tę można uogólnić na funkcję potęgową z dowolnym wykładnikiem, a nawet liczbą całkowitą:
| (2) |
Możesz sformułować regułę słowami: „stopień jest przesuwany do przodu jako współczynnik, a następnie maleje o”.
Tę zasadę udowodnimy później (prawie na samym końcu). Spójrzmy teraz na kilka przykładów. Znajdź pochodną funkcji:
Jeśli w tym momencie znowu stanie się niejasne, powtórz temat „” !!! (około stopnia ze wskaźnikiem ujemnym)
A teraz poprzez definicję (zapomniałeś już?):
;
.
Teraz jak zwykle pomijamy termin zawierający:
.
Tutaj użyjemy jednego faktu z wyższej matematyki:
Kiedy wyrażenie.
Dowód poznasz w pierwszym roku instytutu (a żeby się tam dostać, trzeba dobrze zdać egzamin). Teraz pokażę to tylko graficznie:

Widzimy, że gdy funkcja nie istnieje - punkt na wykresie jest przebijany. Ale im bliżej wartości, tym bliżej funkcji.To jest właśnie „dążenie”.
Dodatkowo możesz sprawdzić tę zasadę za pomocą kalkulatora. Tak, tak, nie wstydź się, weź kalkulator, jeszcze nie jesteśmy na egzaminie.
Więc spróbujmy: ;
Nie zapomnij przełączyć kalkulatora w tryb radianów!
itp. Widzimy, że im mniejszy, tym bliżej wartości stosunku.
a) Rozważ funkcję. Jak zwykle znajdujemy jego przyrost:
Zamieńmy różnicę sinusów w iloczyn. Aby to zrobić, używamy formuły (pamiętaj o temacie „”):.
Teraz pochodna:
Zróbmy podstawienie: . Wtedy dla nieskończenie małego jest również nieskończenie mały: . Wyrażenie for przyjmuje postać:
A teraz pamiętamy to z wyrażeniem. A także, co jeśli nieskończenie małą wartość można pominąć w sumie (to znaczy w).
Otrzymujemy więc następującą zasadę: pochodna sinusa jest równa cosinusowi:
Są to podstawowe („tablicowe”) instrumenty pochodne. Oto one na jednej liście:
Później dodamy do nich jeszcze kilka, ale te są najważniejsze, bo są najczęściej używane.
Ćwiczyć:
Rozwiązania:
Ok, masz rację, nadal nie wiemy, jak znaleźć takie pochodne. Tutaj mamy kombinację kilku rodzajów funkcji. Aby z nimi pracować, musisz nauczyć się kilku dodatkowych zasad:
W matematyce istnieje taka funkcja, której pochodna dla każdego jest równa wartości samej funkcji dla tego samego. Nazywa się „wykładnikiem” i jest funkcją wykładniczą
Podstawą tej funkcji jest stała - jest nieskończona dziesiętny, czyli liczba niewymierna (taka jak). Nazywa się ją „liczbą Eulera”, dlatego jest oznaczona literą.
Więc zasadą jest:
Bardzo łatwo to zapamiętać.
Cóż, nie zajdziemy daleko, od razu rozważymy funkcję odwrotną. Która funkcja jest odwrotnością funkcja wykładnicza? Logarytm:
W naszym przypadku podstawą jest liczba:
Taki logarytm (czyli logarytm z podstawą) nazywamy „naturalnym” i używamy dla niego specjalnej notacji: zamiast tego piszemy.
Co jest równe? Oczywiście, .
Pochodna logarytmu naturalnego jest również bardzo prosta:
Przykłady:
Odpowiedzi: Wystawca i naturalny logarytm- funkcje są wyjątkowo proste pod względem pochodnej. Funkcje wykładnicze i logarytmiczne o dowolnej innej podstawie będą miały inną pochodną, którą przeanalizujemy później, po przejrzeniu reguł różniczkowania.
Jakie zasady? Ponownie nowy semestr, ponownie?!...
Różnicowanie to proces znajdowania pochodnej.
Tylko i wszystko. Jakie jest inne słowo na ten proces? Not proizvodnovanie... Różniczka matematyki nazywana jest samym przyrostem funkcji przy. Termin ten pochodzi od łacińskiego różniczka - różnica. Tutaj.
Wyprowadzając wszystkie te reguły, użyjemy na przykład dwóch funkcji i. Potrzebne będą nam również formuły na ich przyrosty:
W sumie jest 5 zasad.
Jeśli - jakaś stała liczba (stała), to.
Oczywiście ta zasada działa również na różnicę: .
Udowodnijmy to. Pozwól, albo łatwiej.
Przykłady.
Znajdź pochodne funkcji:
Rozwiązania:
Tutaj wszystko jest takie samo: wprowadzamy Nowa cecha i znajdź jego przyrost:
Pochodna:
Przykłady:
Rozwiązania:
Teraz Twoja wiedza wystarczy, aby dowiedzieć się, jak znaleźć pochodną dowolnej funkcji wykładniczej, a nie tylko wykładnika (zapomniałeś jeszcze, co to jest?).
Więc gdzie jest jakaś liczba.
Znamy już pochodną funkcji, więc spróbujmy przenieść naszą funkcję do nowej bazy:
Do tego używamy prosta zasada: . Następnie:
Cóż, zadziałało. Teraz spróbuj znaleźć pochodną i nie zapomnij, że ta funkcja jest złożona.
Stało się?
Tutaj sprawdź sam:
Wzór okazał się bardzo podobny do pochodnej wykładnika: tak jak było, pojawił się tylko czynnik, który jest tylko liczbą, a nie zmienną.
Przykłady:
Znajdź pochodne funkcji:
Odpowiedzi:
To tylko liczba, której nie da się obliczyć bez kalkulatora, to znaczy nie ma sposobu, aby zapisać ją w więcej prosta forma. Dlatego zostawiamy to w tej formie w odpowiedzi.
Tutaj jest podobnie: znasz już pochodną logarytmu naturalnego:
Dlatego, aby znaleźć dowolny z logarytmu o innej podstawie, na przykład :
Musimy sprowadzić ten logarytm do podstawy. Jak zmienić podstawę logarytmu? Mam nadzieję, że pamiętasz tę formułę:
Dopiero teraz zamiast napiszemy:
Mianownik okazał się po prostu stałą (liczba stała, bez zmiennej). Pochodna jest bardzo prosta:
Pochodne funkcji wykładniczych i logarytmicznych prawie nigdy nie występują na egzaminie, ale znajomość ich nie będzie zbyteczna.
Co to jest „złożona funkcja”? Nie, to nie jest logarytm ani arcus tangens. Funkcje te mogą być trudne do zrozumienia (chociaż jeśli logarytm wydaje ci się trudny, przeczytaj temat „Logarytmy” i wszystko się ułoży), ale z matematycznego punktu widzenia słowo „złożony” nie oznacza „trudny”.
Wyobraź sobie mały przenośnik: dwie osoby siedzą i wykonują pewne czynności z niektórymi przedmiotami. Na przykład pierwszy zawija tabliczkę czekolady w opakowanie, a drugi wiąże go wstążką. Okazuje się, że taki złożony przedmiot: tabliczka czekolady owinięta i przewiązana wstążką. Aby zjeść tabliczkę czekolady, musisz zrobić coś przeciwnego w Odwrotna kolejność.
Stwórzmy podobny potok matematyczny: najpierw znajdziemy cosinus liczby, a następnie podniesiemy wynik do kwadratu. Więc dają nam numer (czekolada), ja znajduję jego cosinus (opakowanie), a potem podbijasz to, co mam (wiążę wstążką). Co się stało? Funkcjonować. Oto przykład funkcji złożonej: gdy, aby znaleźć jej wartość, wykonujemy pierwszą akcję bezpośrednio ze zmienną, a następnie drugą akcję z tym, co się stało w wyniku pierwszej.
Równie dobrze możemy wykonać te same czynności w odwrotnej kolejności: najpierw do kwadratu, a potem szukam cosinusa otrzymanej liczby:. Łatwo zgadnąć, że wynik prawie zawsze będzie inny. Ważna funkcja złożone funkcje: kiedy zmieniasz kolejność działań, zmienia się funkcja.
Innymi słowy, Funkcja złożona to funkcja, której argumentem jest inna funkcja: .
W pierwszym przykładzie .
Drugi przykład: (to samo). .
Ostatnia akcja, którą wykonamy, zostanie nazwana funkcja „zewnętrzna”, a czynność wykonywana jako pierwsza - odpowiednio funkcja „wewnętrzna”(są to nieformalne nazwy, używam ich tylko do wyjaśnienia materiału prostym językiem).
Spróbuj sam ustalić, która funkcja jest zewnętrzna, a która wewnętrzna:
Odpowiedzi: Rozdzielenie funkcji wewnętrznej i zewnętrznej jest bardzo podobne do zmiany zmiennych: na przykład w funkcji
zmieniamy zmienne i otrzymujemy funkcję.
No to teraz wydobędziemy naszą czekoladę - poszukaj pochodnej. Procedura jest zawsze odwrotna: najpierw szukamy pochodnej funkcji zewnętrznej, a następnie mnożymy wynik przez pochodną funkcji wewnętrznej. W oryginalnym przykładzie wygląda to tak:
Inny przykład:
Sformułujmy więc w końcu oficjalną zasadę:
Algorytm znajdowania pochodnej funkcji zespolonej:
Wszystko wydaje się proste, prawda?
Sprawdźmy na przykładach:
Rozwiązania:
1) Wewnętrzne: ;
Zewnętrzny: ;
2) Wewnętrzne: ;
(tylko nie próbuj teraz zmniejszać! Nic nie jest wyjęte spod cosinusa, pamiętasz?)
3) Wewnętrzne: ;
Zewnętrzny: ;
Od razu widać, że istnieje tutaj trzypoziomowa funkcja złożona: w końcu jest to już złożona funkcja sama w sobie i nadal wydobywamy z niej korzeń, to znaczy wykonujemy trzecią akcję (wkładamy czekoladę do opakowania i ze wstążką w teczce). Ale nie ma się czego bać: i tak tę funkcję „rozpakujemy” w tej samej kolejności, co zwykle: od końca.
Oznacza to, że najpierw rozróżniamy pierwiastek, potem cosinus, a dopiero potem wyrażenie w nawiasie. A potem to wszystko pomnożymy.
W takich przypadkach wygodnie jest ponumerować akcje. To znaczy wyobraźmy sobie, co wiemy. W jakiej kolejności wykonamy czynności, aby obliczyć wartość tego wyrażenia? Spójrzmy na przykład:
Im później zostanie wykonana akcja, tym bardziej „zewnętrzna” będzie odpowiednia funkcja. Kolejność czynności - jak poprzednio:
Tutaj zagnieżdżenie jest ogólnie 4-poziomowe. Ustalmy kierunek działania.
1. Radykalna ekspresja. .
2. Korzeń. .
3. Zatok. .
4. Kwadrat. .
5. Łącząc to wszystko w całość:
Pochodna funkcji- stosunek przyrostu funkcji do przyrostu argumentu z nieskończenie małym przyrostem argumentu:
Podstawowe pochodne:
Zasady różnicowania:
Stała jest brana ze znaku pochodnej:
Pochodna sumy:
Produkt pochodny:
Pochodna ilorazu:
Pochodna funkcji zespolonej:
Algorytm znajdowania pochodnej funkcji zespolonej:
Definicja. Niech funkcja \(y = f(x) \) będzie zdefiniowana w pewnym przedziale zawierającym punkt \(x_0 \) wewnątrz. Zwiększmy \(\Delta x \) do argumentu, aby nie opuszczać tego przedziału. Znajdź odpowiedni przyrost funkcji \(\Delta y \) (przy przejściu z punktu \(x_0 \) do punktu \(x_0 + \Delta x \)) i ułóż relację \(\frac(\Delta y )(\Delta x) \). Jeżeli istnieje granica tej relacji w \(\Delta x \rightarrow 0 \), to wskazana granica jest nazywana funkcja pochodna\(y=f(x) \) w punkcie \(x_0 \) i oznacza \(f"(x_0) \).
$$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) = f"(x_0) $$
Symbol y jest często używany do oznaczenia pochodnej. Zauważ, że y" = f(x) jest nową funkcją, ale naturalnie powiązaną z funkcją y = f(x), zdefiniowaną we wszystkich punktach x, w których istnieje powyższa granica. Ta funkcja nazywa się tak: pochodna funkcji y \u003d f (x).
Geometryczne znaczenie pochodnej składa się z następujących elementów. Jeśli styczną, która nie jest równoległa do osi y, można narysować na wykresie funkcji y \u003d f (x) w punkcie z odciętą x \u003d a, to f (a) wyraża nachylenie stycznej:
\(k = f"(a)\)
Ponieważ \(k = tg(a) \), równość \(f"(a) = tg(a) \) jest prawdziwa.
A teraz interpretujemy definicję pochodnej w kategoriach przybliżonych równości. Niech funkcja \(y = f(x) \) ma pochodną w określonym punkcie \(x \):
$$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) = f"(x) $$
Oznacza to, że w pobliżu punktu x, przybliżona równość \(\frac(\Delta y)(\Delta x) \ok f"(x) \), tj. \(\Delta y \ok f"(x) \cdot \Deltax\). Sensowne znaczenie uzyskanej przybliżonej równości jest następujące: przyrost funkcji jest „prawie proporcjonalny” do przyrostu argumentu, a współczynnik proporcjonalności jest wartością pochodnej w danym punkcie x. Na przykład dla funkcji \(y = x^2 \) przybliżona równość \(\Delta y \ok 2x \cdot \Delta x \) jest prawdziwa. Jeśli dokładnie przeanalizujemy definicję pochodnej, odkryjemy, że zawiera ona algorytm jej znajdowania.
Sformułujmy to.
1. Napraw wartość \(x \), znajdź \(f(x) \)
2. Zwiększ \(x \) argument \(\Delta x \), przejdź do nowy punkt\(x+ \Delta x \), znajdź \(f(x+ \Delta x) \)
3. Znajdź przyrost funkcji: \(\Delta y = f(x + \Delta x) - f(x) \)
4. Skomponuj relację \(\frac(\Delta y)(\Delta x) \)
5. Oblicz $$ \lim_(\Delta x \to 0) \frac(\Delta y)(\Delta x) $$
Ta granica jest pochodną funkcji w punkcie x.
Jeśli funkcja y = f(x) ma pochodną w punkcie x, to nazywa się ją różniczkowalną w punkcie x. Nazywa się procedurę znajdowania pochodnej funkcji y \u003d f (x) różnicowanie funkcje y = f(x).
Zastanówmy się nad pytaniem: jak wiąże się ciągłość i różniczkowalność funkcji w punkcie?
Niech funkcja y = f(x) będzie różniczkowalna w punkcie x. Wtedy styczną można narysować do wykresu funkcji w punkcie M (x; f (x)) i pamiętajmy, że nachylenie stycznej jest równe f "(x). Taki wykres nie może się "łamać" w punkt M, czyli funkcja musi być ciągła w x.
To było rozumowanie „na palcach”. Przedstawmy bardziej rygorystyczny argument. Jeśli funkcja y = f(x) jest różniczkowalna w punkcie x, to przybliżona równość \(\Delta y \ok f"(x) \cdot \Delta x \) jest równa zero, wtedy \(\Delta y \ ) będzie również dążył do zera i jest to warunek ciągłości funkcji w punkcie.
Więc, jeśli funkcja jest różniczkowalna w punkcie x, to w tym punkcie jest również ciągła.
Odwrotność nie jest prawdą. Na przykład: funkcja y = |x| jest wszędzie ciągła, w szczególności w punkcie x = 0, ale styczna do wykresu funkcji w „wspólnym punkcie” (0; 0) nie istnieje. Jeśli w pewnym momencie nie da się narysować stycznej do wykresu funkcji, to w tym miejscu nie ma pochodnej.
Jeszcze jeden przykład. Funkcja \(y=\sqrt(x) \) jest ciągła na całej osi liczbowej, w tym w punkcie x = 0. A styczna do wykresu funkcji istnieje w dowolnym punkcie, w tym w punkcie x = 0 Ale w tym momencie styczna pokrywa się z osią y, to znaczy jest prostopadła do osi odciętej, jej równanie ma postać x \u003d 0. Nachylenie nie ma takiej linii, co oznacza, że \(f"(0) \) też nie istnieje
Zapoznaliśmy się więc z nową właściwością funkcji - różniczkowalnością. Jak rozpoznać, czy funkcja jest różniczkowalna z wykresu funkcji?
Odpowiedź jest właściwie podana powyżej. Jeśli w pewnym momencie można narysować styczną do wykresu funkcji, która nie jest prostopadła do osi x, to w tym momencie funkcja jest różniczkowalna. Jeżeli w pewnym momencie styczna do wykresu funkcji nie istnieje lub jest prostopadła do osi x, to w tym momencie funkcja nie jest różniczkowalna.
Operacja znajdowania pochodnej nazywa się różnicowanie. Podczas wykonywania tej operacji często trzeba pracować z ilorazami, sumami, iloczynami funkcji, a także z „funkcjami funkcji”, czyli funkcjami złożonymi. Na podstawie definicji pochodnej możemy wyprowadzić reguły różniczkowania, które ułatwiają tę pracę. Jeśli C jest liczbą stałą, a f=f(x), g=g(x) to niektóre funkcje różniczkowalne, wtedy prawdziwe są następujące zasady różnicowania:
Jeśli zastosujemy się do definicji, to pochodną funkcji w punkcie jest granica współczynnika przyrostu funkcji Δ tak do przyrostu argumentu Δ x:
Wszystko wydaje się jasne. Ale spróbuj obliczyć za pomocą tego wzoru, powiedzmy, pochodną funkcji f(x) = x 2 + (2x+ 3) · mi x grzech x. Jeśli robisz wszystko z definicji, to po kilku stronach obliczeń po prostu zaśniesz. Dlatego istnieją prostsze i skuteczniejsze sposoby.
Na początek zauważamy, że tak zwane funkcje elementarne można odróżnić od całej różnorodności funkcji. Są to stosunkowo proste wyrażenia, których pochodne od dawna są obliczane i wprowadzane do tabeli. Takie funkcje są dość łatwe do zapamiętania wraz z ich pochodnymi.
Funkcje podstawowe to wszystkie wymienione poniżej. Pochodne tych funkcji muszą być znane na pamięć. Co więcej, zapamiętanie ich nie jest trudne - dlatego są elementarne.
Tak więc pochodne funkcji elementarnych:
| Nazwać | Funkcjonować | Pochodna |
| Stały | f(x) = C, C ∈ R | 0 (tak, tak, zero!) |
| Stopień z wykładnikiem wymiernym | f(x) = x n | n · x n − 1 |
| Zatoka | f(x) = grzech x | sałata x |
| Cosinus | f(x) = cos x | − grzech x(minus sinus) |
| Tangens | f(x) = tg x | 1/cos 2 x |
| Cotangens | f(x) = ctg x | − 1/sin2 x |
| naturalny logarytm | f(x) = log x | 1/x |
| Logarytm arbitralny | f(x) = log a x | 1/(x ja a) |
| Funkcja wykładnicza | f(x) = mi x | mi x(nic się nie zmieniło) |
Jeżeli funkcja elementarna jest mnożona przez dowolną stałą, to łatwo jest również obliczyć pochodną nowej funkcji:
(C · f)’ = C · f ’.
Ogólnie ze znaku pochodnej można pobrać stałe. Na przykład:
(2x 3)' = 2 ( x 3)' = 2 3 x 2 = 6x 2 .
Oczywiście podstawowe funkcje można dodawać do siebie, mnożyć, dzielić i wiele więcej. W ten sposób pojawią się nowe funkcje, już nie bardzo elementarne, ale też różniczkowalne według określonych reguł. Zasady te omówiono poniżej.
Niech funkcje f(x) oraz g(x), których pochodne są nam znane. Na przykład możesz wziąć podstawowe funkcje omówione powyżej. Następnie możesz znaleźć pochodną sumy i różnicy tych funkcji:
Tak więc pochodna sumy (różnicy) dwóch funkcji jest równa sumie (różnicy) pochodnych. Terminów może być więcej. Na przykład, ( f + g + h)’ = f ’ + g ’ + h ’.
Ściśle mówiąc, w algebrze nie istnieje pojęcie „odejmowania”. Istnieje pojęcie „elementu negatywnego”. Dlatego różnica f − g można przepisać jako sumę f+ (−1) g, a następnie pozostaje tylko jedna formuła - pochodna sumy.
f(x) = x 2 + sinx; g(x) = x 4 + 2x 2 − 3.
Funkcjonować f(x) jest sumą dwóch funkcji elementarnych, a więc:
f ’(x) = (x 2+ grzech x)’ = (x 2)' + (grzech x)’ = 2x+ cosx;
Podobnie argumentujemy dla funkcji g(x). Tylko są już trzy wyrazy (z punktu widzenia algebry):
g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · ( x 2 + 1).
Odpowiedź:
f ’(x) = 2x+ cosx;
g ’(x) = 4x · ( x
2 + 1).
Matematyka jest nauką logiczną, więc wiele osób uważa, że jeśli pochodna sumy jest równa sumie pochodnych, to pochodna iloczynu strajk"\u003e równe iloczynowi pochodnych. Ale figi do ciebie! Pochodna produktu jest obliczana przy użyciu zupełnie innej formuły. Mianowicie:
(f · g) ’ = f ’ · g + f · g ’
Formuła jest prosta, ale często zapominana. I nie tylko uczniowie, ale także studenci. Rezultatem są niepoprawnie rozwiązane problemy.
Zadanie. Znajdź pochodne funkcji: f(x) = x 3 cox; g(x) = (x 2 + 7x− 7) · mi x .
Funkcjonować f(x) jest iloczynem dwóch funkcji elementarnych, więc wszystko jest proste:
f ’(x) = (x 3 cos x)’ = (x 3)' cos x + x 3 (cos x)’ = 3x 2 cos x + x 3 (−sin x) = x 2 (3cos x − x grzech x)
Funkcjonować g(x) pierwszy mnożnik jest nieco bardziej skomplikowany, ale ogólny schemat to się nie zmienia. Oczywiście pierwszy mnożnik funkcji g(x) jest wielomianem, a jego pochodna jest pochodną sumy. Mamy:
g ’(x) = ((x 2 + 7x− 7) · mi x)’ = (x 2 + 7x− 7)' · mi x + (x 2 + 7x− 7) ( mi x)’ = (2x+ 7) · mi x + (x 2 + 7x− 7) · mi x = mi x(2 x + 7 + x 2 + 7x −7) = (x 2 + 9x) · mi x = x(x+ 9) · mi x .
Odpowiedź:
f ’(x) = x 2 (3cos x − x grzech x);
g ’(x) = x(x+ 9) · mi
x
.
Zauważ, że w ostatnim kroku pochodna jest faktoryzowana. Formalnie nie jest to konieczne, ale większość pochodnych nie jest obliczana samodzielnie, ale w celu zbadania funkcji. Oznacza to, że dalej pochodna będzie równa zeru, jej znaki zostaną znalezione i tak dalej. W takim przypadku lepiej jest rozłożyć wyrażenie na czynniki.
Jeśli istnieją dwie funkcje f(x) oraz g(x), oraz g(x) ≠ 0 na interesującym nas zbiorze możemy zdefiniować nową funkcję h(x) = f(x)/g(x). Dla takiej funkcji możesz również znaleźć pochodną:
Nie słaby, prawda? Skąd wziął się minus? Czemu g 2? Ale tak! To jeden z najbardziej złożone formuły Nie możesz tego rozgryźć bez butelki. Dlatego lepiej go przestudiować konkretne przykłady.
Zadanie. Znajdź pochodne funkcji:
W liczniku i mianowniku każdego ułamka są funkcje elementarne, więc wystarczy nam wzór na pochodną ilorazu:
Tradycyjnie dzielimy licznik na czynniki - to znacznie uprości odpowiedź:
Funkcja złożona niekoniecznie musi być formułą o długości pół kilometra. Na przykład wystarczy przyjąć funkcję f(x) = grzech x i zastąp zmienną x, powiedzmy, wł. x 2+ln x. Okazuje się f(x) = grzech ( x 2+ln x) jest funkcją złożoną. Ma też pochodną, ale nie uda się jej znaleźć zgodnie z zasadami omówionymi powyżej.
Jak być? W takich przypadkach zastąpienie zmiennej i wzór na pochodną funkcji zespolonej pomaga:
f ’(x) = f ’(t) · t', jeśli x jest zastąpiony przez t(x).
Z reguły sytuacja przy zrozumieniu tego wzoru jest jeszcze bardziej smutna niż przy pochodnej ilorazu. Dlatego lepiej też wyjaśnić to konkretnymi przykładami, z szczegółowy opis każdy krok.
Zadanie. Znajdź pochodne funkcji: f(x) = mi 2x + 3 ; g(x) = grzech ( x 2+ln x)
Zwróć uwagę, że jeśli w funkcji f(x) zamiast wyrażenia 2 x+ 3 będzie łatwe x, to otrzymujemy funkcję elementarną f(x) = mi x. Dlatego dokonujemy podstawienia: niech 2 x + 3 = t, f(x) = f(t) = mi t. Szukamy pochodnej funkcji zespolonej według wzoru:
f ’(x) = f ’(t) · t ’ = (mi t)’ · t ’ = mi t · t ’
A teraz - uwaga! Wykonywanie zamiany odwrotnej: t = 2x+ 3. Otrzymujemy:
f ’(x) = mi t · t ’ = mi 2x+ 3 (2 x + 3)’ = mi 2x+ 3 2 = 2 mi 2x + 3
Spójrzmy teraz na funkcję g(x). Oczywiście wymaga wymiany. x 2+ln x = t. Mamy:
g ’(x) = g ’(t) · t' = (grzech t)’ · t' = cos t · t ’
Wymiana odwrotna: t = x 2+ln x. Następnie:
g ’(x) = bo ( x 2+ln x) · ( x 2+ln x)' = cos ( x 2+ln x) · (2 x + 1/x).
To wszystko! Jak widać z ostatnie wyrażenie, cały problem sprowadzał się do obliczenia pochodnej sumy.
Odpowiedź:
f ’(x) = 2 mi
2x + 3 ;
g ’(x) = (2x + 1/x) co ( x 2+ln x).
Bardzo często na moich lekcjach zamiast terminu „pochodna” używam słowa „udar”. Na przykład uderzenie z sumy jest równa sumie uderzeń. Czy to jest jaśniejsze? Cóż, to dobrze.
Zatem obliczenie pochodnej sprowadza się do pozbycia się tych samych uderzeń zgodnie z omówionymi powyżej regułami. Jako ostatni przykład wróćmy do potęgi pochodnej z wykładnikiem wymiernym:
(x n)’ = n · x n − 1
Niewielu wie o tym w roli n może być liczbą ułamkową. Na przykład korzeń to x 0,5 . Ale co, jeśli pod korzeniem jest coś podstępnego? Znowu okaże się złożona funkcja - lubią dawać takie konstrukcje praca kontrolna i egzaminy.
Zadanie. Znajdź pochodną funkcji:
Najpierw przepiszmy pierwiastek jako potęgę z wykładnikiem wymiernym:
f(x) = (x 2 + 8x − 7) 0,5 .
Teraz dokonujemy podstawienia: niech x 2 + 8x − 7 = t. Znajdujemy pochodną według wzoru:
f ’(x) = f ’(t) · t ’ = (t 0,5)' t' = 0,5 t−0,5 t ’.
Dokonujemy zamiany odwrotnej: t = x 2 + 8x− 7. Mamy:
f ’(x) = 0,5 ( x 2 + 8x− 7) −0,5 ( x 2 + 8x− 7)' = 0,5 (2 x+ 8) ( x 2 + 8x − 7) −0,5 .
Na koniec wróćmy do korzeni: